File:Critical Orbit 0;3,2,1000,1....png
Page contents not supported in other languages.
Tools
General
Sister projects
In other projects
Appearance

Size of this preview: 600 × 600 pixels. Other resolutions: 240 × 240 pixels | 480 × 480 pixels.
Original file (800 × 800 pixels, file size: 24 KB, MIME type: image/png)
|
|
This is a file from the Wikimedia Commons |
Summary
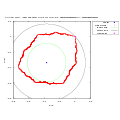
| DescriptionCritical Orbit 0;3,2,1000,1....png |
English: Critical Orbit, Inner and outer circle of Julia set for fc(z)=z*z+c where rotation number has continued fraction expansion [0;3,2,1000,1...] |
| Date | |
| Source |
own work with help and inspiration of many great people. See code nad ref This plot was created with Gnuplot by n. |
| Author | Adam majewski |
See also
-
Julia set, see also long description
-
Critical Orbit, Inner and outer circle for Golden Mean Quadratic Julia set
-
Critical orbit tends to period 3 orbit
-
3D view of critical orbit tending to parabolic fixed point
-
distance between points of critical orbit in case of attracting fixed point
-
Parabolic case
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Maxima CAS source code
/*
Computes and draw :
- period 7 indifferent orbit z: z=f^n(z)
- critical orbit
- center , inner and outer circle of critical orbit
for complex quadratic polynomial : f(z)=z*z+c
batch script for Maxima CAS
Adam Majewski 20090604- 20111124 fraktal.republika.pl
Maxima CAS ver 5.25.1
Lisp:SBCL 1.0.29.11
G N U P L O T Version 4.2 patchlevel 6
Linux 2.6.32-35-generic
*/
kill(all)$
/* basic funtion = monic and centered complex quadratic polynomial
http://en.wikipedia.org/wiki/Complex_quadratic_polynomial
*/
f(z,c):= z*z+c $
/* iterated function */
fn(n, z, c) :=
if n=1 then f(z,c)
else f(fn(n-1, z, c),c) $
/* roots of Fn are periodic point of fn function */
Fn(n,z,c):=fn(n, z, c)-z $
/* gives irreducible divisors of polynomial Fn[p,z,c]
which roots are periodic points of period p */
G[p,z,c]:=
block(
[f:divisors(p),t:1],
g,
f:delete(p,f),
if p=1
then return(Fn(p,z,c)),
for i in f do t:t*G[i,z,c],
g: Fn(p,z,c)/t,
return(ratsimp(g))
)$
/* use :
load(cpoly);
roots:GiveRoots_bf(G[3,z,c]);
this is 1-st function without fpprec
so it gives bad roots for period 8
*/
GiveRoots_bf(g):=
block(
[cc:bfallroots(expand(g)=0)],
cc:map(rhs,cc),/* remove string "c=" */
return(cc)
)$
GiveRoots_P_bf(p,c):=
block(
[g,
cc:[]],
fpprintprec:10, /* number of digits to display */
if p<7 then fpprec:16
elseif p=7 then fpprec:40
elseif p=8 then fpprec:70
elseif p=9 then fpprec:150
elseif p=10 then fpprec:300,
g:G[p,z,'c], /* here should be c as a symbol not a value */
cc:bfallroots(expand(ev(g))=0), /* ev puts value instead of c symbol */
cc:map(rhs,cc),/* remove string "c=" */
return(cc)
)$
GiveCriticalOrbit(c,iMax):=
/*
computes (without escape test)
critical orbit (forward orbit of critical point )
and saves it to the list */
block(
[z,orbit],
z:0, /* first point = critical point z:0+0*%i */
orbit:[z],
for i:1 thru iMax step 1 do
( z:expand(f(z,c)),
orbit:endcons(z,orbit),
disp(i)), /* progress info */
return(orbit)
)$
/* find fixed point alfa */
GiveFixed(c):= float(rectform((1-sqrt(1-4*c))/2))$
/* distance between point z and fixed point zf */
GiveDistanceFromCenterTo(z):= abs(z-zf)$
/*
inner radius of Siegel Disc = radius of inner circle
inner circle with center at fixed point
is the biggest circle inside Siegel Disc
criticla orbit is a boundary of SD
*/
GiveInnerRadiusOf(orbit):=lmin(map(GiveDistanceFromCenterTo,orbit))$
/* outer radius of Siegel Disc = radius of outer circle
outer circle with center at fixed point
is minimal circle containing SD
*/
GiveOuterRadiusOf(orbit):=lmax(map(GiveDistanceFromCenterTo,orbit))$
/* -------------- main ----------------- */
load(cpoly)$
compile(all)$ /* compile all functions for speed */
a:[]$ /* list for periodic points */
p:7$ /* period of z-cycle */
/* Nr of points of critical orbit to draw
To big last to long
to small gives not good image */
NrPoints:400000;
define(m(z),diff(fn(p,z,c),z,1))$ /* multiplier */
c:0.113891513213121 +0.595978335936124*%i $ /* put a value to a symbol here */
/* find periodic points */
roots[p]:GiveRoots_P_bf(p,c)$ /* ev puts value instead of c symbol */
/* find and display only indifferent */
for z in roots[p] do
(
stability:cabs(float(m(z))),
if (stability < 1.0001) and (stability> 0.0009) then /* for indifferent */
(a:cons(z,a),
disp(concat( "z=",string(float(z)),"; abs(multiplier(z))=",string(stability) ) ))
);
zf:GiveFixed(c); /* fixed point = center of Siegel disc */
zfx:realpart(zf)$
zfy:imagpart(zf)$
orbit:GiveCriticalOrbit(c,NrPoints)$
innerRadius: GiveInnerRadiusOf(orbit) ;
ir2 : innerRadius * innerRadius $
outerRadius: GiveOuterRadiusOf(orbit) ;
or2 : outerRadius * outerRadius $
/* --------------------------- draw ---------------------------------*/
load(draw); /* draw package Mario Rodriguez Riotorto
riotorto.users.sourceforge.net/gnuplot/ */
draw2d(
title= concat("Critical orbit for fc(z)=z*z + ", string(c)),
user_preamble = "set size ratio 1; set key outside right; set key box ", /* */
file_name = "cro_321d",
terminal = png,
yrange = [-0.1,1.1],
xrange = [-0.7,0.5],
dimensions = [800,800],
xlabel = "Z.re ",
ylabel = "Z.im",
point_type = filled_circle,
points_joined = false,
ip_grid = [400,400], /* Number of initial grid points in implicit plots */
key = "center ",
color =blue,
point_size = 0.9,
points([[realpart(zf),imagpart(zf)]]),
key = "inner circle",
point_size = 0.3,
color = black,
implicit( (x-zfx)^2+(y-zfy)^2 = ir2 , x,-2,2,y,-2,2),
key = "outer circle",
color = green,
implicit( (x-zfx)^2+(y-zfy)^2 = or2 , x,-2,2,y,-2,2),
key = "crital point ",
color = red ,
point_size = 1.2,
points([[0,0]]),
key = "crital value ",
color = black ,
point_size = 1.2,
points([[realpart(c),imagpart(c)]]),
key = "period 7 orbit",
color = magenta,
point_size = 1.2,
points(map(realpart,a),map(imagpart,a)),
key = "critical orbit",
color = red,
point_size = 0.3,
points(map(realpart,orbit),map(imagpart,orbit))
);
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
some value
21 November 2011
image/png
65564b10e62362f042261ff5dbc0c0e805916da8
24,580 byte
800 pixel
800 pixel
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 21:24, 25 November 2011 |  | 800 × 800 (24 KB) | Soul windsurfer | critical value over critical orbit |
| 21:08, 25 November 2011 |  | 800 × 800 (24 KB) | Soul windsurfer | added period 7 orbit and critical value | |
| 16:07, 21 November 2011 |  | 800 × 800 (23 KB) | Soul windsurfer |
File usage
The following 3 pages use this file: