File:Demj6.png
Page contents not supported in other languages.
Tools
General
Sister projects
In other projects
Appearance
Size of this preview: 600 × 600 pixels. Other resolutions: 240 × 240 pixels | 480 × 480 pixels | 1,000 × 1,000 pixels.
Original file (1,000 × 1,000 pixels, file size: 128 KB, MIME type: image/png)
|
|
This is a file from the Wikimedia Commons |
Summary
| DescriptionDemj6.png |
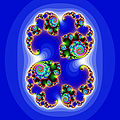
English: Imploded cauliflower : Julia set for fc(z) = z * z + 0.255 ( outside of Mandelbrot set). Sescription from program Mandel by Wolf Jung ( demo 2 page 9 ) : " Here the critical orbit escapes to infinity along the external ray 0/1. The Fatou coordinates are two partial conjugations to a translation at ∞, which show that for c = 0.25 + ε with small ε > 0, an orbit will take approximately n ≈ π/√ε iterations to pass through between the two fixed points. E.g., this explains Bott's observation that the escape time of the critical orbit for c = 0.2501 , c = 0.250001 ... is approximately 100π, 1000π ... The right image shows the "imploded cauliflower" for c = 0.251 . " |
| Date | |
| Source | Own work |
| Author | Adam majewski |
Compare with similar images
- Images for c outside Mandelbrot set
-
c = 0.28 + 0i
-
c = 0.285
-
C = 0.285 + 0.01i
-
C = 0.285 + 0.01i
-
C = 0.285 + 0.01 i
-
C = 0.285 + 0.013 i
-
c=0.45+0.1428i
- Images of Julia set for c on boundary of Mandelbrot set
-
c = 1/4 = 0.25
-
c = 0.25
-
c= 1/4 = 0.25
- circle to cauliflower to imploded cauliflower
Src code
/*
c console program:
1. draws Julia setfor Fc(z)=z*z +c
using DEM/J algorithm ( Distance Esthimation Method for Julia set )
-------------------------------
2. technic of creating ppm file is based on the code of Claudio Rocchini
http://en.wikipedia.org/wiki/Image:Color_complex_plot.jpg
create 24 bit color graphic file , portable pixmap file = PPM
see http://en.wikipedia.org/wiki/Portable_pixmap
to see the file use external application ( graphic viewer)
---------------------------------
I think that creating graphic can't be simpler
comments : Adam Majewski
gcc e.c -lm
it creates a.out file. Then run it :
./a.out
*/
#include <stdio.h>
#include <math.h>
int GiveLastIteration(double Zx, double Zy, double Cx, double Cy, int IterationMax, int ER2)
{
double Zx2, Zy2; /* Zx2=Zx*Zx; Zy2=Zy*Zy */
int i=0;
Zx2=Zx*Zx;
Zy2=Zy*Zy;
while (i<IterationMax && (Zx2+Zy2<ER2) ) /* abs(z)< ER ; ER2=ER*ER */
{
Zy=2*Zx*Zy + Cy; /* z(n+1) = zn * zn + c */
Zx=Zx2-Zy2 +Cx;
Zx2=Zx*Zx;
Zy2=Zy*Zy;
i+=1;
}
return i;
}
/*
estimates distance from point c to nearest point in Julia set
for Fc(z)= z*z + c
z(n+1) = Fc(zn)
this function is based on function mndlbrot::dist from mndlbrot.cpp
from program mandel by Wolf Jung (GNU GPL )
http://www.mndynamics.com/indexp.html
Hyunsuk Kim :
For Julia sets, z is the variable and c is a constant. Therefore df[n+1](z)/dz = 2*f[n]*f'[n] -- you don't add 1.
For the Mandelbrot set on the parameter plane, you start at z=0 and c becomes the variable. df[n+1](c)/dc = 2*f[n]*f'[n] + 1.
*/
double jdist(double Zx, double Zy, double Cx, double Cy , int iter_max)
{
int i;
double x = Zx, /* Z = x+y*i */
y = Zy,
/* Zp = xp+yp*1 = 1 */
xp = 1,
yp = 0,
/* temporary */
nz,
nzp,
/* a = abs(z) */
a;
for (i = 1; i <= iter_max; i++)
{ /* first derivative zp = 2*z*zp = xp + yp*i; */
nz = 2*(x*xp - y*yp) ;
yp = 2*(x*yp + y*xp);
xp = nz;
/* z = z*z + c = x+y*i */
nz = x*x - y*y + Cx;
y = 2*x*y + Cy;
x = nz;
/* */
nz = x*x + y*y;
nzp = xp*xp + yp*yp;
if (nzp > 1e60 || nz > 1e60) break;
}
a=sqrt(nz);
/* distance = 2 * |Zn| * log|Zn| / |dZn| */
return 2* a*log(a)/sqrt(nzp);
}
/* ------------------------------------------------------*/
int main(void)
{
const double Cx=0.255;
const double Cy=0.0;
/* screen ( integer) coordinate */
int iX,iY;
const int iXmax = 10000;
const int iYmax = 10000;
/* world ( double) coordinate = parameter plane*/
const double ZxMin=-1.25;
const double ZxMax=1.25;
const double ZyMin=-1.25;
const double ZyMax=1.25;
/* */
double PixelWidth=(ZxMax-ZxMin)/iXmax;
double PixelHeight=(ZyMax-ZyMin)/iYmax;
/* color component ( R or G or B) is coded from 0 to 255 */
/* it is 24 bit color RGB file */
const int MaxColorComponentValue=255;
FILE * fp;
char *filename="demj6.ppm";
char *comment="# ";/* comment should start with # */
static unsigned char color[3];
double Z0x, Z0y; /* Z0 = Z0x + Z0y*i */
/* */
const int IterationMax=2000;
int LastIteration;
/* bail-out value , radius of circle ; */
const int EscapeRadius=400;
int ER2=EscapeRadius*EscapeRadius;
double distanceMax=PixelWidth*6; /* /* width of boundary is related with pixel width */
/*create new file,give it a name and open it in binary mode */
fp= fopen(filename,"wb"); /* b - binary mode */
/*write ASCII header to the file*/
fprintf(fp,"P6\n %s\n %d\n %d\n %d\n",comment,iXmax,iYmax,MaxColorComponentValue);
/* compute and write image data bytes to the file*/
for(iY=0;iY<iYmax;++iY)
{
Z0y=ZyMax - iY*PixelHeight; /* reverse Y axis */
if (fabs(Z0y)<PixelHeight/2) Z0y=0.0; /* */
for(iX=0;iX<iXmax;++iX)
{ /* initial value of orbit Z0 */
Z0x=ZxMin + iX*PixelWidth;
LastIteration = GiveLastIteration( Z0x,Z0y, Cx,Cy,IterationMax, ER2);
/* compute pixel color (24 bit = 3 bytes) */
if (LastIteration == IterationMax)
{ /* interior of Julia set = black */
color[0]=0;
color[1]=0;
color[2]=0;
}
else /* exterior of Filled-in Julia set = */
{ double distance=jdist(Z0x,Z0y,Cx,Cy,IterationMax);
if (distance<distanceMax)
{ /* Julia set = white */
color[0]=255; /* Red*/
color[1]=255; /* Green */
color[2]=255;/* Blue */
}
else
{ /* exterior of Julia set = black */
color[0]=0;
color[1]=0;
color[2]=0;
};
}
/* check the orientation of Z-plane */
/* mark first quadrant of cartesian plane*/
/* if (Z0x>0 && Z0y>0) color[0]=255-color[0]; */
/*write color to the file*/
fwrite(color,1,3,fp);
}
}
fclose(fp);
printf("file saved %s \n ", filename);
getchar();
return 0;
}
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
some value
4 June 2011
130,746 byte
1,000 pixel
1,000 pixel
image/png
0f823efcefed26e142d3d27077833d7ae21e5a77
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 21:00, 4 June 2011 |  | 1,000 × 1,000 (128 KB) | Soul windsurfer |
File usage
The following 4 pages use this file:
Retrieved from "https://en.wikibooks.org/wiki/File:Demj6.png"