Fundamentals of data structures: Hashing

Hashing involves applying a hashing algorithm to a data item, known as the hashing key, to create a hash value. Hashing algorithms take a large range of values (such as all possible strings or all possible files) and map them onto a smaller set of values (such as a 128 bit number).

Hashing has two main applications. Hashed values can be used to speed data retrieval, and can be used to check the validity of data.

When we want to retrieve one record from many in a file, searching the file for the required record takes time that varies with the number of records. If we can generate a hash for the record's key, we can use that hash value as the "address" of the record and move directly to it; this takes the same time regardless of the number of records in the file.

The validity of data can be checked with a hash. This can be used to check both that a file transferred correctly, and that a file has not been deliberately manipulated by someone between me uploading it somewhere and you downloading it. If I post both the file and the hash value I generated from it, you can generate a hash value from the file you received and compare the hash values. If the hashing algorithm is a good cryptographic hash, it's extremely unlikely that accident or malice would have modified the file even a little yet it would still yield the same hash value.

Hashing tables

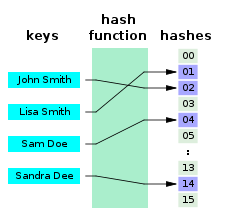
To build a set of hashing values we use a hashing algorithm to create a hashing table. Take a look at the diagram below, by applying a hashing algorithm each data item (or hashing key) has a hashing value.

A minimal perfect hash function for the four names shown

Now if we decided to search for:

Hash Key	Hashing Function	Hash Value
"Sam Doe"	Apply Hashing Function	Hash Value=3

We could search the hashing table for hashing value 3, and if we found it we would know that Sam Doe does exist.

But what about searching for an item that doesn't exist? Take a look at this example:

Hash Key	Hashing Function	Hash Value
"John Thompson"	Apply Hashing Function	Hash Value=9

We can now search the hashing table and can see that there is no entry for Hash Value=9, therefore that data doesn't exist and we didn't have to search through all the data to prove this.

Hashing Algorithms

A hash is supposed to be repeatable, that means each time we apply it to the same data we should get the same hash value out. This requires that we create a hashing algorithm or function:

Take a look at this (if you've forgotten how MOD works, go check it out!)

hashKey MOD 6

If we apply this to the following list of hash keys:

Hash Key	Hashing Algorithm	Hashing Value
12345	12345 MOD 6	3
67564	67564 MOD 6	4
34237	34237 MOD 6	1
23423	23423 MOD 6	5
00332	00332 MOD 6	2

Once we have calculated the Hash Values we can start to build the Hashing Table, notice because we are using MOD 6 we have 6 different possible Hashing Values:

Hashing Value	Hashing Key
0
1	34237
2	00332
3	12345
4	67564
5	23423

Now if you were asked whether the hashing key 23448 was a member of the data you have been given you would do the following:

1. Use the Hashing Key, apply the hashing algorithm and calculate the hashing value
2. Check for the hashing value in the hashing table
3. If it exists, you have found the data, if it doesn't the data isn't there

23448 MOD 6 = 0
Nothing attached to 0 in the hashing table
Therefore 23448 isn't stored

Exercise: Hashing tables Create a hashing table for the following hashing keys and hashing algorithm: HashKey MOD 8 Hashing Key 0353 8996 2530 6413 9119 3931 Answer: Hashing Value Hashing Key 0 1 0353 2 2530 3 3931 4 8996 5 6413 6 7 9119 Create a hashing table for the following hashing keys and hashing algorithm: (HashKey + 12) MOD 8 Hashing Key 12345 04187 34237 23423 00324 23448 Answer: Hashing Value Hashing Key 0 00324 1 34237 2 3 23423 4 23448 5 12345 6 7 04187 Can you find the hashing key 3245 stored in the following hashing table, built on the hashing algorithm: ((HashKey + 67)) MOD 8: Hashing Value Hashing Key 0 1 3... 2 3 3... 4 3... 5 2... 6 7 3... Answer: No. As (3245 + 67) MOD 8 = 0, and there is no data stored against that key in the Hashing Table Describe the following: Hashing Key Hashing Algorithm Hashing Value Answer: The hashing key is the raw data in which to be hashed. The hashing algorithm is the algorithm which performs a function to convert the hash key to the hash value. the hash value is what is produced as a result of the hash key being passed into the hashing algorithm. Describe how you create a hashing table Answer: A hashing table is made up of all of the ordered hash values and the information corresponding to it. Explain how you using hashed values to check if something exists: Answer: Hash values are used to check if something exists, as the data can be re hashed and then the hash table can be queried, this is more useful than searching for the text as computers are quicker at searching for numbers rather than text.

Collisions

Collision - When two or more hash keys result in the same hash value

Perfect Hashing	Colliding Keys
A perfect hash function for the four names shown	A hash function that maps names to integers from 0 to 15.. There is a collision between keys "John Smith" and "Sandra Dee".

You might have already noticed this, what happens when we run out of unique hashing values, when two hashing keys give the same hashing value? Take a look at the final row of the following example, built on the hashing algorithm of HashKey MOD 6:

Hash Key	Hashing Algorithm	Hashing Value
12345	12345 MOD 6	3
67564	67564 MOD 6	4
34237	34237 MOD 6	1
23423	23423 MOD 6	5
00332	00332 MOD 6	2
00338	00338 MOD 6	2 !!! Collision!

When two hash keys result in the same hash value this is called a Collision. This causes a problem as we can no longer quickly find whether data is in our hashing table or not, as another piece of data might have the same hashing value. There are several ways of solving this, we are going to look at two:

Closed Hashing (Open Addressing)

Hash collision resolved by open addressing with linear probing (interval=1). Note that "Ted Baker" has a unique hash, but nevertheless collided with "Sandra Dee" that had previously collided with "John Smith".

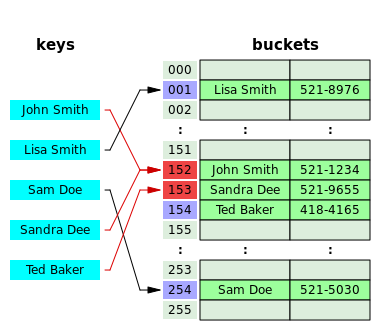
When two hash keys create the same hash value we place the colliding keys in next free hash value.

Open Hashing (Closed Addressing)

Hash collision by separate chaining with head records in the bucket array.

When two hash keys create the same hash value we place the colliding keys in the same location, by utilising a linked list to link together all the values that match that hashing value.

Uses of Hashing

Sending files

MD5

MD5("The quick brown fox jumps over the lazy dog")
= 9e107d9d372bb6826bd81d3542a419d6

Even a small change in the message will (with overwhelming probability) result in a mostly different hash:

MD5("The quick brown fox jumps over the lazy dog.")
= e4d909c290d0fb1ca068ffaddf22cbd0

Passwords

Some companies don't hash passwords, meaning that if a cracker gets into their system they can steal them. This is particularly bad when a user has the same password for multiple sites!

By hashing a password a company protects user information. Even if a cracker breaks in they don't have access to the plain text password.

When a user logs in the company doesn't store the plain text password anywhere (the hash key) , all they need is the hash value. This can then be used to see if the password is correct. The wrong password would produce a wrong hash value and the user wouldn't be allowed to log in.NOTE: This assumes a perfect hash function, so each key produces a unique value

Searching

As you should know from studying databases we often have to search for data in tables using the primary key. That is the unique value that is stored about each record. This is normally a number, but if we didn't have a numeric primary key we still need to be able to search through the data. For example the table below shows details about some students in a class, and we are going to search on the name of each student:

Name	Date of Birth	Hair Colour
John Smith	19072000	Brown
Lisa Smith	07031999	Red
Sam Doe	12121954	Blonde
Sandra Dee	01012006	Blonde
Aubrey Carringtoe	12101967	Blonde
Aubrey Carring	22102000	Black
Aubrey Carrington	22102000	Blonde
Aubrey Carringy	31092007	None
Aubrey Carringtone	04042004	Blonde
...	...	...

Searching on the name of each student could take some time as we might be searching for:

Anthony Tarkovsky

This might take checking thousands of different records and 17 characters before we were sure that we found them. If the data was even larger it could take much longer than that. What is needed is a quick way to apply an index key to each data item so we can quickly search through the data. Attaching an index key to each data item (or hashing key) is called hashing and the index value is called the hashing value. This hashing value isn't random, but is dependent on the hashing key being hashed, so that each time you apply the same hashing algorithm to the same data, you'll get the same hash value.

For example, if we hashed each name (or hash key) and we got that Anthony Tarkovsky's hash value was 12, we would only need to check the hashing table to see if 12 existed instead of searching through the name field for all 17 characters.

As you can't work out the original value from the hashed value, Hashing is also used to store passwords. Companies with poor security keep passwords in text fields, which can make it easier for passwords to be stolen. A more secure way to store passwords is the following: Much smarter companies do the following:

1. User enters password "thisisreallym3"
2. Database system hashes password to "fjj34N6*34£sdf234&" and stores this in the database.

Now when a customer returns to the site and enters their password the system does the following:

1. User enters password
2. Password entered is immediately hashed and the hashed value compared against the database value
3. If values are the same let them in, if values are different reject their log in attempt

This has the benefit of dealing with the following situation:

1. A script kiddie cracks into the system and steals the user database
2. They get user details with only the hashed value of the password
3. Hashed passwords are useless for finding out real passwords without the hashing algorithm (and mostly useless with it!)
4. Users' accounts on that website and other websites are not compromised even if they use the same password everywhere

Encryption

Hashing algorithms should do the following-

1. Have few collisions
2. Produce a wide range of hashed values
3. Produce the hashed output every time for the same input