Algebra/Chapter 2/Relations and Functions

2.12: Relations and Functions

---

Function as Box

Functions are another way of describing certain things mathematically. They are often described as a machine in a box open on two ends; you put something in one end, something happens to it in the middle, and something pops out the other end. The function is the machine inside, and it's defined by what it does to whatever you give it.

Let's say the machine has a blade that slices whatever you put into it in two and sends one half out the other end. If you put in a banana, you'd get back half a banana. If you put in an apple, you'd get back half an apple.

A good question to ask about this machine might be what happened to the other half of the piece of fruit? But, since this is algebra the things that go in and come out of functions will be numbers, so we're pretty sure the box won't fill up with numbers and break. Let's define the function to take what you give it and cut it in half, that is, divide it by two. If you put in 2, you'd get back 1. If you put in 57, you'd get back 28.5. The function machine allows us to alter expressions. Functions are typically named with a single letter. We'll call this one h for half. (There's nothing special about the letter we choose—we could just as well called this function f. The letter doesn't have to stand for anything.)

Now we need the notation. To put 2 into the function, we write $h(2)$ (read h of 2). We know that

$h(2)=1$

We can also calculate

$h(57)=28.5$

Using algebraic notation we can describe what this machine does as:

$h(x)={\frac {x}{2}}$

Instead of listing all the things we can put in our machine we represent them with a variable $x$. When we write $h(x)$ we are saying that we sent $x$ through the machine and it was cut in half. Using this form we don't have to count the halves that come out of our machine when we put 57 apples or oranges in our machine. We know that we put 57 or anything into our machine we will only have 28.5 of those things come out the other end. When using algebraic notation to specify a relationship; we have created something called an algebraic function definition. (This example illustrates the difference between mathematics and science and engineering. Since this is an imaginary machine we only need to specify what comes out the other end of the box. In real machines we also need to think about what to do with the halves that don't come out the other end).

Practice Problems

Use ^ on exponents

For problems 1-6, Use algebra to define the function described.

Example: x) Three-quarters of a number
 Answer: $f(x)=3x/4$

 

1 Four-fifths of a number

2 A number added to itself five times

3 A number increased by three times the number

4 A number multiplied by itself seven times, then reduced by the number

5 One number reduced by a different number three times

6 Half a number times three more than another number

Passing a number through the function box is called evaluating the function for a number. For problems 7-22, evaluate the described function for the given numbers.

Example: x) $f(x)=3x-4$
 a) $f(0)$ b) $f(4)$
 c) $f(1/3)$  d) $f(1/2)$
 
 Answer: a) $f(0)=3(0)-4=-4$   b) $f(4)=3(4)-4=8$
 c) $f(1/3)=3(1/3)-4=-3$ d) $f(1/2)=3(1/2)-4=-5/2$

 

$f(x)=10x$

7

$f(1)=$

8

$f(1/2)=$

9

$f(3.5)=$

10

$f(-1)=$

$g(x)=3x-1$

11

$g(4)=$

12

$g(2/3)=$

13

$g(1.1)=$

14

$g(-3)=$

$h(x)=x^{2}$

15

$h(7)=$

16

$h(3/5)=$

17

$h(5.3)=$

18

$h(-6)=$

$i(x)=1/(x-4)$

19

$i(5)=$

20

$i(2/3)=$

21

$i(7.25)=$

22

$i(0)=$

Function as Relation

Functions can also be thought of as a subset of relations. A relation is a connection between numbers in one set and numbers in another.

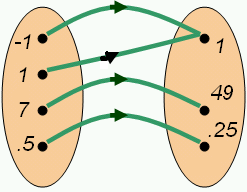
In other words, each number you put in is associated with each number you get out. The difference is that in a function, every 'input' number is associated with exactly one 'output' number whereas in a relation an 'input' number may be associated with multiple or no 'output' numbers. This is an important fact about functions. Notice that the relation depicted by the diagram above is not a function because it does not meet this requirement, unlike the relation depicted by the second diagram below, which is a function.

All functions are relations. Not all relations are functions.

Practice Problems

Which of the following definitions are functions and which are relations:

1 $f(x)=x+2$

	function
	relation

2 $g(x)=x-2$

	function
	relation

3 $h(x)=x*2$

	function
	relation

4 $i(x)=x/2$

	function
	relation

Which of the following definitions are functions and which are relations:

5 $j(x)=x+x$

	function
	relation

6 $k(x)=x-x$

	function
	relation

7 $l(x)=x*x$

	function
	relation

8 $m(x)=x/x$

	function
	relation

9 Can you write descriptions of the functions in problems 1-8: What is the difference? (answer on paper)

Domain and Range

Domain

The domain of a function is the set of 'input' numbers for which the function is defined. The domain is part of the definition of a function. In the function in the illustration above, the domain is {-1,1,7,1/2}.

The natural domain of an algebraically-defined function is the set of numbers for which the function is defined.

In most algebra formulas, x is usually the variable associated with Domain.

Example

The function $f(x)={\sqrt {x}}$ has a domain of $x\geq 0$ because the square root function is only defined for positive numbers (assuming that we are dealing with only real numbers).

Range

The range of a function is the set of results or solutions to the equation for a given input. A true function only has one result for every Domain.

In most algebra formulas, y is usually the variable associated with Range. As such, it can also be expressed f(x), which says that its value is a function of x.

Example

The function $f(x)=x^{2}$ has a range of $y\geq 0$ because the square of a number is always positive.

Functions in terms of Domain and Range

In taking both domain and range into account, a function is any mathematical formula that produces one and only one result for each input. Hence, it can be said that in a valid function, Domain (x) and Range (y) have a many to one correspondence so that every given Domain value has one and only one Range value as a result, but not necessarily vice versa. This makes sense since results can repeat, but inputs cannot.

As a result, if x is horizontal and y is vertical, a function in terms of y (e.g. y = mx + b) will produce a set of results such that if intersected by a vertical line at any point on the graph it will only pass through the graph once. An asymptotic function (one with at least one undefined result) would also count as valid since it did not pass through more than one point of the graph. This is called the "vertical line" test.

The terms domain and range can be applied to all relations and not just functions. A relation is a definition where one item in the definition's domain maps to more than one item in the definition's range. We use the terms domain and range to define the difference between a function and a relation.

A Bit of Function Terminology

When speaking or writing about functions, different terminologies are used to describe how the functions work or what they do.

f of x Terminology

When we write $f(x)$, we say f of x. Thus, if we have a function defined with the equation $g(x)={\frac {x+2}{7}}$ then we say that

g of x equals the sum of x and 2 altogether divided by 7.
or
g of x is x plus 2 all over 7.

When we plug a value (say 5) into the function for x we write $g(5)={\frac {5+2}{7}}={\frac {7}{7}}=1$ but we say that

g of 5 equals 1.

Algebraic notation is the easiest way mathematicians have to express relationships defined by arithmetic operators like $+,-./*,$ exponents, and roots. Once some of these functions have been defined it is easier to refer to the function name, and to refer to the values of the function as above.

Function "value of" Terminology

If we have a function defined with the equation $g(x)={\frac {x+2}{7}}$ then we say that The value of g at x is the sum of x and 2 altogether divided by 7. This way, $g(5)={\frac {5+2}{7}}={\frac {7}{7}}=1$