Biomechanics/The Biomechanics Of The Lung

Introduction

Cohesion

Binding interactions between molecules of the same type, mainly by H bonding.

Causes surface tension.

Adhesion

Binding interactions between molecules of different type, mainly by H bonding.

Causes lungs to be held to the inner side of the chest wall and diaphragm.

Surface tension = interface phenomenon that arises because cohesion of liquids is greater than adhesion of liquid to air: water molecules pull more towards each other than to air. Thus, water molecules are pulled down and sideways but not upwards. These uneven forces make the liquid surface rigid.
Surface tension for pure water is independent of the area. Unit = N / m.
With lungs we use compliance curves = ∆V / V0 versus F / A
The hysteresis between inspiration and expiration is due to E. loss caused when molecules rearrange themselves.
FRC = functional reserve capacity = V to which the chest is filled when no muscular work is done (3 liters).
Respiratory statics = study of the respiratory system when there is no convective flow of gas.
Plethysmograph = device used to measure lung volume.

Properties of isolated lung

In order to investigate lungs properties, we will compare 2 lungs: one filled with air (normal) and the other filled with a saline.

Remember that compliance = Strain / Stress = change in Volume / pressure

In air filled lungs

Have a lot of surface tension because there is an air-water interface in every alveolus.

Low compliance.

More P is required to expand the lung.

Large hysteresis.

In saline filled lungs

Have no surface tension.

High compliance.

Curve is steeper and switched to the left.

Small hysteresis. Thus, the main thing undergoing volume dependent re-arrangements has been removed.

Thus, lung tissue has a minor effect on elasticity (surface tension is the major effect).

• Elastic nature of lung tissue is due to elastin (stretchy) and collagen (stiff).

• At low lung V, both fibers are folded, so lung is very compliant.

• As lungs are expanded, more and more fibers are stretched beyond their resting lengths, making the lung more and more elastant.

• Changes in amount of collagen and elastin cause diseases: emphysema (too compliant), fibrosis (too elastant).

Lung washings experiment

 Lung washings are placed in a square-shaped trough with a dam that can be moved laterally to increase or decrease surface area of lung washings.

 A plate attached to a strain gauge is placed on the surface of the washings to record surface tension.

Results:

Surface tension of lungs washings is

 Lower than that of pure water.

 Area dependent.

Explanation:

 This is due to the presence of Lecithin surfactant.

 This surfactant has hydrophilic head and hydrophobic tail.

 The hydrophobic tail is fixed to alveolus wall.

 The hydrophilic head interacts with water, disrupting H bonds, which lowers the surface tension by decreasing the no. of water-water interactions.

 At low lung V, conc. of surfactant increases, so surface tension decreases.

 At high lung V, conc. of surfactant decreases, so surface tension increases.

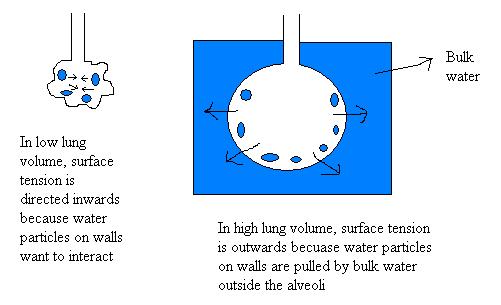
 The hysteresis between inspiration and expiration is because surface tension is always opposite to lung motion:

Inspiration

Surface tension is directed inwards because water molecules on the alveolus wall are trying to interact with each other.

Expiration

Surface tension is directed outwards because water molecules on the alveolus wall are pulled towards the bulk water outside the alveolus.

This opposite force creates an E. loss, shown as a hysteresis.

Effects of surfactant on breathing

1) Reduces work associated with breathing.

Work = ∫ P dV

Without surfactant: P is large so work is large.

With surfactant: P is small so work is small.

2) Reduces work needed to open nearly collapsed alveoli and avoid their collapse

Without surfactant: Work is large since surface tension is high.

With surfactant: Work is low since surface tension is lowered because surfactant disrupts H bonds.

3) Stabilizes alveolar size

Law of Laplace: P = 2T / r

Where P = pressure inside alveolus, T = surface tension, r = radius of alveolus.

For 2 connected alveoli, one small and the other large:

Without surfactant: P of small alveolus is large because r is small and T is constant.

As airflow goes from high P to low P, the small alveolus will empty into the larger one. Thus, - Total lung area decrease (area of large alveoli increases but they are few). - Less diffusion occurs.

With surfactant: P of small alveolus is nearly constant because, as r decreases, T decreases.

Thus, P is the same in small and large alveoli, and small alveoli do not empty into large ones.

Size of alveoli is thus stabilized.

Respiratory Distress Syndrome (RDS)

 It is associated with low-levels of surfactant.

 When a child is born prematurely (28th – 32nd week) lungs do not yet have surfactants. Thus, surfactant effects are absent and the child suffers from the previous problems.

 Disease can be detected during birth by determining the Sphingomyelin to Lecithin ratio of the amniotic fluid. If greater than 2 : 1, child has RDS.

 Note: sphingomyelin is always present in the amniotic fluid (constituent of plasma membranes) but high conc. of lecithin is associated with the secretion of surfactants.

Summary

• Compliance of the lungs is due to both surface tension and elastic properties of lungs.

• In normal lungs, most stiffness is due to surface tension (although it is greatly reduced as area decreases, due to surfactants).

• Surfactants decrease surface tension and thus decrease E. loss and hysteresis.

• Change in tissue compliance or in surfactants causes diseases.

Mechanics of respiration

 IPP = intra-pleural pressure, the dynamics of lung mechanism. It is always lower than the atmosphere (-ve relative to atm). This is to allow lungs to expand: if it was equal or greater than atm, lungs wouldn’t expand and inspiration wouldn’t occur.

 Example: if Patm = 5 and IPP = 2, IPP is 3 –ve relative to atm. If IPP reduces 1, then IPP is 4 –ve relative to atm, thus more –ve. But if IPP = 6, no inspiration (unless we take a forced breath).

Inspiration

Diaphragm contracts and enlarges pleural cavity, which reduces IPP.

As IPP reduces (becomes more –ve), it makes suction of lung walls outwards.

As V of lungs ↑, Palv ↓.

As airflow goes from high P to low P, air enters the lungs.

Since –ve Palv is needed to inspire air, air current is –ve.

Conclusion: IPP, Palv and airflow become more –ve, V becomes more +ve.

Expiration

Diaphragm relaxes and reduces pleural cavity, which increases IPP.

As IPP increases (becomes less –ve), it releases lungs and recoil forces push lung walls inwards.

As V of lungs ↓, Palv ↑

As airflow goes from high P to low P, air exits the lungs.

Since +ve Palv is needed to expire air, air current is +ve.

Conclusion: IPP, Palv and airflow become more +ve (with IPP still –ve), V more –ve.

Notes:

- Surface tension was thus always opposite to IPP during inspiration and to recoil force during expiration.

- IPP is also –ve relative to Palv because alveoli are connected to atm by open tubes.

- In the curve, Palv begins with 0 (same P as atm), but IPP begins –ve.

- If IPP > atm, air current is always +ve (out of lungs) unless we take a forced breath to make maximum contraction, making IPP –ve, and allowing air to enter.

- If density and height are given, ∆P is calculated by: ∆P = ρ g h.

Analogy with Electricity

1) Ohm’s Law

a) Current

I = ∆v / R

I = q / t

I = Electric current (A)

∆v = Potential difference (V)

R = Electric resistance (Ω)

q / t = no. of charge flowing per unit time

b) Resistance

R = ∆v / I

R = (ρ L) / (π r2)

ρ = Resistivity (Ω.m)

L = Length of resistor (cm)

π r 2　　= Area of resistor (cm2)

c) Work done

W = V I t (joule)

d) Power

Power = V I (watt)

e) Series resistance

As current flows in various resistances,

I1 = I2

f) Parallel resistances

As current divides in different resistances,

1/ Rt = 1/R1 + 1/R2 + … + 1/R3

g) Capacitance

C = q / v

High capacitance = conserve a high no. of charges (q) for a low voltage (v).

2) Poiseuille’s Law

a) Current

Q = ∆P / R

Q = V / t

Q = Fluid current (mL/sec)

∆P = Pressure diff. (cm H2O)

R = Flow resistance (poise / cm3　　)

V / t = Volume of particles flowing per unit time.

b) Resistance

R = ∆P / Q

R = (8 η L) / (π r 4)

η = Viscosity coeff. of fluid (poise)

L = Length of tube. (cm)

π r 4　　= (cm4)

c) Work done

W = P Q t = P (V / t) t ----> W = P V (joule)

d) Power

Power = P Q = P (V / t)

Power = P V / t (watt)

e) Series resistance

As air flows in respiratory tree, from trachea to bronchi to alveoli,

Q1 = Q2 ----> V1 / t = V2 / t ----> (A1 L1) / t = (A2 L2) / t ----> A1 v1 = A2 v2

This is the continuity eqn. Air thus flows quickly in small areas and slowly in large areas.

f) Parallel resistances

As each bronchus divides into 2 of smaller sizes, and each divides into 2 and so on, forming generations: 1/ Rt = 1/R1 + 1/R2 + … + 1/R3

Note: in most generations of bronchi, the airway R decreases slightly. To do so, each bronchus has to divide into 2 bronchi with r2 > 0.84 r1. (if r2 = 0.84 r1, R is const.)

g) Capacitance

C = V / P

This is actually the compliance.

High compliance = great strain (V) for low stress (P).

E.g. C of lungs = 200 mL/ cm H2O.

If it is 50, when IPP makes suction of the wall, it doesn’t stretch enough and there is a problem in respiration.

Note:

The last table is valid for the flow of air in lungs and flow of blood in arteries.

Previous: The Biomechanics Of Skeletal Muscles part 2
Next: Hemodynamics