Calculus/Precalculus/Solutions

Convert to interval notation

1. $\{x:-4<x<2\}\,$

$\mathbf {(-4,2)}$

2. $\{x:-{\frac {7}{3}}\leq x\leq -{\frac {1}{3}}\}$

$\mathbf {[-{\frac {7}{3}},-{\frac {1}{3}}]}$

3. $\{x:-\pi \leq x<\pi \}$

$\mathbf {[-\pi ,\pi )}$

4. $\{x:x\leq 17/9\}$

$\mathbf {(-\infty ,{\frac {17}{9}}]}$

5. $\{x:5\leq x+1\leq 6\}$

$4\leq x\leq 5$
$\mathbf {[4,5]}$

6. $\{x:x-1/4<1\}\,$

$x<1{\frac {1}{4}}={\frac {5}{4}}$
$\mathbf {(-\infty ,{\frac {5}{4}})}$

7. $\{x:3>3x\}\,$

$1>x$

$x<1$

$\mathbf {(-\infty ,1)}$

8. $\{x:0\leq 2x+1<3\}$

$-1\leq 2x\leq 2$

$-{\frac {1}{2}}\leq x<1$

$\mathbf {[-{\frac {1}{2}},1)}$

9. $\{x:5<x{\mbox{ and }}x<6\}\,$

This is equivalent to $5<x<6$
$\mathbf {(5,6)}$

10. $\{x:5<x{\mbox{ or }}x<6\}\,$

It helps to draw a picture to determine the set of numbers described:

A number in the set can be on either the red or blue line, so the entire number line is included.

$\mathbf {(-\infty ,\infty )}$

State the following intervals using set notation

11. $[3,4]\,$

$\mathbf {\{x:3\leq x\leq 4\}}$

12. $[3,4)\,$

$\mathbf {\{x:3\leq x<4\}}$

13. $(3,\infty )$

$\mathbf {\{x:x>3\}}$

14. $(-{\frac {1}{3}},{\frac {1}{3}})\,$

$\mathbf {\{x:-{\frac {1}{3}}<x<{\frac {1}{3}}\}}$

15. $(-\pi ,{\frac {15}{16}})\,$

$\mathbf {\{x:-\pi <x<{\frac {15}{16}}\}}$

16. $(-\infty ,\infty )$

$\mathbf {\{x:x\in \Re \}}$

Which one of the following is a true statement?

17. $|x+y|=|x|+|y|\,$

Let $x=-5,y=5$. Then

$|x+y|=|-5+5|=|0|=0$, and
$|x|+|y|=|-5|+|5|=5+5=10$
Thus, $|x+y|\neq |x|+|y|$

false

18. $|x+y|\geq |x|+|y|$

Using the same example as above, we have $|x+y|\ngeq |x|+|y|$.
false

19. $|x+y|\leq |x|+|y|$

true

Evaluate the following expressions

20. $8^{1/3}\,$

$(2^{3})^{1/3}=2^{1}=\mathbf {2}$

21. $(-8)^{1/3}\,$

$(-2^{3})^{1/3}=-2^{1}=\mathbf {-2}$

22. ${\bigg (}{\frac {1}{8}}{\bigg )}^{1/3}\,$

$({\frac {1}{2^{3}}})^{1/3}=(2^{-3})^{1/3}=2^{-1}=\mathbf {\frac {1}{2}}$

23. $(8^{2/3})(8^{3/2})(8^{0})\,$

$8^{{\frac {2}{3}}+{\frac {3}{2}}+0}=8^{{\frac {4}{6}}+{\frac {9}{6}}}=8^{\frac {13}{6}}=(2^{3})^{\frac {13}{6}}=\mathbf {2^{13/2}}$

24. ${\bigg (}{\bigg (}{\frac {1}{8}}{\bigg )}^{1/3}{\bigg )}^{7}$

$(({\frac {1}{2^{3}}})^{1/3})^{7}=((2^{-3})^{1/3})^{7}=(2^{-1})^{7}=2^{-7}={\frac {1}{2^{7}}}=\mathbf {\frac {1}{128}}$

25. ${\sqrt[{3}]{\frac {27}{8}}}$

$({\frac {27}{8}})^{1/3}=({\frac {3^{3}}{2^{3}}})^{1/3}={\frac {3^{1}}{2^{1}}}=\mathbf {\frac {3}{2}}$

26. ${\frac {4^{5}\cdot 4^{-2}}{4^{3}}}$

$4^{5-2-3}=4^{0}=\mathbf {1}$

27. ${\bigg (}{\sqrt {27}}{\bigg )}^{2/3}$

$((3^{3})^{1/2})^{2/3}=(3^{\frac {3}{2}})^{\frac {2}{3}}=3^{1}=\mathbf {3}$

28. ${\frac {\sqrt {27}}{\sqrt[{3}]{9}}}$

${\frac {(3^{3})^{1/2}}{(3^{2})^{1/3}}}={\frac {3^{\frac {3}{2}}}{3^{\frac {2}{3}}}}=3^{{\frac {3}{2}}-{\frac {2}{3}}}=3^{{\frac {9}{6}}-{\frac {4}{6}}}=\mathbf {3^{5/6}}$

Simplify the following

29. $x^{3}+3x^{3}\,$

$\mathbf {4x^{3}}$

30. ${\frac {x^{3}+3x^{3}}{x^{2}}}$

$\mathbf {4x}$

31. $(x^{3}+3x^{3})^{3}\,$

$\mathbf {64x^{9}}$

32. ${\frac {x^{15}+x^{3}}{x}}$

$\mathbf {x^{14}+x^{2}}$

33. $(2x^{2})(3x^{-2})\,$

$\mathbf {6}$

34. ${\frac {x^{2}y^{-3}}{x^{3}y^{2}}}$

$\mathbf {\frac {1}{xy^{5}}}$

35. ${\sqrt {x^{2}y^{4}}}$

$\mathbf {xy^{2}}$

36. ${\bigg (}{\frac {8x^{6}}{y^{4}}}{\bigg )}^{1/3}$

$\mathbf {\frac {2x^{2}}{y^{\frac {4}{3}}}}$

Find the roots of the following polynomials

37. $x^{2}-1\,$

$x=\pm 1$

38. $x^{2}+2x+1\,$

$x=-1$

39. $x^{2}+7x+12\,$

$x=-3,x=-4$

40. $3x^{2}-5x-2\,$

$x=2,x=-{\frac {1}{3}}$

41. $x^{2}+5/6x+1/6\,$

$x=-{\frac {1}{3}},x=-{\frac {1}{2}}$

42. $4x^{3}+4x^{2}+x\,$

$x=0,x=-{\frac {1}{2}}$

43. $x^{4}-1\,$

$x=\pm i,x=\pm 1$

44. $x^{3}+2x^{2}-4x-8\,$

$x=\pm 2$

Factor the following expressions

45. $4a^{2}-ab-3b^{2}\,$

$(4a+3b)(a-b)$

46. $(c+d)^{2}-4\,$

$(c+d+2)(c+d-2)$

47. $4x^{2}-9y^{2}\,$

$(2x+3y)(2x-3y)$

Simplify the following

48. ${\frac {x^{2}-1}{x+1}}\,$

$x-1,x\neq -1$

49. ${\frac {3x^{2}+4x+1}{x+1}}\,$

$3x+1,x\neq -1$

50. ${\frac {4x^{2}-9}{4x^{2}+12x+9}}\,$

${\frac {2x-3}{2x+3}}$

51. ${\frac {x^{2}+y^{2}+2xy}{x(x+y)}}\,$

${\frac {x+y}{x}},x\neq -y$

Functions

52. Let $f(x)=x^{2}$.

a. Compute $f(0)$ and $f(2)$.

$f(0)=0$, $f(2)=4$

b. What are the domain and range of $f$?

The domain is $(-\infty ,\infty )$; the range is $[0,\infty )$,

c. Does $f$ have an inverse? If so, find a formula for it.

No, since $f$ isn't one-to-one; for example, $f(-1)=f(1)=1$.

53. Let $f(x)=x+2$, $g(x)=1/x$.

a. Give formulae for

i. $f+g$

$(f+g)(x)=x+2+1/x=(x^{2}+2x+1)/x$.

ii. $f-g$

$(f-g)(x)=x+2-1/x=(x^{2}+2x-1)/x$.

iii. $g-f$

$(g-f)(x)=1/x-x-2=(1-x^{2}-2x)/x$.

iv. $f\times g$

$(f\times g)(x)=(x+2)/x$.

v. $f/g$

$(f/g)(x)=x(x+2)$ provided $x\neq 0$. Note that 0 is not in the domain of $f/g$, since it's not in the domain of $g$, and you can't divide by something that doesn't exist!

vi. $g/f$

$(g/f)(x)=1/[x(x+2)]$. Although 0 is still not in the domain, we don't need to state it now, since 0 isn't in the domain of the expression $1/[x(x+2)]$ either.

vii. $f\circ g$

$(f\circ g)(x)=1/x+2=(2x+1)/x$.

viii. $g\circ f$

$(g\circ f)(x)=1/(x+2)$.

b. Compute $f(g(2))$ and $g(f(2))$.

$f(g(2))=5/2$; $g(f(2))=1/4$.

c. Do $f$ and $g$ have inverses? If so, find formulae for them.

Yes; $f^{-1}(x)=x-2$ and $g^{-1}(x)=1/x$. Note that $g$ and its inverse are the same.

54. Does this graph represent a function?

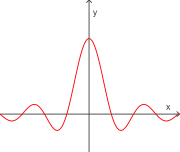
As pictured, by the Vertical Line test, this graph represents a function.

55. Consider the following function

$f(x)={\begin{cases}-{\frac {1}{9}}&{\mbox{if }}x<-1\\2&{\mbox{if }}-1\leq x\leq 0\\x+3&{\mbox{if }}x>0.\end{cases}}$

a. What is the domain?

${(-\infty ,\infty )}$

b. What is the range?

${(-1/9,\infty )}$

c. Where is $f$ continuous?

${x>0}$

56. Consider the following function

$f(x)={\begin{cases}x^{2}&{\mbox{if }}x>0\\-1&{\mbox{if }}x\leq 0.\end{cases}}$

a. What is the domain?

${(-\infty ,\infty )}$

b. What is the range?

${(-1,\infty )}$

c. Where is $f$ continuous?

${x>0}$

57. Consider the following function

$f(x)={\frac {\sqrt {2x-3}}{x-10}}$

a. What is the domain?

${(3/2,10)\cup (10,\infty )}$

b. What is the range?

${(-\infty ,\infty )}$

c. Where is $f$ continuous?

${(3/2,10)and(x>10)}$

58. Consider the following function

$f(x)={\frac {x-7}{x^{2}-49}}$

a. What is the domain?

${(-\infty ,-7)\cup (-7,\infty )}$

b. What is the range?

${(-\infty ,\infty )}$

c. Where is $f$ continuous?

${(-\infty ,-7)and(-7,\infty )}$

Graphing

59. Find the equation of the line that passes through the point (1,-1) and has slope 3.

$3x-y=4$

60. Find the equation of the line that passes through the origin and the point (2,3).

$3x-2y=0$