Cellular Automata/Listing Preimages

Two algorithms are described for listing the preimages of a present configuration. The first algorithm is described in many texts by Andrew Wuensche the second is introduced in this book.

Preimage network

A new graph the preimage network is introduced to facilitate the description of reverse algorithms in terms of paths through the graph.

The preimage diagram of a single cell is the network of preimages of that cell. Like preimage matrices of cells in a sequence $\alpha =c_{0},c_{1},\dots ,c_{x},\dots ,c_{l-1}$ length $l$ are aligned into a chain and multiplied, preimage diagrams for each of the cells can be aligned to form the preimage network. If all the links in the De Bruijn diagram are taken into account, than only those representing neighborhoods that are mapped into the observed cell are valid links. Each link or path consisting of many links between nodes in the diagram is a locally valid path.

Elements $d_{o_{L}o_{R}}$ in the multiplied preimage matrix $D(\alpha )$ count the preimages beginning at one of the left overlaps $o_{L}=o_{0}$ and ending at one of the right overlaps $o_{L}=o_{l}$ . In the same way there are $d_{o_{L}o_{R}}$ different valid paths between the two overlaps in the preimage network.

The definition of what is globally valid depends on whether the finite lattice is bounded or cyclic.

On a bounded lattice a globally valid path connects any overlap on the left boundary to any overlap at the right boundary.
on a cyclic lattice a globally valid path must begin and end at the same overlap value.

A node on a locally valid path is a locally valid node. A node on a globally valid path is a globally valid node.

The arrows that point the links in the increasing direction of the position index can be omitted.

Link weights

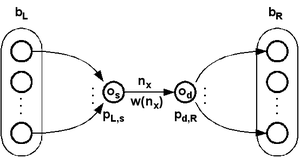
Overlaps and neighborhoods in the preimage network can be weighted depending on the number of globally valid paths passing through them. The weights can be illustrated on the preimage network as node size (not used in the examples) and line thickness. Since the number of preimages may increase exponentially the thickness may be a logarithm of the weight.

w_{log}=\log _{|S|}w

There are two different ways to define and calculate weights depending on whether the finite lattice is bounded or cyclic.

Bounded lattice

The weights for links $n_{x}=o_{s}c_{s}=c_{d}o_{d}$ at position index $x$ are the product of:

the number of paths $p_{b_{L},o_{s}}$ from left boundary $b_{L}$ to the source overlap $o_{s}$ and
the number of paths $p_{o_{d},b_{R}}$ from the drain overlap $o_{d}$ to the right boundary $b_{R}$ .

w(n_{x})=p_{b_{L},0_{s}}\cdot p_{o_{d},b_{R}}

Both parts of the product are contained inside preimage vectors, $b_{s}$ for the left part and $b_{d}$ for the right part.

b_{s}=b_{L,x}=b_{L}D(c_{0}c_{1}\dots c_{x-1})

b_{d}=b_{x+1,R}=D(c_{x+1}c_{x+2}\dots c_{l-1})b_{R}

Cyclic lattice

On a cyclic lattice the weights for links $n_{x}=o_{s}c_{s}=c_{d}o_{d}$ at position index $x$ are the sum over overlaps of products of:

the number of paths $p_{o_{L},o_{s}}$ from one left overlap $o_{L}$ to the source overlap $o_{s}$ and
the number of paths $p_{o_{d},o_{R}}$ from the drain overlap $o_{d}$ to the right boundary $b_{R}$ .

w(n_{x})=\sum _{o=0}^{|S|^{k-1}-1}p_{o,o_{s}}\cdot p_{o_{d},o}

Because boundary overlaps must be distinguished the preimage vector is not enough and the information on the number of paths is contained in preimage matrices.

D_{L,x-1}(c_{0}c_{1}\dots c_{x-1})\qquad D_{x+1,R}(c_{x+1}c_{x+2}\dots c_{l-1})

Computing weights

To compute all the link weights both preimage counts from the left boundary to each cell and from the right boundary to each cell are needed. For bounded lattices the counts are stored in preimage vectors, for cyclic lattices counts are stored in preimage matrices.

Bounded lattice

For bounded lattices the preimage counts are stored as preimage vectors. The first counts at the left $b_{L,0}$ and the right $b_{l,R}$ are boundary vectors.

b_{L,0}=b_{L}\qquad b_{l,R}=b_{R}^{T}

Left sided counts $b_{L,x}$ are calculated from the left to the right, the vector at position $x$ is calculated from the vector at position $x-1$ . Right sided counts $b_{x,R}$ are calculated from the right to the left, the vector at position $x$ is calculated from the vector at position $x+1$ .

b_{L,x}=D(c_{0}c_{1}\dots c_{x-1})b_{R}^{T}=b_{L,x-1}D(c_{x-1})

b_{x,R}=D(c_{x}c_{x+1}\dots c_{l-1})b_{R}^{T}=D(c_{x})b_{x+1}

The total number of all preimages is calculated by applying both boundaries.

p=b_{L}D(\alpha )b_{R}^{T}=b_{L}b_{0,R}=b_{L,l}b_{R}^{T}

Algorithm pseudo-code for counting from the left to the right

b[0] = b_L                     # the left preimage vector b[0] is initialized to the left boundary b_L
for ( x=1; x<=l; x++ )         # run the position index from the left (x=0) to the right (x=l-1)
  b[x] = b[x-1]*D[C[x-1]]      # the new preimage vector is calculated from the old using the
end                            # preimage matrix D[C[x-1]] of the cell value C[x-1] at position x-1

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += b[l][o] * b_R[o]        # the last right preimage vector b[l] and the right boundary vector b_R
end                            #

Algorithm pseudo-code for counting from the right to the left

b[l] = b_R                     # the right preimage vector b[l] is initialized to the right boundary b_R
for ( x=l-1; x>=0; x-- )       # run the position index from the right (x=l-1) to the left (x=0)
  b[x] = D[C[x]]*b[x+1]        # the new preimage vector is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += b_L[o] * b[0][o]        # the last left preimage vector b[0] and the left boundary vector b_L
end                            #

Example:

Preimage graphs for two sequences in rule 110

Cyclic lattice

For cyclic lattices the counts are stored as preimage matrices, this is necessary to distinguish counts for each of the overlaps at the joined boundaries. Since the lattice is cyclic, there is no need to apply a boundary vector as in the bounded lattice.

Left sided counts $D_{L,x}$ are calculated from the left to the right, the matrix at position $x$ is calculated from the matrix at position $x-1$ . Right sided counts $D_{x,R}$ are calculated from the right to the left, the matrix at position $x$ is calculated from the matrix at position $x+1$ .

D_{L,x}=D(c_{0}c_{1}\dots c_{x-1})=D_{L,x-1}D(c_{x-1})

D_{x,R}=D(c_{x}c_{x+1}\dots c_{l-1})=D(c_{x})D_{x+1,R}

The number of preimages must be counted separately for each of the $|S|^{k-1}$ overlaps at the joined boundaries $o_{L}=o_{0}=o_{l}=o_{R}$ . A cyclic preimage (row) vector $b_{\circ }(\alpha )$ is constructed from the diagonal elements of the preimage matrix $D(\alpha )$ .

D(\alpha )=D_{0,R}=D_{L,l-1}

b_{\circ }(\alpha )=\left[d_{0,0}(\alpha ),d_{1,1}(\alpha ),\dots ,d_{|S|^{k-1},|S|^{k-1}}(\alpha )\right]

The total number of all preimages is the sum of the elements in the cyclic preimage vector $b_{\circ }(\alpha )$ (row), the scalar product with the unrestricted boundary vector $b_{u}$ (row transposed into column).

p=b_{\circ }(\alpha )b_{u}^{T}

Algorithm pseudo-code for counting from the left to the right

D[0] = I                       # the left preimage matrix D[0] is initialized to the identity matrix
for ( x=1; x<l; x++ )          # run the position index from the left (x=0) to the right (x=l-1)
  D[x] = b[x-1]*D[C[x]]        # the new preimage matrix is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += D[l-1][o][o]              # the sum of the diagonal elements of the right preimage matrix D(l-1)
  b_0[o] = D[0][o][o]          # the diagonal are copied into the cyclic preimage vector b_0
end                            #

Algorithm pseudo-code for counting from the right to the left

D[l] = I                       # the right preimage matrix D[l] is initialized to the identity matrix
for ( x=l-1; x>=0; x-- )       # run the position index from the right (x=l-1) to the left (x=0)
  D[x] = D[C[x]]*b[x+1]        # the new preimage matrix is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += D[0][o][o]              # the sum of the diagonal elements of the left preimage matrix D(0)
  b_0[o] = D[0][o][o]          # the diagonal are copied into the cyclic preimage vector b_0
end                            #

Example:

Preimage graphs for two sequences in rule 110

String operations

Preimages as paths in the preimage network are described in terms of neighborhoods and overlaps, which are both sequences of cells. Since neighborhoods on a globally valid path overlap, each cell can be found in $k$ neighborhoods and in $k$ overlaps.

Neighborhoods are represented by links in the preimage diagrams and networks. The neighborhood $n_{x}$ surrounding the cell $c_{x}$ is defined as

n_{x}=c_{x-k_{0}}c_{x-k_{0}+1}\dots c_{x}\dots c_{x+k-k_{0}-1}

Overlaps are represented by nodes in the preimage diagrams and networks. The overlap $o_{x}$ surrounding the cell $c_{x}$ is defined as

o_{x}=c_{x+1-k_{0}}c_{x+2-k_{0}}\dots c_{x}\dots c_{x+k-k_{0}-1}

Sequences can be represented and manipulated in two ways:

compact representations are manipulated using algebraic operations (multiplication, division (quotient without remainder) and modulo)
bit arrays are manipulated using boolean logical operations (shifts, fusion with OR and masking with AND) each cell consumes $m=top(\log _{2}|S|)$

Extracting the observed cell

Extracting from the neighborhood

Algebraic notation

c_{x}=n_{x}/|S|^{k-k_{0}-1}\mod |S|

Logic notation

c_x = (n_x >> m*(k-k_0-1)) AND (2^m-1)

Extracting from the overlap

Algebraic notation

c_{x}=o_{x}/|S|^{k-k_{0}}\mod |S|

Logic notation

c_x = (o_x >> m*(k-k_0)) AND (2^m-1)

Transformations between overlaps and neighborhoods

Extending an overlap into a neighborhood

A neighborhood $n$ (length $k$ ) is created from an overlap $o$ (length $k-1$ ) by adding one cell $c$ at the left or the right side.

String notation (concatenation of cell strings)

n_{x}=o_{x}c_{x+k-k_{0}-1}

n_{x-1}=c_{x-k_{0}-1}o_{x}

Algebraic notation

n_{x}=o_{x}\cdot |S|+c_{x+k-k_{0}-1}

n_{x-1}=c_{x-k_{0}-1}\cdot |S|^{k-1}+o_{x}

Logic notation

n_x = (o_x << m) OR c

n_x-1 = (c << m(k-1)) OR o_x

Shortening a neighborhood into an overlap

An overlap $o$ (length $k-1$ ) is created from a neighborhood $n$ (length $k$ ) by removing one cell $c$ at the left or the right side.

String notation

$\alpha \,/\,a$ means string $\alpha$ without the extreme right symbol $a$
$b\setminus \beta$ means string $\beta$ without the extreme left symbol $b$ )

o_{x}=n_{x}\,/\,c_{x+k-k_{0}-1}\quad \Rightarrow \quad n_{x}=o_{x}c_{x+k-k_{0}-1}

o_{x+1}=c_{x-k_{0}}\setminus n_{x}\quad \Rightarrow \quad n_{x}=c_{x-k_{0}}o_{x+1}

Algebraic notation

o_{x}=n_{x}/|S|

o_{x+1}=n_{x}mod|S|^{k-1}

Logic notation

n_x = o_x >> m

n_x+1 = o_x AND (2^(m*(k-1))-1)

Trace and backtrack algorithm

This algorithm traces paths through the preimage diagram. It starts at the first node at the left that is not masked by left boundary conditions. Depending on the position index value and whether there are links to the right there are four options:

tracing the first unused valid link to the next node and remembering the selected path
if the reached node is at the right boundary, validity of the boundary is tested and the path is stored as a preimage
if there are no unused links to the right, backtrack to the previous node on the current path
when backtracking reaches the left boundary, the tracing restarts at the next valid node till all nodes are exhausted.

The algorithm could start at the right and trace to the left obtaining the same preimages. The direction tracking is chosen so that the listed preimages are sorted in an ascending order regarding their compact representation.

Fromal algorithm description

Most parts of the algorithm are identical for bounded and cyclic latices, the differences are seen only at the boundaries.

Main loop and left boundary

The main loop counts through the available tracing start points. The algorithm begins tracing by the first overlap at the left $o=o_{L}=0$ (on bounded lattices overlaps masked by the left boundary $b_{L}$ are skipped). When all the traces beginning with this overlap are exhausted (backtracking reaches the left boundary $x=0$ and the link index exceeds the number of available links $c=|S|$ ) tracing continues to the next valid overlap $o_{L}=o_{L}+1$ till it reaches the last overlap $o_{L}=|S|^{k-1}-1$ . When traces from the last overlap are exhausted the algorithm finishes. On bounded lattices overlaps may be unrestricted or masked by a boundary vector $b_{L}$ . On cyclic latices all overlaps are used.

Tracing

The tracing increments the current position index $x=x+1$ . Each tracing step begins at the current overlap $o_{x}$ at position $x$ and traces the first not yet traced link to the drain overlap $o_{d}$ at position index $x+1$ . There are $|S|$ links to be traced, if the current overlap has not yet been backtracked than tracing begins at link $c=0$ otherwise the link provided by the backtracking is incremented. The validity of the trace step must be verified, each link represents a neighborhood $n=o_{s}c$ that must lead to the present cell value $f(n_{x}^{t-1})=c_{x}^{t}$ .

If the link is valid, its index $c$ is stored as a new cell $c_{x+k-k_{0}-1}=c$ on the currently traced path and the algorithm continues from the drain node $o_{d}=c_{x-k_{0}}\setminus o_{x}c_{x+k-k_{0}-1}$ .
If the link is not valid than the tracing must proceed with the next link $c=c+1$ , if there are no links left $c=|S|$ than the algorithm switches to backtracking.

Backtracking

Backtracking is returning back on the current path till the point where an available link for tracing is found. The current overlap without further paths is $o_{x}$ each backtracking step steps backward on the current path over the link $n_{x-1}$ to the overlap $o_{s}$ at position index $x-1$ . The backward link $n_{x-1}=c_{x-k_{0}-1}o_{x}$ and the source overlap $n_{x-1}=c_{x-k_{0}-1}o_{x}\;/\;c_{x+k-k_{0}-2}$ are sequences on the current path. When back at the source cell, the link to trace forward is incremented from the last traced link $c=c_{x+k-k_{0}-2}+1$ .

Right boundary and listing of preimages

When tracing reaches the right boundary listing a preimage can begin.

For cyclic lattices the current overlap $o_{x}$ is compared to the starting overlap at the left $o_{L}$ , if they are equal a preimage $C^{t-1}=c_{0}c_{1}\dots c_{l-1}$ of length $l$ is added to the preimage list.
For bounded lattices the current overlap $o_{x}$ is masked by the right boundary vector $b_{R}$ , if accepted a preimage $C^{t-1}=c_{-k_{0}}\dots c_{l+k-k_{0}-1}$ of length $l+k-1$ is added to the preimage list.

For each new preimage the preimage counter $p$ is incremented.

Algorithm pseudo-code

p=0                               # the preimage counter is initialized to 0
x=0                               # the position index is initialized to 0
c=0                               # the link index is initialized to 0
o_L=0                             # the tracing starts at the first left overlap
while (bounded) then              # if the lattice is bounded
  if ( b[o_L]>0 ) then            # boundary conditions must be checked
    o_L++                         # to ensure the start point is valid
  end_if                          #
end_while                         #
o=o_L                             # the current overlap is initialized

while (o_L<|S|^(k-1)) then        ## main loop ##

if ( c<|S| ) then                 # tracing and right boundary

  if ( x<l ) then                 ## tracing ##
    n=o*|S|+c                     # the neighborhood is created
    if ( f(n)==c_x ) then         # checking it the neighborhood is valid
      o=(o*|S|+c)/|S|^k           # stepping to the new overlap at the right
      C[x+k-k0-1]=c               # storing the link selection cell
      x++                         # incrementing the position index
      c=0                         # at the new overlap start with the first link
    else                          # the selected link is not valid
      c++                         # try the next link
    end_if                        #
  end_if                          #

  else                            ## right and cyclic boundary conditions ##
    if (bounded)                  # for bounded lattices
      if ( b[o]>0 ) then          # check masking of the current overlap with the right boundary vector
        store(C)                  # list the preimage consisting of cells on the current path
      end_if                      #
    end_if                        #
    if (cyclic)                   # for cyclic lattices
      if ( o==o_L ) then          # check if overlaps at the left and right boundary are equal
        store(C)                  # list the preimage consisting of cells on the current path
      end_if                      #
    end_if                        #
    c=|S|                         # to prevent further tracing from the boundary
  end_if                          #
 
else                              # backtracking and left boundary

  if ( x==0 ) then                ## left boundary conditions ##
    o_L++                         # move to the next start point for tracing
    if (bounded) then             # for bounded lattices
      if ( b[o_L]>0 )             # check masking of the left overlap by the left boundary vector
        c=0                       # move to the next start point for tracing
      else                        # else if the current overlap is not valid
        o_L++                     # move to the next start point for tracing
      end_if                      #
    else_if (cyclic) then         # for cyclic lattices
      c=0                         #
    end_if                        #

  else                            ## backtracking ##
    o=(C[x-k0-1]*|S|^(k-1)+o)/|S| # backtracking to the previous overlap
    c=C[x+k-k0-1]                 # restoring the last used link at this overlap
    c++                           # at the backtracked overlap continue with the next link
    x--                           # decrementing the position index
  end_if                          #

end_if

end                               # if all start points are exhausted end the algorithm

Algorithm complexity

The algorithm can be divided into two time consuming operations

tracing and backtracking
listing preimages

The algorithm visits all links and nodes accessible from the boundary where it starts. Accessibilyti of overlaps and neighborhoods is defined as an induction:

Base: Overlaps $o$ at the starting boundary $b_{L}$ (left here) are acessible if they are valid $b_{L}(o)>0$ .
Induction: Every neighborhood sourced at an acessible node is acessible. Every drain overlap to an acessible and valid neighborhood is acessible.

The valid accessible links are visited exactly twice (first while tracing and secondly while backtracking), invalid lins are visited only once (their validity is evaluated by tracing). A simple aproximation for the tracing time is counting all the accessible overlaps, counting must be performed for each of the overlaps at the boundary so preimage matrices must be used for counting.

An arbitrary overlap $o_{x}$ is accessible from a valid overlap $o_{L}$ at the left boundary if there is at least one valid path between the two $p_{o_{L},o_{x}}>0$ . Accessibility of overlaps at position index $x$ can be extracted from the preimage matrix $D_{L,x}$ by transformning its elements into boolean values or by using bolean multiplication to calculate preimage matrices $D^{B}$ . The algorithm complexity of tracing is the sum of all accessible overlaps.

T_{trace}=\sum _{x=0}^{l-1}b_{L}D_{L,x}^{B}b_{u}^{T}

The upper boud to the processing time is a linear function of the observed configuration size $l$ but grows exponentially with the increasing neighborhood size (preimage diagram size).

T_{trace}=O(l\cdot |S|^{2(k-1)})

The time required for listing of preimages $T_{list}$ is a linear function of the number of preimages $p$ , where the time to compute a single preimage is a linear function of the configuration length $l$ .

T_{list}=C_{list}lp=O(lp)\,

Memory consumption of the algorithm is minimal, only the current path in the preimage network is stored and used for listing if a valid preimage is found.

Count and list algorithm

This algorithm consists of a first backward or counting pass that counts the preimages and a second forward or listing pass that lists them. The trace and backtrack algorithm must trace each link before knowing if it leads to a valid preimage, on the other hand the counting pass produces information obout wheather and how many preimages there are for each link. All the preimages can be listed without backtracking.

The direction of the listing pass could be inverted but is chosen so that the listed preimages are sorted in an ascending order regarding their compact representation, the counting pass is in the opposite direction.

Formal algorithm description

Booth the forward (left to right, producing $b_{L,x}$ vectors) and backward (right to left, producing $b_{x,R}$ vectors) counting passes have been described above, while computing weights for the preimage network. Only one of the passes is needed, here the backward pass is used.

The listing pass can be divided into initialization and a few steps inside the main loop.

Initialization

Since the number of preimages $p$ has been calculated by the counting pass, memory can be allocated for them in advance. The array of starting overlaps $o_{L}$ holds the value of the starting point for each preimage (valid path in the preimage network). The number of preimages using each starting overlap is computed as a weight vector for overlaps at the left boundary. For bounded lattices the left boundary and the preimage count from the righ end to the left are used.

w_{0}(o)=b_{L}(o)b_{0,R}(o)\,

For cyclyc lattices the preimage matrix of the whole sequence is used.

w_{0}(o)=D_{0,R}(o,o)\,

The array of starting overlaps is copied into the array of overlaps at the current position index $o_{x}$ and the listing can start.

Listing

The listing starts at the left boundary $x=0$ and ends at the right boundary $x=l$ . At each increment of the position index one cell is computed for each of the $p$ preimages.

To simplify the algorithem the right cell $x+k-k_{0}-1$ in the neighborhood $n_{x}$ is stored. The first cells $-k_{0}\leq x\leq k-k_{0}-1$ of preimages on a bounded lattice can be computed from the starting overlap $o_{0}$ . For cyclic lattices the last cells at the right can be wraped to the beginning.

Algorithm pseudocode

C = malloc( p * (l+k-1) * |S| )            # reserve memory for the counted amount of preimages
                                           #
i = 0                                      # start with the first preimage
for ( o=0; o<|S|^(k-1); o++ )              # for all overlaps
  for ( j=0; j<b_L[0][o]*b_R[0][o]; i++ )  # for each overlap the number of preimages is calcuated
    o_x[i] = o                             # i-th preimage path begins with overlap o
    i++                                    # to the next preimage
  end_for                                  #
end_for                                    #
if (cyclyc)                                # for bounded lattices there is no need to know the starting points
  o_L = o_R = o_x                          # copy the current array of overlap to the array of starting overlaps
end_if                                     #

for ( x=0; x<l; x++ )                      # run from the left to the right
  i = 0                                    # start with the first preimage
  while ( i< p )                           # check if all preimages have been finished
    for ( c=0; c<|S|; c++)                 # check all links for each source overlap
      o_x[i] = (o_x[i]*|S|+c) / |S|^(k-1)  # calculate the drain overlap
      elseif (bounded)                     # for bounded lattices
        w = b_R[x+1][o_x[i]]               # the count from the drain node to the right end is used
      if (cyclic)                          # for cyclic lattices
        w = D_R[x+1][o_x[i],o_L[i]]        # the count from the drain node to the end node (same as left)
      end_if                               #
      for ( j=0; j<w; j++ )                # use the count
        C[i][x+k-k0-1] = c                 # and write a cell for each of them
        i++                                # increment the preimage counter
      end_for                              #
    end_for                                #
  end_while                                #
end_for                                    # end of algorithm

Algorithm complexity

The complexity of the counting is a linear function of the configuration length $l$ . The dependence on the neighborhood size $k$ is not qubic since there at most $k$ nonzero elements in the preimage matrix of a single cell. If the lattice is bounded the counts are stored as vectors and the complexity is linear, for cyclic lattices counts are stored as vectors and the complexity is quadratic.

T_{count,bounded}=C_{count}lk\,

T_{count,cyclic}=C_{count2}lk^{2}\,

The complexity of the listing is again a linear function of the configuration length $l$ and the number of preimages.

T_{list}=C_{list}l\cdot p

The counting by matrix multiplication processes all the nodes in the primage diagram instead the tracing and backtracking from the previous algorithm avoids some nodes gaining on everage complexity, on the other hand this algorith is easier to optimize.

Memory consumption is another downside, and it grows as fast as time for counting.

Proofs

References

Andrew Wuensche and Mike Lesser, The Global Dynamics of Cellular Automata An Atlas of Basin of Attraction Fields of One-Dimensional Cellular Automata
Wuensche,A.,(1997), Attractor Basins of Discrete Networks, Cognitive Science Research Paper 461, Univ. of Sussex, D.Phil thesis
Vladimir Batagelj, Efficient Algorithms for Citation Network Analysis (2003)
J. C. Seck Tuoh, G. Juárez y H. V. McIntosh, Calculating ancestors in one-dimensional cellular automata, International Journal of Modern Physics C, Vol 15, No. 8, pp 1151-1169, October 2004
MathPages
- Cellular Automata
- Global Reversibility of Cellular Automata
Iztok Jeras, Andrej Dobnikar, Algorithms for computing preimages of cellular automata configurations (PDF)

Software

DDLab Tools for researching Cellular Automata, Random Boolean Networks, multi-value Discrete Dynamical Networks, and beyond; by Andy Wuensche.
Iztok Jeras, Algorithms for computing preimages of cellular automata configurations TAR.BZ2