Circuit Idea/Creating a circuit with negative differential resistance
Why does voltage decrease when current increases?
[edit | edit source]By negative differential resistance, they usually mean a circuit where the current decreases when the voltage increases.
Well, true... But what is the physical meaning of this statement? How does this magic work? Is it something useful and therefore desirable? If so, what can we use it for? Let's understand it thinking as humans and explain it without using meaningless verbal clichés.
Basic idea
[edit | edit source]The purpose of a negative resistor is to do the opposite of what a "positive" resistor does, i.e. to add rather than dissipate power. True negative resistors do this by adding voltage in series or current in parallel from their own built-in sources. But how is the humble resistor to do so when it does not have that? The only thing it has is resistance and that is something that dissipates power.
But wait, it can reduce its resistance and thus increase the power added by an external source! So the idea in general, as we know it from life, is to initially do something bad and then start reducing it, creating the illusion that we are doing good. In this particular case, the negative differential resistor (NDR) has some initial resistance which creates a voltage drop ("bad"). But then it begins to decrease its resistance as the current increases, thus creating the illusion that it is adding power ("good"). Simply put, NDR acts as a dynamic resistor.
NDR acting this way are called "S-shaped" or "current-driven" while the opposite NDR (tunnel diode, lambda diode, etc.) are called "N-shaped" or "voltage-driven".
Let's now explore this phenomenon in detail through step-by-step CircuitLab experiments, first with a "positive" resistor and then with an S-shaped NDR.
I = 1 mA, V = 1 V, R = 1 kΩ

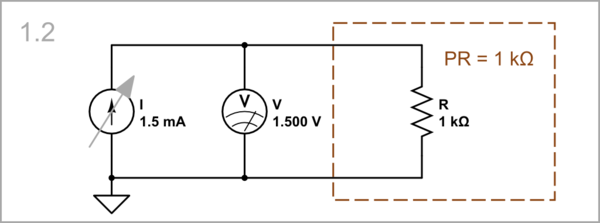
I = 1.5 mA, V = 1.5 V, R = 1 kΩ
I = 2 mA, V = 2 V, R = 1 kΩ

The behavior of a 1 kΩ positive resistor matches our intuition confirmed scientifically by Ohm's law. We can see graphically that when we increase the current through the resistor, the voltage across it increases proportionally, and the resistance does not change (R is static). The resistor IV curve does not move.

Negative differential resistance
[edit | edit source]Conceptual circuit
[edit | edit source]To understand exactly how NDR does this magic, let's simulate it with a variable resistor R.
I = 1 mA, V = 2 V, R = 2 kΩ: Its initial (static) resistance is 2 kΩ but in this static state we cannot say how much NDR is.
I = 1.5 mA, V = 1.5 V, R = 1 kΩ: When the current rises to 500mA, the trick is that we reduce R by 1 kΩ, and the voltage drop instead of rising, drops.

I = 2 mA, V = 1 V, R = 500 Ω: Then the current increases by another 500 mA, but we reduce R by 500 Ω, and the voltage drops even more.

In the graphical representation, when the current increases, the resistor IV curve rotates counterclockwise, and the voltage decreases. The intersection points lie on the -1 kΩ NDR IV curve (in green).

Why voltage decreases when current increases
[edit | edit source]The explanation of this mysterious phenomenon (never done in textbooks) turned out to be very simple:
Basically, Ohm's law is a function of one variable (input quantity) - Vout = Iin.R. So as we increase the input current Iin, the output voltage Vout increases proportionally with the factor R (constant). If we begin to vary the resistance at the same time as the current, Ohm's law becomes a function of two variables (input quantities) - Vout = Iin.Rin. Depending on the rate of change of R, we have the following cases:
- First, if we decrease the resistance at a smaller rate of change than that of the current increase, the voltage will increase but less, and we will have the illusion of lower resistance. An example is a poor quality Zener diode.
- Then, if we decrease the resistance at the same rate of change as the current, the voltage will not change at all, and we will have the illusion of zero resistance. An example is a perfect Zener diode.
- Finally, when we decrease the resistance at a higher rate than that of the current, the voltage starts to change in the opposite direction, and we think of it as a negative resistance. An example is a neon lamp.
