Circuit Idea/How to make an element with true negative resistance?

This story is based on an answer to an SE EE question.

The secret of negative resistance

There are two types of negative resistance - true (absolute) and differential. Both are dynamic devices whose parameters depend on the input value, but the former are sources while the latter are resistors that need sources. It seems that the true negative resistance is more easy to understand so it will be considered here. We will see that despite the "mysticism" with which it is surrounded, it is a very simple and intuitive concept.

Both "positive" and negative resistors are two terminal devices with linear relationship between voltage and current (Ohm's law). But while an ordinary "positive" resistor subtracts voltage from the supply voltage, the so-called voltage-inversion negative impedance converter (VNIC) adds voltage to it; while an ordinary resistor draws current from the supply voltage, the current-inversion negative impedance converter (INIC) injects current to it. This is the meaning of the negative sign before V or I.

The benefit of negative resistance is that it can neutralize equivalent positive resistance. Both NICs "help" the main source - VNIC "helps" a voltage source in series; INIC "helps" a current source in parallel. Figuratively speaking, they "eat" some of the positive resistance, and what remains is only positive resistance. The best way to see how this can be done is to consider some basic applications. Two interesting of them are chosen - improving an imperfect ammeter and voltmeter to make them "ideal".

Making an "ideal" ammeter with VNIC

Voltage source supplies a resistor

Imagine that we want to measure the current in the simple Ohm's circuit below.

The schematic represents a voltage-controlled Ohm's circuit

Simulate this circuit – Schematic created using CircuitLab

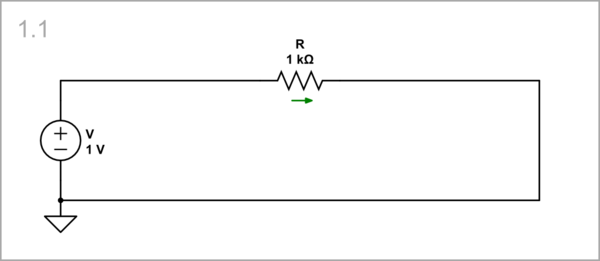
Measuring the current by a perfect ammeter

For this purpose, we can include a perfect ammeter AM with zero internal resistance; its reading is as we expected 1 mA. Also, to measure the voltage drop across the resistor R without complicating the circuit, let's replace the resistor by an imperfect voltmeter VM1k with 1 kΩ internal resistance (we can set it in the voltmeter parameters window). Figuratively speaking, it will be a "voltage-visualized resistor".

The schematic represents a voltage-controlled Ohm's circuit with an "ideal" ammeter

Simulate this circuit

Measuring the current by an imperfect ammeter

However, our goal is to convert the "bad" ammeter into a "very good one". Therefore, we first deliberately "degrade" it (as we did with the voltmeter above) by giving it a resistance of 1 kΩ; as a result, the current decreases twice. Then, we start thinking about how to improve it (but in our own way, not through CircuitLab). Indeed, there is something comical about the fact that we have a perfect ammeter that we "ruin", and then make it perfect again:-) but we do it for the purposes of the good explaining. This is a typical didactic trick that can be useful when explaining circuits.

The schematic represents a voltage-controlled Ohm's circuit with an imperfect ammeter

Simulate this circuit

Compensating the ammeter voltage drop by a constant voltage source

Since voltage is lost in the ammeter, we guess to add the same voltage in the circuit. Great idea! To implement it, we connect another voltage source R-1k in series with the ammeter, and set its voltage equal to the voltage drop across the ammeter. As a result, the ammeter voltage drop is neutralized, and the string of the two devices in series - AM1k and R-1k, behaves as an "ideal" ammeter with zero resistance and zero voltage! The 1 mA current is determined, according to Ohm's law, only by the 1 V input voltage and the 1 kΩ voltmeter's resistance.

The schematic represents a voltage-controlled Ohm's circuit where the undesired ammeter voltage drop is compensated by a constant voltage source

Simulate this circuit

Compensating the voltage drop by a following voltage source

But this trick only works for one input voltage value. So we need to make it continuously follow the ammeter's voltage. For this purpose, we can replace it with a varying "copying" source R-1 which is controlled by the same current (current-to-voltage converter). In CircuitLab, it can be implemented as the so-called "behavioral voltage source" with a voltage VR-1 = 1000.IAM1k. Figuratively speaking, it behaves as a negative resistor with the same but negative resistance of -1 kΩ so the combination of the two devices always has zero total resistance.

The schematic represents a voltage-controlled Ohm's circuit where the undesired ammeter voltage drop is compensated by a constant voltage source

Simulate this circuit

It turns out that CircuitLab allows negative resistance values to be set. Then let's simplify the conceptual schematic even more.

The schematic represents a voltage-controlled Ohm's circuit where the undesired ammeter voltage drop is compensated by a constant voltage source

Simulate this circuit

Compensating the voltage drop by VNIC

VNICs are made the same way as the negative resistance compensation above - by adding (but twice as much) negative resistance to positive resistance (R - 2R = -R). The idea of this is as follows.

Conceptual circuit: To produce a negative resistance, the converter needs a positive resistance to copy the voltage drop across it; hence the name "negative impedance converter". However, it must then remove this positive resistance so that only negative resistance remains that destroys the undesired ammeter resistance (R + R - 2R = 0). So the behavioral voltage source now produces two times higher voltage VR-2 = 2.1000.IAM1k. Note the opposite voltage polarity (hence the name "voltage-inversion NIC").

The schematic represents a voltage-controlled Ohm's circuit where the undesired ammeter voltage drop is compensated by an VNIC

Simulate this circuit

Practical circuit: To implement this powerful idea by an op-amp circuit, we pass the current through the 1 kΩ "original" resistor R1, amplify the voltage drop across it by an "little unusual" op-amp non-inverting amplifier (OA, R2 and R3), and sum the two voltages. Since the currents flowing through R1 and R2 are the same, the voltage drops are I.R1 - I.R2 - I.R3 -> V - V -V = -V. So, the circuit produces a voltage equal to the voltage drop across the ammeter but with the opposite sign, i.e., it behaves as a -1 kΩ negative resistor. The result is zero voltage drop and zero resistance ("virtual short").

The schematic represents a voltage-controlled Ohm's circuit where the undesired ammeter voltage drop is compensated by an op-amp VNIC

Simulate this circuit

Making an "ideal" voltmeter with INIC

Now let's consider the dual, no less interesting NIC application.

Voltage source with a resistor in series

Imagine that we want to measure the output voltage of an imperfect voltage source with 1 kΩ internal resistance R.

The schematic represents an imperfect voltage source with no load connected

Simulate this circuit

Measuring the voltage by a perfect voltmeter

For this purpose, we can connect a perfect voltmeter VM with infinitely high internal resistance; its reading is as we expected 1 V since there no current flows. Also, to measure the current flowing through the resistor R later without complicating the circuit, let's replace the resistor by an imperfect ammeter AM1k with 1 kΩ internal resistance (the same trick as above). Thus it will be a "current-visualized resistor".

The schematic represents an imperfect voltage source with no load connected

Simulate this circuit

Measuring the voltage by an imperfect voltmeter

However, our goal is to convert a "bad" voltmeter into a "very good" one. Therefore, we first deliberately "degrade" it (as we did with the ammeter above) by giving it a resistance of 1 kΩ, and start thinking about how to improve it (but in our own way, not through CircuitLab).

The schematic represents an imperfect voltmeter connected to an imperfect voltage source

Simulate this circuit

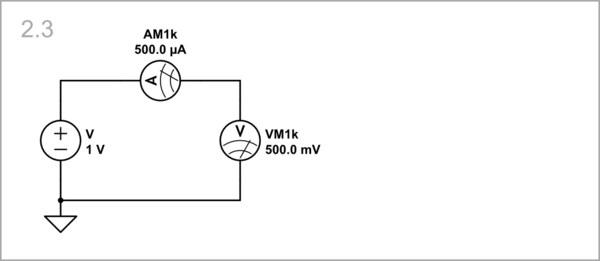
Compensating the voltmeter current by a constant current source

Since some current is consumed by the voltmeter, we guess to apply the same trick as above - to add the same current to the circuit. Really great idea! To implement it, here we connect another current source R-1k in parallel to the voltmeter and set its current equal to the current consumed by the voltmeter. As a result, the latter is neutralized and the combination of the two devices - VM1k and R-1k, behaves as an "ideal" voltmeter with infinite resistance and zero current! As you can see, no current is consumed by the voltage source, and the current through the "bad" voltmeter is entirely provided by the additional current source.

The schematic represents an imperfect voltmeter connected to an imperfect voltage source

Simulate this circuit

Compensating the current by a following current source

But this trick only works for one input voltage value. So we need to make the "helping" current source continuously follow the voltmeter's voltage. For this purpose, we can replace it with a varying current source which is controlled by the same voltage (voltage-to-current converter). In CircuitLab, it can be implemented as a "behavioral current source" producing current IR-1k = VR1k/1000. It behaves as a negative resistor with the same but negative resistance of -1 kΩ so the combination of the two devices always has infinite total resistance.

The schematic represents compensating the current by a following current source.png

Simulate this circuit

Let's again take advantage of CircuitLab's ability to set negative resistаnce values and simplify the conceptual schematic even more.

The schematic represents compensating the voltmeter current by a negative resistance

Simulate this circuit

Compensating the current by INIC

Conceptual circuit: The converter contains a behavioral voltage source that produces two times higher voltage than the voltage across the imperfect voltmeter - V-2k = 2.VM1k. Then it is converted by the 1 kΩ resistance R1k into a current with reversed direction (it enters instead to exit the imperfect voltmeter); hence the name "current-inversion negative impedance converter".

The schematic represents compensating the current by INIC (conceptual circuit)

Simulate this circuit

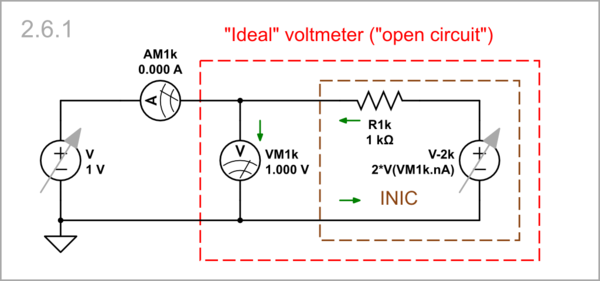
Practical circuit: To implement this powerful idea by an op-amp circuit, we amplify twice the voltage across the voltmeter by a classic op-amp non-inverting amplifier (OA, R2 and R3), and apply it through the 1 kΩ resistor R1 back to the imperfect voltmeter. So, the circuit produces all the current needed for the imperfect voltmeter. No current is consumed by the voltage source as though there is no load connected ("virtual open circuit").

The schematic represents compensating the current by INIC (practical circuit)

Simulate this circuit

Conclusions

We have to decide what kind of negative resistor (NIC) we need:

• If we intend to compensate for losses in a resistor connected in series to a voltage source, we need a VNIC.
• If we intend to compensate for losses in a resistor connected in parallel to a current source, we need an INIC.
• If we look carefully at VNIC and INIC circuit diagrams, we will find that both contain "doubling voltage sources" (non-inverting amplifiers with a gain of 2) but they are used differently:

• VNIC adds its voltage to the input voltage,
• INIC subtracts its voltage from the input voltage,
• but because they are connected differently (VNIC in series and INIC in parallel) to the input sources, both "help" them.

External links

How to make an element with true negative resistance? SE EE question and answer