Data Structures/Trees

Data Structures
Introduction - Asymptotic Notation - Arrays - List Structures & Iterators
Stacks & Queues - Trees - Min & Max Heaps - Graphs
Hash Tables - Sets - Tradeoffs

Trees

A tree is a non-empty set with an element that is designated as the root of the tree while the remaining elements are partitioned into non-empty sets each of which is a subtree of the root.

Tree nodes have many useful properties. The depth of a node is the length of the path (or the number of edges) from the root to that node. The height of a node is the longest path from that node to its leaves. The height of a tree is the height of the root. A leaf node has no children—its only path is up to its parent.

See the axiomatic development of trees and its consequences for more information.

Types of trees:

Binary: Each node has zero, one, or two children. This assertion makes many tree operations simple and efficient.

Binary Search: A binary tree where any left child node has a value less than its parent node and any right child node has a value greater than or equal to that of its parent node.

Traversal

Many problems require we visit the nodes of a tree in a systematic way: tasks such as counting how many nodes exist or finding the maximum element. Three different methods are possible for binary trees: preorder, postorder, and in-order, which all do the same three things: recursively traverse both the left and right subtrees and visit the current node. The difference is when the algorithm visits the current node:

preorder: Current node, left subtree, right subtree (DLR)

postorder: Left subtree, right subtree, current node (LRD)

in-order: Left subtree, current node, right subtree (LDR)

levelorder: Level by level, from left to right, starting from the root node.

• Visit means performing some operation involving the current node of a tree, like incrementing a counter or checking if the value of the current node is greater than any other recorded.

Sample implementations for Tree Traversal

preorder(node)
 visit(node)
 if node.left ≠ null then preorder(node.left)
 if node.right ≠ null then preorder(node.right)

inorder(node)
 if node.left ≠ null then inorder(node.left)
 visit(node)
 if node.right ≠ null then inorder(node.right)

postorder(node)
 if node.left ≠ null then postorder(node.left)
 if node.right ≠ null then postorder(node.right)
 visit(node)

levelorder(root)
 queue<node> q
 q.push(root)
 while not q.empty do
  node = q.pop
  visit(node)
  if node.left ≠ null then q.push(node.left)
  if node.right ≠ null then q.push(node.right)

For an algorithm that is less taxing on the stack, see Threaded Trees.

Examples of Tree Traversals

preorder: 50,30, 20, 40, 90, 100
inorder: 20,30,40,50, 90, 100
postorder: 20,40,30,100,90,50

Balancing

When entries that are already sorted are stored in a tree, all new records will go the same route, and the tree will look more like a list (such a tree is called a degenerate tree). Therefore the tree needs balancing routines, making sure that under all branches are an equal number of records. This will keep searching in the tree at optimal speed. Specifically, if a tree with n nodes is a degenerate tree, the longest path through the tree will be n nodes; if it is a balanced tree, the longest path will be log n nodes.

Algorithms/Left rotation: This shows how balancing is applied to establish a priority heap invariant in a Treap, a data structure which has the queueing performance of a heap, and the key lookup performance of a tree. A balancing operation can change the tree structure while maintaining another order, which is binary tree sort order. The binary tree order is left to right, with left nodes' keys less than right nodes' keys, whereas the priority order is up and down, with higher nodes' priorities greater than lower nodes' priorities. Alternatively, the priority can be viewed as another ordering key, except that finding a specific key is more involved.

The balancing operation can move nodes up and down a tree without affecting the left right ordering.

AVL: A balanced binary search tree according to the following specification: the heights of the two child subtrees of any node differ by at most one.

Red-Black Tree: A balanced binary search tree using a balancing algorithm based on colors assigned to a node, and the colors of nearby nodes.

AA Tree: A balanced tree, in fact a more restrictive variation of a red-black tree.

Binary Search Trees

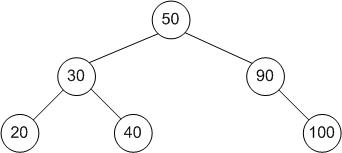
A typical binary search tree looks like this:

Terms

Node Any item that is stored in the tree. Root The top item in the tree. (50 in the tree above) Child Node(s) under the current node. (20 and 40 are children of 30 in the tree above) Parent The node directly above the current node. (90 is the parent of 100 in the tree above) Leaf A node which has no children. (20 is a leaf in the tree above)

Searching through a binary search tree

To search for an item in a binary tree:

1. Start at the root node
2. If the item that you are searching for is less than the root node, move to the left child of the root node, if the item that you are searching for is more than the root node, move to the right child of the root node and if it is equal to the root node, then you have found the item that you are looking for.
3. Now check to see if the item that you are searching for is equal to, less than or more than the new node that you are on. Again if the item that you are searching for is less than the current node, move to the left child, and if the item that you are searching for is greater than the current node, move to the right child.
4. Repeat this process until you find the item that you are looking for or until the node does not have a child on the correct branch, in which case the tree doesn't contain the item which you are looking for.

Example

For example, to find the node 40...

1. The root node is 50, which is greater than 40, so you go to 50's left child.
2. 50's left child is 30, which is less than 40, so you next go to 30's right child.
3. 30's right child is 40, so you have found the item that you are looking for :)

.........

Adding an item to a binary search tree

1. To add an item, you first must search through the tree to find the position that you should put it in. You do this following the steps above.
2. When you reach a node which doesn't contain a child on the correct branch, add the new node there.

For example, to add the node 25...

1. The root node is 50, which is greater than 25, so you go to 50's left child.
2. 50's left child is 30, which is greater than 25, so you go to 30's left child.
3. 30's left child is 20, which is less than 25, so you go to 20's right child.
4. 20's right child doesn't exist, so you add 25 there :)

Deleting an item from a binary search tree

It is assumed that you have already found the node that you want to delete, using the search technique described above.

Case 1: The node you want to delete is a leaf

For example, to delete 40...

• Simply delete the node!

Case 2: The node you want to delete has one child

1. Directly connect the child of the node that you want to delete, to the parent of the node that you want to delete.

For example, to delete 90...

• Delete 90, then make 100 the child node of 50.

Case 3: The node you want to delete has two children

One non-standard way, is to rotate the node into a chosen subtree, and attempt to delete the key again from that subtree, recursively, until Case 1 or Case 2 occurs. This could unbalance a tree, so randomly choosing whether to right or left rotate may help.

The standard way is to pick either the left or right child, say the right, then get the right's leftmost descendent by following left ,starting from the right child, until the next left is null. Then remove this leftmost descendant of the right child, replacing it with its right sub-tree ( it has a left child of null). Then use the contents of this former leftmost descendant of the right child, as replacement for the key and value of the node being deleted , so that its values now are in the deleted node, the parent of the right child. This still maintains the key ordering for all nodes. Example java code is below in the treap example code.

The following examples use the standard algorithm, that is, the successor is the left-most node in the right subtree of the node to be deleted.

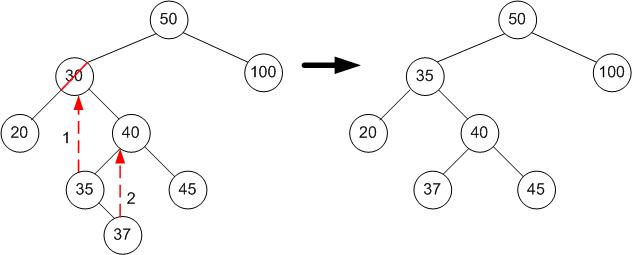
For example, to delete 30

1. The right node of the node which is being deleted is 40.
2. (From now on, we continually go to the left node until there isn't another one...) The first left node of 40, is 35.
3. 35 has no left node, therefore 35 is the successor!
4. 35 replaces 30, at the original right node, and the node with 35 is deleted, replacing it with the right sub-tree, which has the root node 37.

Case 1 of two-children case: The successor is the right child of the node being deleted

1. Directly move the child to the right of the node being deleted into the position of the node being deleted.
2. As the new node has no left children, you can connect the deleted node's left subtree's root as it's left child.

For example, to delete 30

1. replace the contents to be deleted (30), with the successor's contents( 40).
2. delete the successor node (contents 40), replacing it with its right subtree (head contents 45).

Case 2 of two-children case: The successor isn't the right child of the node being deleted

This is best shown with an example

To delete 30...

1. Replace the contents to be deleted (30) with the successor's contents (35).
2. replace the successor (35) with it's right subtree (37). There is no left subtree because the successor is leftmost.

Example extract of Java code for binary tree delete operation

private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
 
		if (node == null) {
			return null;
		} else if (k.compareTo(node.k) < 0) {
			 node.left = deleteNode(k, node.left, del);
		} else if (k.compareTo(node.k) > 0) {
			node.right = deleteNode(k, node.right, del);
 
			// k.compareTo(node.k) == 0
		} else if ( node.left == null ) {
				del.success = true;
				return node.right;
		} else if ( node.right == null) {
			  del.success = true;
				return node.left;
		} else if (node.left !=null && node.right != null){
		/*
        // non-standard method,
		// left rotate and all delete on left subtree

			TreapNode tmp = node.right;
			node.right = node.right.left;
		    tmp.left = node;
		    node = tmp;			
			node.left = deleteNode(k , node.left, del);
			
         */

	    // more standard method ? doesn't disturb tree structure as much
	    // find leftmost descendant of the right child node and replace contents

			TreapNode n2 = node.right;
			TreapNode previous2 = null;
			while (n2.left != null) {
				previous2 = n2;
				n2 = n2.left;
			}
 
			if (previous2 != null) {
				previous2.left = n2.right;
                //n2 has no parent link, orphaned
			} else {
				node.right = n2.right;
                //n2 has no parent link, orphaned
			}
 
			node.k = n2.k;
			node.val = n2.val;
			del.success = true;
            // once n2 out of scope, the orphaned node at n2 will be garbage collected, 
		}
 
		return node;
	}

Red-Black trees

A red-black tree is a self-balancing tree structure that applies a color to each of its nodes. The structure of a red-black tree must adhere to a set of rules which dictate how nodes of a certain color can be arranged. The application of these rules is performed when the tree is modified in some way, causing the rotation and recolouring of certain nodes when a new node is inserted or an old node is deleted. This keeps the red-black tree balanced, guaranteeing a search complexity of O(log n).

The rules that a red-black tree must adhere to are as follows:

1. Each node must be either red or black.
2. The root is always black.
3. All leaves within the tree are black (leaves do not contain data and can be modelled as null or nil references in most programming languages).
4. Every red node must have two black child nodes.
5. Every path from a given node to any of its descendant leaves must contain the same number of black nodes.

A red-black tree can be modelled as 2-3-4 tree , which is a sub-class of B tree (below). A black node with one red node can be seen as linked together as a 3-node , and a black node with 2 red child nodes can be seen as a 4-node.

4-nodes are split , producing a two node, and the middle node made red, which turns a parent of the middle node which has no red child from a 2-node to a 3-node, and turns a parent with one red child into a 4-node (but this doesn't occur with always left red nodes).

A in-line arrangement of two red nodes, is rotated into a parent with two red children, a 4-node, which is later split, as described before.

   A right rotate      'split 4-node'  |red
 red / \  -->    B      --->  B
  B        red/ \red        / \
red / \        C  A        C  A
 C  D         /          /
           D          D

An optimization mentioned by Sedgewick is that all right inserted red nodes are left rotated to become left red nodes, so that only inline left red nodes ever have to be rotated right before splitting. AA-trees (above) by Arne Anderson , described in a paper in 1993 , seem an earlier exposition of the simplification, however he suggested right-leaning 'red marking' instead of left leaning , as suggested by Sedgewick, but AA trees seem to have precedence over left leaning red black trees. It would be quite a shock if the Linux CFS scheduler was described in the future as 'AA based'.

In summary, red-black trees are a way of detecting two insertions into the same side, and levelling out the tree before things get worse . Two left sided insertions will be rotated, and the two right sided insertions, would look like two left sided insertions after left rotation to remove right leaning red nodes. Two balanced insertions for the same parent could result in a 4-node split without rotation, so the question arises as to whether a red black tree could be attacked with serial insertions of one sided triads of a < P < b , and then the next triad's P' < a.

Python illustrative code follows

RED = 1
BLACK = 0
class Node:
 def __init__(self, k, v):
  # all newly inserted node's are RED 
  self.color = RED
  self.k = k
  self.v = v
  self.left = None
  self.right = None

class RBTree:
 def __init__(self):
  self.root = None

 def insert(self, k, v) :
  self.root = self._insert(self.root, k,v)

 def _insert(self, n , k, v):
	if n is None:
		return Node(k,v)
	if k < n.k :
		n.left = self._insert(n.left, k , v)
  elif k > n.k :
		n.right = self._insert(n.right, k, v)
  if n.right.color is RED:
		#always on the left red's
		#left rotate
		tmp = n.right
		n.right = tmp.left
		tmp.left = n
		n = tmp

    #color rotation is actually a swap
		tmpcolor = n.color
		n.color = n.left.color
		n.left.color = tmpcolor
			
	if n.left <> None and n.left.left <> None and n.left.left.color == RED and n.left.color == RED:
		# right rotate in-line reds
		print "right rotate"
		tmp = n.left
		n.left = tmp.right
		tmp.right = n
		n = tmp

        #color rotation is actually a swap
		tmpcolor = n.color
		n.color = n.right.color
		n.right.color = tmpcolor

		if n.left <> None: print n.left.color, n.color, n.right.color

	#no need to test, because after right rotation, will need to split 3-node , as right rotation has
    #brought red left grandchild to become left red child, and left red child is now red right child
    #so there are two red children.

    #if n.left <> None and n.right <> None and n.left.color == RED and n.right.color == RED:
		print "split"
		n.color = RED
		n.left.color = BLACK
		n.right.color = BLACK

	return n

 def find(self, k):
	return self._find_rb(k, self.root)

 def _find_rb(self, k, n):
	if n is None:
		return None
	if k < n.k:
		return self._find_rb( k, n.left)
	if k > n. k:
		return self._find_rb( k, n.right)
	return n.v
	
 def inorder(self):
	self.inorder_visit(self.root, "O")

 def inorder_visit(self, node,label=""):
	if node is None: return
	self.inorder_visit(node.left, label+"/L")
	print label, "val=", node.v
	self.inorder_visit(node.right, label+"/R")
	

def test1(N):
    t = RBTree() 	
	for i in xrange(0,N):
     t.insert(i,i)

	l = []		
	t.inorder()
	for i in xrange(0,N):
     x =t.find(i)
     if x <> None:
		 l.append((x, i) )
	print "found", len(l) 
   
if __name__ == "__main__":
	import random
	test1(100000)
	test1(1000)
	test1(100)
	test1(10)

B Trees

Summary

• Whereas binary trees have nodes that have two children, with the left child and all of its descendants less than the "value" of the node, and the right child and all of its children more than the "value" of the node, a B-tree is a generalization of this.
• The generalization is that instead of one value, the node has a list of values, and the list is of size n ( n > 2 ). n is chosen to optimize storage , so that a node corresponds in size to a block for instance. This is in the days before ssd drives, but searching binary nodes stored on ssd ram would still be slower than searching ssd ram for a block of values, loading into normal ram and cpu cache, and searching the loaded list.
• At the start of the list, the left child of the first element of the list has a value less than the first element , and so do all its children. To the right of the first element, is a child which has values more than the first element's value, as do all of its children, but also less than the value of the second element. Induction can be used , and this holds so for the child between element 1 and 2, 2 and 3, ... so on until n-1 and nth node.
• To insert into a non-full B tree node, is to do a insertion into a sorted list.
• In a B+ tree, insertions can only be done in leaf nodes, and non-leaf nodes hold copies of a demarcating value between adjacent child nodes e.g. the left most value of an element's right child's list of nodes.
• Whenever a list becomes full e.g. there are n nodes, the node is "split", and this means making two new nodes, and passing the demarcating value upto the parent.

B Trees were described originally as generalizations of binary search trees , where a binary tree is a 2-node B-Tree, the 2 standing for two children, with 2-1 = 1 key separating the 2 children. Hence a 3-node has 2 values separating 3 children, and a N node has N children separated by N-1 keys.

A classical B-Tree can have N-node internal nodes, and empty 2-nodes as leaf nodes, or more conveniently, the children can either be a value or a pointer to the next N-node, so it is a union.

The main idea with B-trees is that one starts with a root N-node , which is able to hold N-1 entries, but on the Nth entry, the number of keys for the node is exhausted, and the node can be split into two half sized N/2 sized N nodes, separated by a single key K, which is equal to the right node's leftmost key, so any entry with key K2 equal or greater than K goes in the right node, and anything less than K goes in the left. When the root node is split, a new root node is created with one key, and a left child and a right child. Since there are N children but only N-1 entries, the leftmost child is stored as a separate pointer. If the leftmost pointer splits, then the left half becomes the new leftmost pointer, and the right half and separating key is inserted into the front of the entries.

An alternative is the B+ tree which is the most commonly used in database systems, because only values are stored in leaf nodes, whereas internal nodes only store keys and pointers to other nodes, putting a limit on the size of the datum value as the size of a pointer. This often allows internal nodes with more entries able to fit a certain block size, e.g. 4K is a common physical disc block size. Hence , if a B+ tree internal node is aligned to a physical disc block, then the main rate limiting factor of reading a block of a large index from disc because it isn't cached in a memory list of blocks is reduced to one block read.

A B+ tree has bigger internal nodes, so is wider and shorter in theory than an equivalent B tree which must fit all nodes within a given physical block size, hence overall it is a faster index due to greater fan out and less height to reach keys on average.

Apparently, this fan out is so important, compression can also be applied to the blocks to increase the number of entries fitting within a given underlying layer's block size (the underlying layer is often a filesystem block).

Most database systems use the B+ tree algorithm, including postgresql, mysql, derbydb, firebird, many Xbase index types, etc.

Many filesystems also use a B+ tree to manage their block layout (e.g. xfs, NTFS, etc).

Transwiki has a java implementation of a B+ Tree which uses traditional arrays as key list and value list.

Below is an example of a B Tree with test driver, and a B+ tree with a test driver. The memory / disc management is not included, but a usable hacked example can be found at Hashing Memory Checking Example.

This B+ tree implementation was written out of the B Tree , and the difference from the transwiki B+ tree is that it tries to use the semantics of SortedMap and SortedSet already present in the standard Java collections library.

Hence , the flat leaf block list of this B+ implementation can't contain blocks that don't contain any data, because the ordering depends on the first key of the entries, so a leaf block needs to be created with its first entry.

A B tree java example

package btreemap;

import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.TreeMap;

/** can't work without setting a comparator */
public class BTreeMap<K, V> implements SortedMap<K, V> {

	private static final int NODE_SIZE = 100;
	
	

	@Override
	public Comparator<? super K> comparator() {
		// TODO Auto-generated method stub

		return comparator;
	}

	Comparator< ? super K> defaultComparator = new
	Comparator< K>() {

		@Override
		public int compare(K o1, K o2) {
			// TODO Auto-generated method stub
			Comparable c1 = (Comparable)o1;
			Comparable c2 = (Comparable)o2;
			return c1.compareTo(c2);
		}
	};
	Comparator<? super K> comparator = defaultComparator;
	BTBlock<K, V> root = new BTBlock<K, V>(NODE_SIZE, comparator);
	/**
	 * 
	 * @param comparator
	 *      - this is mandatory for the tree to work
	 */
	public void setComparator(Comparator<? super K> comparator) {
		this.comparator = comparator;
		root = new BTBlock<K, V>(NODE_SIZE, comparator);
	}

	/**
	 * 
	 * 
	 * 
	 * @param <K>
	 * @param <V>
	 *      the entry is associated with a right child block.
	 * 
	 */
	static class BlockEntry<K, V> {
		K k;
		V v;
		BTBlock left;

		BlockEntry() {

		}

		BlockEntry(K k, V v) {
			left = null;
			this.k = k;
			this.v = v;
		}
	}

	/**
	 * 
	 * - this represents the result of splitting a full block into
	 *     a left block, and a right block, and a median key, the right
	 *     block and the median key held in a BlockEntry structure as above.
	 * @param <K>
	 * @param <V>
	 * @param <V>g
	 */
	static class SplitRootEntry<K, V> {
		BTBlock<K, V> right;
		BlockEntry<K, V> entry;

		SplitRootEntry(BlockEntry<K, V> entry, BTBlock<K, V> right) {
			this.right = right;
			this.entry = entry;
		}

		SplitRootEntry() {
			super();
		}
	}

	/**
	 * this is used to return a result of a possible split , during recursive
	 * calling.
	 * 
	 * 
	 * 
	 * @param <K>
	 * @param <V>
	 */
	static class resultAndSplit<K, V> {

		/**
		 * null , if there is no split.
		 */
		SplitRootEntry<K, V> splitNode;
		V v;

		resultAndSplit(V v) {
			this.v = v;
		}

		resultAndSplit(SplitRootEntry<K, V> entry, V v) {
			this.v = v;
			this.splitNode = entry;
		}
	}

	/**
	 * used to represent the insertion point after searching a block if compare
	 * is zero, then a match was found, and pos is the insertion entry if
	 * compare < 0 and pos == 0 , then the search ended up less than the
	 * leftmost entry else compare > 0 , and the search will be to the immediate
	 * right of pos.
	 * 
	 * 
	 * 
	 */
	static class PosAndCompare {
		int pos = 0;
		int compare = 0;
	}

	static class BTBlock<K, V> {
		List<BlockEntry<K, V>> entries;
		BTBlock<K, V> rightBlock = null;
		private int maxSz = 0;

		Comparator<? super K> comparator;

		Comparator<? super K> comparator() {
			return comparator;
		}

		public BTBlock(int size, Comparator<? super K> c) {
			entries = new ArrayList<BlockEntry<K, V>>();
			maxSz = size;
			this.comparator = c;
		}

		/**
		 * PosAndCompare usage: if compare is zero, then a match was found, and
		 * pos is the insertion entry if compare < 0 and pos == 0 , then the
		 * search ended up less than the leftmost entry else compare > 0 , and
		 * the search will be to the immediate right of pos.
		 * 
		 * 
		 * 
		 */
		// private void blockSearch(K k, PosAndCompare pc) {
		// for (int i = 0; i < entries.size(); ++i) {
		// pc.compare = comparator.compare(k, entries.get(i).k);
		// if (pc.compare == 0) {
		// pc.pos = i;
		// return;
		// }
		// if (pc.compare < 0 && i == 0) {
		// pc.pos = 0;
		// return;
		// }
		//
		// if (pc.compare < 0) {
		// pc.pos = i - 1;
		// pc.compare = 1;
		// return;
		// }
		//
		// }
		// pc.pos = entries.size() - 1;
		// pc.compare = 1;
		//
		// // binary search, it's hard to get it right !
		// // int left = 0;
		// // int right = entries.size();
		// //
		// // while (left <= right && left < entries.size()) {
		// // // pc.pos = (right - left) / 2 + left;
		// // pc.pos = (left + right) / 2;
		// // pc.compare = comparator().compare(k, entries.get(pc.pos).k);
		// // if (pc.compare < 0) {
		// // right = pc.pos - 1;
		// // } else if (pc.compare > 0) {
		// // left = pc.pos + 1;
		// // } else {
		// // return;
		// // }
		// // }
		// //
		// // BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
		// // pc.pos = Collections.binarySearch(entries, e, cmp);
		//
		// }

		Comparator<BlockEntry<K, V>> cmp = new Comparator<BlockEntry<K, V>>() {

			@Override
			public int compare(BlockEntry<K, V> o1, BlockEntry<K, V> o2) {
				// TODO Auto-generated method stub
				return comparator.compare(o1.k, o2.k);

			}
		};

		resultAndSplit<K, V> put(K k, V v) {
			V v2;
			if (entries.size() == 0) {
				entries.add(new BlockEntry<K, V>(k, v));
				return new resultAndSplit<K, V>(v);
			} else {

				// PosAndCompare pc = new PosAndCompare();
				BlockEntry<K, V> e = new BlockEntry<K, V>(k, v);
				int res = Collections.binarySearch(entries, e, cmp);
				int index = -res - 1;
				// blockSearch(k, pc);

				// a match
				if (res >= 0) {
					v2 = entries.get(res).v;
					entries.get(res).v = v;
					return new resultAndSplit<K, V>(v2);
				}

				// follow leftBlock if search is to left of first entry

				if (index == entries.size() && rightBlock != null) {

					resultAndSplit<K, V> result = rightBlock.put(k, v);
					if (result.splitNode != null) {
						rightBlock = result.splitNode.right;
						entries.add(result.splitNode.entry);
					}
				} else if (index == entries.size() && rightBlock == null
						&& entries.size() == maxSz) {
					rightBlock = new BTBlock<K, V>(this.maxSz, comparator);
					resultAndSplit<K, V> result = rightBlock.put(k, v);

				} else if (index < entries.size()
						&& entries.get(index).left != null) {
					// follow right block if it exists
					resultAndSplit<K, V> result = entries.get(index).left.put(
							k, v);
					if (result.splitNode != null) {
						entries.get(index).left = result.splitNode.right;
						// add to the left
						entries.add(index, result.splitNode.entry);

					}

				} else {
					// add to the left
					entries.add(index, e);

				}

				// check if overflowed block , split if it has.
				if (entries.size() > maxSz) {
					int mid = entries.size() / 2;

					// copy right half to new entries list.
					List<BlockEntry<K, V>> leftEntries = new ArrayList<BlockEntry<K, V>>();
					for (int i = 0; i < mid; ++i) {
						leftEntries.add(entries.get(i));
					}

					BlockEntry<K, V> centreEntry = entries.get(mid);

					BTBlock<K, V> leftBlock = new BTBlock<K, V>(maxSz,
							comparator);

					leftBlock.entries = leftEntries;

					// the median entry's left block is the new left block's
					// leftmost block
					leftBlock.rightBlock = centreEntry.left;
					// the new right block becomes the right block
					centreEntry.left = leftBlock;

					// reduce the old block's entries into its left half of
					// entries.
					ArrayList<BlockEntry<K, V>> newEntries = new ArrayList<BlockEntry<K, V>>();
					for (int i = mid + 1; i < entries.size(); ++i)
						newEntries.add(entries.get(i));
					this.entries = newEntries;
					// create a return object, with the reduced old block as the
					// left block
					// and the median entry with the new right block attached

					SplitRootEntry<K, V> split = new SplitRootEntry<K, V>(
							centreEntry, this);

					// the keyed value didn't exist before , so null
					return new resultAndSplit<K, V>(split, null);

				}
				return new resultAndSplit<K, V>(v);
			}

		}

		V get(K k) {

			if (entries.size() == 0)
				return null;

			BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
			int res = Collections.binarySearch(entries, e, cmp);
			int index = -res - 1;

			if (res >= 0) {
				return entries.get(res).v;
			}

			if (index == entries.size() && rightBlock != null) {
				return rightBlock.get(k);
			} else if (index < entries.size()
					&& entries.get(index).left != null) {
				return (V) entries.get(index).left.get(k);
			} else
				return null;
		}

		void getRange(SortedMap map, K k1, K k2) {
			BlockEntry<K, V> e = new BlockEntry<K, V>(k1, null);
			int res = Collections.binarySearch(entries, e, cmp);
			int index = -res - 1;
			BlockEntry<K, V> e2 = new BlockEntry<K, V>(k2, null);
			int res2 = Collections.binarySearch(entries, e2, cmp);
			int index2 = -res2 - 1;

			int from = res >= 0 ? res : index;
			int to = res2 >= 0 ? res2 : index2;

			for (int i = from; i <= to; ++i) {

				if (i < entries.size() && (i > from || res < 0)
						&& entries.get(i).left != null) {
					entries.get(i).left.getRange(map, k1, k2);
					// if (pc2.pos == pc.pos)
					// break;
				}
				if (i < to || res2 >= 0)
					map.put(entries.get(i).k, entries.get(i).v);

				if (i == entries.size() && rightBlock != null) {
					rightBlock.getRange(map, k1, k2);
				}

			}

		}

		K headKey() {
			if (rightBlock != null) {
				return rightBlock.headKey();
			}
			return entries.get(0).k;
		}

		K tailKey() {
			int i = entries.size() - 1;
			if (entries.get(i).left != null) {
				return (K) entries.get(i).left.tailKey();
			}
			return entries.get(i).k;
		}

		void show(int n) {
			showTabs(n);
			for (int i = 0; i < entries.size(); ++i) {
				BlockEntry<K, V> e = entries.get(i);
				System.err.print("#" + i + ":(" + e.k + ":" + e.v + ") ");
			}
			System.err.println();
			showTabs(n);

			if (rightBlock != null) {
				System.err.print("Left Block\n");
				rightBlock.show(n + 1);
			} else {
				System.err.println("No Left Block");
			}

			for (int i = 0; i < entries.size(); ++i) {
				BlockEntry<K, V> e = entries.get(i);
				showTabs(n);
				if (e.left != null) {

					System.err.println("block right of #" + i);
					e.left.show(n + 1);
				} else {
					System.err.println("No block right of #" + i);
				}
			}
			showTabs(n);
			System.err.println("End of Block Info\n\n");
		}

		private void showTabs(int n) {
			// TODO Auto-generated method stub
			for (int i = 0; i < n; ++i) {
				System.err.print(" ");
			}
		}

	}

	@Override
	public SortedMap<K, V> subMap(K fromKey, K toKey) {
		TreeMap<K, V> map = new TreeMap<K, V>();
		root.getRange(map, fromKey, toKey);
		return map;
	}

	@Override
	public SortedMap<K, V> headMap(K toKey) {
		// TODO Auto-generated method stub
		return subMap(root.headKey(), toKey);
	};

	@Override
	public SortedMap<K, V> tailMap(K fromKey) {
		// TODO Auto-generated method stub
		return subMap(fromKey, root.tailKey());
	}

	@Override
	public K firstKey() {
		// TODO Auto-generated method stub
		return root.headKey();
	}

	@Override
	public K lastKey() {
		// TODO Auto-generated method stub
		return root.tailKey();
	}

	@Override
	public int size() {
		// TODO Auto-generated method stub
		return 0;
	}

	@Override
	public boolean isEmpty() {
		// TODO Auto-generated method stub
		return false;
	}

	@Override
	public boolean containsKey(Object key) {
		// TODO Auto-generated method stub
		return get(key) != null;
	}

	@Override
	public boolean containsValue(Object value) {
		// TODO Auto-generated method stub
		return false;
	}

	@Override
	public V get(Object key) {
		// TODO Auto-generated method stub
		return root.get((K) key);
	}

	@Override
	public V put(K key, V value) {
		resultAndSplit<K, V> b = root.put(key, value);
		if (b.splitNode != null) {
			root = new BTBlock<K, V>(root.maxSz, root.comparator);
			root.rightBlock = b.splitNode.right;
			root.entries.add(b.splitNode.entry);
		}
		return b.v;
	}

	@Override
	public V remove(Object key) {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public void putAll(Map<? extends K, ? extends V> m) {
		// TODO Auto-generated method stub

	}

	@Override
	public void clear() {
		// TODO Auto-generated method stub

	}

	@Override
	public Set<K> keySet() {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public Collection<V> values() {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public Set<java.util.Map.Entry<K, V>> entrySet() {
		// TODO Auto-generated method stub
		return null;
	}

}

package btreemap;

import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;

public class TestBtree {

	private static final int N = 50000;

	public static void main(String[] args) {
		BTreeMap<Integer, Integer> map = new BTreeMap<Integer , Integer>();
		Random r = new Random();
		
		ArrayList<Integer> t = new ArrayList<Integer>();
		
		Comparator<Integer> comparator = new Comparator<Integer>() {

			@Override
			public int compare(Integer o1, Integer o2) {
				// TODO Auto-generated method stub
				return o1.intValue() - o2.intValue();
			}
			
		};
		map.setComparator(comparator);
		List<Integer> testVals = new ArrayList<Integer>();
		for (int i =0 ; i < N ; ++i) {
			testVals.add(i);
		}
		for (int i = 0; i < N; ++i ) {
			int x = r.nextInt(testVals.size());
			 x = testVals.remove(x);
			//int x=i;
			t.add(x);
			map.put(x, x);
		}
		
		System.err.println("output " + N + " vals");
		
		map.root.show(0);
		
		for (int i = 0; i < N; ++i) {
			int x = t.get(i);
			
			if ( x != map.get(x)) 
				System.err.println("Expecting " + x + " got " + map.get(x));
			
			
		}
		System.err.println("Checked " + N + " entries");
	}
}

A B+ tree java example

Experiments include timing the run ( e.g. time java -cp . btreemap.BPlusTreeTest1 ) , using an external blocksize + 1 sized leaf block size, so that this is basically the underlying entries TreeMap only , vs , say, 400 internal node size, and 200 external node size . Other experiments include using a SkipListMap instead of a TreeMap.

package btreemap;

import java.util.Collection;
import java.util.Comparator;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.SortedSet;
import java.util.TreeMap;
import java.util.TreeSet;
/**
 * a B+ tree, where leaf blocks contain key-value pairs and 
 * internal blocks have keyed entries pointing to other internal blocks
 * or leaf blocks whose keys are greater than or equal to the associated key.
 * 
 * @author syan
 *
 * @param <K> key type implements Comparable
 * @param <V> value type
 */
public class BPlusTreeMap<K, V> implements SortedMap<K, V> {

	private int maxInternalBlockSize;
	BPlusAnyBlock<K, V> root;
	private int maxExternalSize;

	BPlusTreeMap(int maxInternalSize, int maxExternalSize) {
		this.maxInternalBlockSize = maxInternalSize;
		this.maxExternalSize = maxExternalSize;

	}

	static class SplitOrValue<K, V> {
		V v;
		K k;
		BPlusAnyBlock<K, V> left, right;
		boolean split;

		public boolean isSplit() {
			return split;
		}

		public void setSplit(boolean split) {
			this.split = split;
		}

		public SplitOrValue(V value) {
			v = value;
			setSplit(false);
		}

		public SplitOrValue(BPlusAnyBlock<K, V> left2,
				BPlusAnyBlock<K, V> bPlusBlock) {
			left = left2;
			right = bPlusBlock;
			k = right.firstKey();
			setSplit(true);
			// System.err.printf("\n\n** split occured %s**\n\n", bPlusBlock
			// .getClass().getSimpleName());
		}

	}

	static abstract class BPlusAnyBlock<K, V> {
		public abstract SplitOrValue<K, V> put(K k, V v);

		abstract SplitOrValue<K, V> splitBlock();

		public abstract V get(K k);

		public abstract boolean isEmpty();

		public abstract K firstKey();

	}

	SortedSet<BPlusLeafBlock<K, V>> blockList = getLeafBlockSet();

	SortedSet<BPlusLeafBlock<K, V>> getLeafBlockSet() {
		// return new ConcurrentSkipListSet<BPlusLeafBlock<K, V>>();
		return new TreeSet<BPlusLeafBlock<K, V>>();
	}

	static class BPlusLeafBlock<K, V> extends BPlusAnyBlock<K, V> implements
			Comparable<BPlusLeafBlock<K, V>> {
		SortedMap<K, V> entries = getEntryCollection();

		static <K, V> SortedMap<K, V> getEntryCollection() {
			return new TreeMap<K, V>();
		}

		int maxSize;
		private BPlusTreeMap<K, V> owner;

		public boolean isEmpty() {
			return entries.isEmpty();
		}

		public BPlusLeafBlock(BPlusTreeMap<K, V> bPlusTreeMap,
				SortedMap<K, V> rightEntries) {
			this.owner = bPlusTreeMap;
			maxSize = owner.maxExternalSize;
			entries = rightEntries;
		}

		public SplitOrValue<K, V> put(K k, V v) {
			V v2 = entries.put(k, v);

			if (entries.size() >= maxSize)
				return splitBlock();
			else
				return new SplitOrValue<K, V>(v2);

		}

		public SplitOrValue<K, V> splitBlock() {

			SortedMap<K, V> leftEntries = getEntryCollection();
			SortedMap<K, V> rightEntries = getEntryCollection();

			int i = 0;

			for (Entry<K, V> e : entries.entrySet()) {
				// System.out.println(this.getClass().getSimpleName() +
				// " split entry " + e.getKey());
				if (++i <= maxSize / 2)
					leftEntries.put(e.getKey(), e.getValue());
				else
					rightEntries.put(e.getKey(), e.getValue());
			}
			BPlusLeafBlock<K, V> right = createBlock(rightEntries);
			// System.out.println("finished block split");
			// System.out.println("\nleft block");
			// for (K ik : leftEntries.keySet()) {
			// System.out.print(ik + " ");
			// }
			// System.out.println("\nright block");
			// for (K ik : right.entries.keySet()) {
			// System.out.print(ik + " ");
			// }
			// System.out.println("\n");
			this.entries = leftEntries;

			return new SplitOrValue<K, V>(this, right);
		}

		private BPlusLeafBlock<K, V> createBlock(SortedMap<K, V> rightEntries) {
			return owner.createLeafBlock(rightEntries);
		}

		@Override
		public V get(K k) {
			return entries.get(k);
		}

		@Override
		public int compareTo(BPlusLeafBlock<K, V> o) {

			return ((Comparable<K>) entries.firstKey()).compareTo(o.entries
					.firstKey());
		}

		@Override
		public K firstKey() {
			return entries.firstKey();
		}

	}

	static class BPlusBranchBlock<K, V> extends BPlusAnyBlock<K, V> {
		SortedMap<K, BPlusAnyBlock<K, V>> entries = createInternalBlockEntries();
		int maxSize;

		private BPlusAnyBlock<K, V> left;

		public boolean isEmpty() {
			return entries.isEmpty();
		}

		public BPlusBranchBlock(int maxSize2) {
			this.maxSize = maxSize2;

		}

		public SplitOrValue<K, V> put(K k, V v) {
			BPlusAnyBlock<K, V> b = getBlock(k);

			SplitOrValue<K, V> sv = b.put(k, v);

			if (sv.isSplit()) {

				entries.put(sv.k, sv.right);

				if (entries.size() >= maxSize)
					sv = splitBlock();
				else
					sv = new SplitOrValue<K, V>(null);
			}

			return sv;
		}

		BPlusAnyBlock<K, V> getBlock(K k) {
			assert (entries.size() > 0);
			BPlusAnyBlock<K, V> b = entries.get(k);
			if (b == null) {
				// headMap returns less than k
				SortedMap<K, BPlusAnyBlock<K, V>> head = entries.headMap(k);
				if (head.isEmpty()) {
					b = left;

					// System.out.println("for key " + k
					// + " getting from leftmost block");
					// showEntries();

				} else {
					b = entries.get(head.lastKey());

					// System.out.println("for key " + k
					// + " getting from block with key " + head.lastKey());
					// showEntries();
				}
			}
			assert (b != null);
			return b;
		}

		public void showEntries() {
			System.out.print("entries = ");
			for (K k : entries.keySet()) {
				System.out.print(k + " ");
			}
			System.out.println();
		}

		
		public SplitOrValue<K, V> splitBlock() {

			Set<Entry<K, BPlusAnyBlock<K, V>>> ee = entries.entrySet();
			int i = 0;
			BPlusBranchBlock<K, V> right = new BPlusBranchBlock<K, V>(maxSize);
			SortedMap<K, BPlusAnyBlock<K, V>> leftEntries = createInternalBlockEntries();

			for (Entry<K, BPlusAnyBlock<K, V>> e : ee) {
				// System.out.print("split check " + e.getKey() + ":"
				// );
				if (++i <= maxSize / 2)
					leftEntries.put(e.getKey(), e.getValue());
				else
					right.entries.put(e.getKey(), e.getValue());

			}
			// System.out.println("\n");
			this.entries = leftEntries;

			return new SplitOrValue<K, V>(this, right);
		}

		private SortedMap<K, BPlusAnyBlock<K, V>> createInternalBlockEntries() {
			return new TreeMap<K, BPlusAnyBlock<K, V>>();
		}

		@Override
		public V get(K k) {
			BPlusAnyBlock<K, V> b = getBlock(k);

			return b.get(k);
		}

		@Override
		public K firstKey() {
			return entries.firstKey();
		}

	}

	@Override
	public SortedMap<K, V> subMap(K fromKey, K toKey) {
		TreeMap<K, V> map = new TreeMap<K, V>();
		BPlusLeafBlock<K, V> b1 = getLeafBlock(fromKey);

		BPlusLeafBlock<K, V> b2 = getLeafBlock(toKey);

		SortedSet<BPlusLeafBlock<K, V>> range = blockList.subSet(b1, b2);

		for (BPlusLeafBlock<K, V> b : range) {
			SortedMap<K, V> m = b.entries.subMap(fromKey, toKey);
			map.putAll(m);
		}

		return map;
	}

	private BPlusLeafBlock<K, V> getLeafBlock(K key) {
		BPlusAnyBlock<K, V> b1;
		b1 = root;
		while (b1 instanceof BPlusBranchBlock<?, ?>) {
			b1 = ((BPlusBranchBlock<K, V>) b1).getBlock(key);

		}
		return (BPlusLeafBlock<K, V>) b1;

	}

	public BPlusLeafBlock<K, V> createLeafBlock(SortedMap<K, V> rightEntries) {
		BPlusLeafBlock<K, V> b = new BPlusLeafBlock<K, V>(this, rightEntries);
		blockList.add(b);
		return b;
	}

	@Override
	public SortedMap<K, V> headMap(K toKey) {
		return subMap(firstKey(), toKey);
	};

	@Override
	public SortedMap<K, V> tailMap(K fromKey) {
		return subMap(fromKey, lastKey());
	}

	@Override
	public K firstKey() {
		return blockList.first().entries.firstKey();
	}

	@Override
	public K lastKey() {
		return blockList.last().entries.lastKey();
	}

	@Override
	public int size() {
		return (int) getLongSize();
	}

	private long getLongSize() {
		long i = 0;
		for (BPlusLeafBlock<K, V> b : blockList) {
			i += b.entries.size();
		}
		return i;
	}

	@Override
	public boolean isEmpty() {
		return root.isEmpty();
	}

	@Override
	public boolean containsKey(Object key) {
		return get(key) != null;
	}

	@Override
	public boolean containsValue(Object value) {
		return false;
	}

	@Override
	public V get(Object key) {
		return (V) root.get((K) key);
	}

	@Override
	public V put(K key, V value) {
		if (root == null) {
			SortedMap<K, V> entries = BPlusLeafBlock.getEntryCollection();
			entries.put(key, value);
			root = createLeafBlock(entries);
			return null;
		}
		SplitOrValue<K, V> result = root.put(key, value);
		if (result.isSplit()) {
			BPlusBranchBlock<K, V> root = new BPlusBranchBlock<K, V>(
					maxInternalBlockSize);
			root.left = result.left;
			root.entries.put(result.k, result.right);
			this.root = root;
		}
		return result.v;
	}

	@Override
	public V remove(Object key) {
		return null;
	}

	@Override
	public void putAll(Map<? extends K, ? extends V> m) {
		for (K k : m.keySet()) {
			put(k, m.get(k));
		}
	}

	@Override
	public void clear() {

	}

	@Override
	public Set<K> keySet() {
		TreeSet<K> kk = new TreeSet<K>();
		for (BPlusLeafBlock<K, V> b : blockList) {
			kk.addAll(b.entries.keySet());
		}
		return kk;
	}

	@Override
	public Collection<V> values() {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public Set<java.util.Map.Entry<K, V>> entrySet() {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public Comparator<? super K> comparator() {
		// TODO Auto-generated method stub
		return null;
	}

	public void showLeaves() {

		for (BPlusLeafBlock<K, V> b : blockList) {
			System.out.println("Block");
			for (Entry<K, V> e : b.entries.entrySet()) {
				System.out.print(e.getKey() + ":" + e.getValue() + " ");
			}
			System.out.println();
		}
	}
}

package btreemap;

import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;

/** driver program to test B+ tree */

public class BPlusTreeTest1 {

	private static final int N = 1200000;

	public static void main(String[] args) {
		BPlusTreeMap<Integer, Integer> map = new BPlusTreeMap<Integer, Integer>(
				400, 200 );// 5000002);
		Random r = new Random();

		ArrayList<Integer> t = new ArrayList<Integer>();

		Comparator<Integer> comparator = new Comparator<Integer>() {

			@Override
			public int compare(Integer o1, Integer o2) {
				// TODO Auto-generated method stub
				return o1.intValue() - o2.intValue();
			}

		};

		List<Integer> testVals = new ArrayList<Integer>();
		for (int i = 0; i < N; ++i) {
			testVals.add(i);
		}

		for (int i = 0; i < N; ++i) {
			int x = r.nextInt(N);
			int z = testVals.set(x, testVals.get(0));
			testVals.set(0, z);

		}

		for (int i = 0; i < N; ++i) {
			map.put(testVals.get(i), testVals.get(i));
			showProgress("put", testVals, i);
		}
		System.err.println("output " + N + " vals");

		try {
			for (int i = 0; i < N; ++i) {

				showProgress("get", testVals, i);
				int x = testVals.get(i);
				if (x != map.get(x))
					System.err.println("Expecting " + x + " got " + map.get(x));

			}
			System.err.println("\nChecked " + N + " entries");
		} catch (Exception e) {
			// TODO: handle exception
			e.printStackTrace();
			map.showLeaves();
		}
	}

	private static void showProgress(String label, List<Integer> testVals, int i) {
		if (i % (N / 1000) == 0) {
			System.out.printf("%s %d:%d; ", label, i, testVals.get(i));
			if (i % (N / 10100) == 0)
				System.out.println();
		}
	}
}

Treaps

The invariant in a binary tree is that left is less than right with respect to insertion keys. e.g. for a key with order, ord(L) < ord(R). This doesn't dictate the relationship of nodes however, and left and right rotation does not affect the above. Therefore another order can be imposed. If the order is randomised, it is likely to counteract any skewness of a plain binary tree e.g. when inserting an already sorted input in order.

Below is a java example implementation, including a plain binary tree delete code example.

import java.util.Iterator;
import java.util.LinkedList;
import java.util.Random;

public class Treap1<K extends Comparable<K>, V> {
	public Treap1(boolean test) {
		this.test = test;
	}

	public Treap1() {}
	boolean test = false;
	static Random random = new Random(System.currentTimeMillis());

	class TreapNode {
		int priority = 0;
		K k;
		V val;
		TreapNode left, right;

		public TreapNode() {
			if (!test) {
				priority = random.nextInt();
			}
		}
	}

	TreapNode root = null;

	void insert(K k, V val) {
		root = insert(k, val, root);
	}

	TreapNode insert(K k, V val, TreapNode node) {
		TreapNode node2 = new TreapNode();
		node2.k = k;
		node2.val = val;
		if (node == null) {
			node = node2;
		} else if (k.compareTo(node.k) < 0) {

			node.left = insert(k, val, node.left);

		} else {

			node.right = insert(k, val, node.right);

		}

		if (node.left != null && node.left.priority > node.priority) {
			// left rotate
			TreapNode tmp = node.left;
			node.left = node.left.right;
			tmp.right = node;
			node = tmp;
		} else if (node.right != null && node.right.priority > node.priority) {
			// right rotate
			TreapNode tmp = node.right;
			node.right = node.right.left;
			tmp.left = node;
			node = tmp;
		}
		return node;
	}

	V find(K k) {
		return findNode(k, root);
	}

	private V findNode(K k, Treap1<K, V>.TreapNode node) {
		
		if (node == null)
			return null;
		if (k.compareTo(node.k) < 0) {
			return findNode(k, node.left);
		} else if (k.compareTo(node.k) > 0) {
			return findNode(k, node.right);
		} else {
			return node.val;
		}
	}
	
	static class Deleted {
		boolean success = false;
	}
	
	boolean delete(K k) {
		Deleted del = new Deleted();
		root = deleteNode(k, root, del);
		return del.success;
	}

	private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
		 
		if (node == null) {
			return null;
		} else if (k.compareTo(node.k) < 0) {
			 node.left = deleteNode(k, node.left, del) ;
		} else if (k.compareTo(node.k) > 0) {
			node.right = deleteNode(k, node.right, del);
			
			// k.compareTo(node.k) == 0
		} else if ( node.left == null ) {
				del.success = true;
				return node.right;
		} else if ( node.right == null) {
			  del.success = true;
				return node.left;
		} else if (node.left !=null && node.right != null){
			/*
			// left rotate and all delete on left subtree
			TreapNode tmp = node.right;
			node.right = node.right.left;
		  tmp.left = node;
		  node = tmp;			
			node.left = deleteNode(k , node.left, del);
			*/
			 // more standard method ? doesn't disturb tree structure as much
			// find leftmost descendant of the right child node and replace contents
			TreapNode n2 = node.right;
			TreapNode previous2 = null;
			while (n2.left != null) {
				previous2 = n2;
				n2 = n2.left;
			}
			
			if (previous2 != null) {
				previous2.left = n2.right;
                //n2 has no parent link, orphaned
			} else {
				node.right = n2.right;
                //n2 has no parent link, orphaned
			}

			node.k = n2.k;
			node.val = n2.val;
			del.success = true;
            // once n2 out of scope, the orphaned node at n2 will be garbage collected, 
		}
		
		return node;
	}

	public static void main(String[] args) {
		LinkedList<Integer> dat = new LinkedList<Integer>();

		for (int i = 0; i < 15000; ++i) {
			dat.add(i);
		}
	
			testNumbers(dat, true); // no random priority balancing
			testNumbers(dat, false);
	}

	private static void testNumbers(LinkedList<Integer> dat,
			boolean test) {
		Treap1<Integer, Integer> treap = new Treap1<>(test);

		for (Integer integer : dat) {
			treap.insert(integer, integer);
		}

		long t1 = System.currentTimeMillis();
		Iterator<Integer> desc = dat.iterator();
		int found = 0;
		while (desc.hasNext()) {
			Integer j = desc.next();
			Integer i = treap.find(j);
			if (j.equals(i)) {
				++found;
			}
		}
		long t2 = System.currentTimeMillis();
		System.out.println("found = " + found + " in " + (t2 - t1));
		
		System.out.println("test delete");
		int deleted = 0;
		
		for (Integer integer : dat) {
			if (treap.delete(integer)) 
					++deleted;
		}
		System.out.println("Deleted = " + deleted);
		
	}
}

References

• William Ford and William Tapp. Data Structures with C++ using STL. 2nd ed. Upper Saddle River, NJ: Prentice Hall, 2002.

External links

• Presentation of Iterative Tree Traversals
• Data Structure Trees

Data Structures
Introduction - Asymptotic Notation - Arrays - List Structures & Iterators
Stacks & Queues - Trees - Min & Max Heaps - Graphs
Hash Tables - Sets - Tradeoffs