Piercing Points

Piercing points are nonparallel lines running through and intersecting a plane. They define the place on the plane where a line intersects it.

A) line and plane intersection creates a single point where a line passes through a plane.

Methods to solve:

Edge view method
Cutting plane method

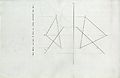
Edge View Method

Using the Edge view method

1) you find a horizontal line in the plane of the front view parallel to the folding line.

2) project the line in the top view. (true length line)

3) find the edge view of the plane by seeing the true length line as a point view. (create a folding line perpendicular to the true length line).

4) the section between the edge view and the given line will be the piercing point. Project the point back to the top and front view.

QUESTION

SOLUTION

Cutting Plane Method

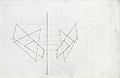
Using the Cutting plane method

1) determine a view and define the cutting plane using points where the line touches the plane

2) project the points into the next view.

3) connect the points to get the trace of the cutting plane.

4) where the trace line intersects the given line is the piercing point of the line through the plane.

QUESTION

SOLUTION

Problem

1) determine lines to use as cutting planes. (two different lines for two different cutting planes)

2) perform the cutting plane method to both lines

3) connect the two piercing points found - this is the line of intersection.

4) determine visibility

Practice by solving the plane and plane intersection problem below.

Problem 1

Solution 1

A dihedral angle is the acute angle formed when two planes intersect.

1) after finding the line of intersection, create an auxiliary view where the line of intersection is in true length.

2) then create another auxiliary view with folding line perpendicular to the true length line.

3) in this view, the true length line will be seen as a point and the two planes as edges

4) measure off the dihedral angle between the edges of both planes.

can be done with rotation to reduce number of auxiliary views needed.

_______________________________________________________________________________________________________________________________________

C) line and solid - When a line intersects a solid, use the line as an edge view of a plane creating a section cut through the solid; use points on the section cut plane to transfer to the view of the solid. Where the points from the cutting plane intersect the line in the other view, you get the piercing points.

Example problem]]

Example problem]]

Piercing Point Problem #1

_________________________________________________________

______________________________________________________________________________

D) plane and solid - Based on the solid you are trying to intersect locate piercing points which lie on an intersecting plane that goes though the solid. This could be based off using the cutting plane method, or with cones and cylinders, determine the piercing points specific to the shape.

_____________________________________________________________________________________________________________________________________

E) solid and solid- when two solids intersect the points of intersecting can be found by first using the piercing points to find where the two faces of the solids meet. (an angular solid requires piercing points at the vertices while rounded solids require multiple arbitrary points around the curve of the solid.

Practice by solving the solid and solid problem below.

Problem 1

Solution 1

_________________________________________________________________________________________________________________________________________

Visibility

Visibility- determining the order from front to back of the solids, lines, or planes.

1)Determine a view after finding the piercing points. (ex. Top view)

2)Project down the piercing points into the other view. (ex. Front view)

3) Determine what geometric object line of projecting intersects first. That is the object that lies on top, (or closest to the figure). in the first view. (ex. top view.)\