Electricity and magnetism/Electrostatics
Electric forces can be produced simply by rubbing different materials together, such as hair on plastic. This creates equal and opposite electric charges on the two surfaces that have been rubbed. We can then observe the attraction of charges of opposite signs, and the repulsion of charges of the same sign:
Coulomb's law
[edit | edit source]Two motionless electric charges exert an electric force on each other proportional to the product of their charges divided by the square of their distance. The two forces, that exerted by A on B and that exerted by B on A, are in the direction of the line which connects the centers of the two charges A and B. These two forces are attractive for charges of opposite signs and repulsive for charges of the same sign.
A field is a physical quantity that can vary at every point in space at every instant. For example, temperature is a field. Coulomb's law says that a motionless electric charge permanently produces an electric force field throughout space:
where is the vector which goes from the charge to the point considered, is its length, is the unit length vector in the direction of and is a constant which depends on the choice of units of measurement.
The force exerted by an electric field on a charge is
So the force exerted by a charge on a charge is
The field is like a mathematical intermediary for calculating the force exerted by one charge on another. But it is much more than a simple mathematical intermediary. It has an autonomous existence. Maxwell showed that light is an electromagnetic wave, that is to say a movement of propagation of the electromagnetic field (, ) of which the electric field is a component.
The electric field on the surface of a positively charged sphere:
The force exerted by two charges on a third is the sum of the forces exerted separately by each of them. All the charges in the Universe produce together throughout space an electric field which is the sum of the fields produced separately by each of them.
The Coulomb force is mathematically similar to the gravitational force: two masses exert a gravitational force on each other proportional to the product of their masses divided by the square of their distance. But the gravitational force is always attractive, because there is no negative mass. On Earth, the weight of a body is the gravitational force that the Earth exerts on it.
According to the theory of relativity, there is no instantaneous interaction at a distance. A charge cannot therefore instantly exert the Coulomb force on another. The force propagation time must be taken into account. This is why Coulomb's law is only a law of electrostatics. It allows the forces between motionless charges to be correctly calculated.
The cohesion of matter is electrostatic
[edit | edit source]A tiny grain of salt
Each line represents a bond between two ions in a NaCl crystal (sodium chloride is common salt). The blue and green colors represent the two ion species. It is a centered cubic crystal. Each Na+ ion is surrounded by 8 close neighbors Cl-. Likewise, each Cl- ion is surrounded by 8 close neighbors Na+. Two nearby ions always have opposite charges, because opposite charges attract each other while charges of the same sign repel each other.
The force that explains the cohesion of solids, atoms and molecules is the Coulomb force. The cohesion of liquids is also caused in part by this electrostatic force, but because the atoms or molecules are in motion, electrodynamic forces can also come into play.
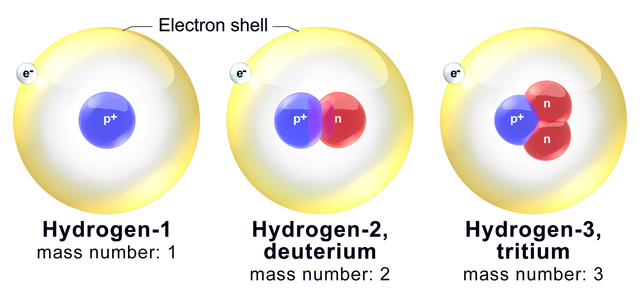
A hydrogen atom consists of one proton, zero, one or two neutrons, and one electron. A proton is a positive charge. An electron is a negative charge, equal but opposite. A neutron is neutral. The electron is linked to the proton by the Coulomb electric force. More generally, an atom consists of a nucleus surrounded by electrons. The charge of the nucleus is positive, equal but opposite to the total charge of the electrons.
When the hydrogen atom is in its ground state, the lowest energy state, the presence of the electron around a proton resembles a spherical cloud:
The proton is at the center. The cloud around represents the presence of the electron.
If the atom is excited, the presence of the electron can have various forms:
A molecule is an assembly of atoms. Electrons are like glue that binds nuclei together. Two positive charges repel each other, but two positive charges separated by a negative charge can attract each other.
An ion is an atom or molecule that has lost or gained one or more electrons. Since atoms and molecules are always electrically neutral, ions are always charged. An atom or molecule that has gained one or more electrons is a negative ion. An atom or molecule that has lost one or more electrons is a positive ion.
A solid is an assembly of atoms, molecules or ions, linked to each other by electrostatic force.
To break an ionic crystal, one must separate ions attracted by electric force:
The attractive forces between charges of opposite signs are greater than the repulsive forces between charges of the same sign. This difference makes all the materials cohesive.
The mass of the nuclei is approximately 5000 times greater than the mass of the electrons accompanying them, because the mass of a proton or neutron is approximately 2000 times that of an electron, and an atom always has the same number of protons and electrons, and a number of neutrons approximately equal to or a little greater than the number of protons (except ordinary hydrogen, which has no neutrons). Since almost all mass is carried by nuclei (made of protons and neutrons), it is more natural to say that electrons are a glue that binds nuclei than to say that nuclei are a glue that binds electrons.
Two point charges of opposite signs should attract each other until they come together. We can calculate that the energy it could provide by falling on each other in this way is infinite. But matter doesn't usually collapse on itself, and it never releases an infinite amount of energy. Bodies always have a lower energy state, which is their ground state. In this state, they cannot give up energy, because they have no lower energy state to go to. Atoms, molecules and ions are in their ground state or in excited states which have higher energy. The hotter a gas is, the more excited its atoms or molecules are. A solid is in an excited state unless its absolute temperature is zero Kelvin.
To explain why an electron from a hydrogen atom does not fall on the proton, or more generally why materials do not collapse on themselves, Coulomb's law is not enough, we need quantum physics.
What is electric voltage?
[edit | edit source]In steady state, the electric voltage is the difference in electric potential between two points. Its unit of measurement is the Volt (V).
What is potential?
To understand potential, we must understand the work of a force.
We can reason about the electric potential in the same way as about the gravitational potential.
We can move a heavy object effortlessly on an ice rink, because we don't have to fight against the force of gravity. On the other hand, it takes a lot of effort to lift a heavy object vertically, because we have to oppose the force of gravity. In the first case, the force of gravity does not work, because the movement is horizontal. In the second case, the force of gravity works, because the movement is vertical.
The work W of a force f on a mobile moving in a straight line over a length d is equal to the scalar product of the force vector f and the displacement vector d:
W = f.d = f d cos
where is the angle between the force vector f and the displacement vector d. f and d are the lengths of the vectors f and d.
The force of gravity is vertical. It does not work for a horizontal displacement because cos 90° = 0. The work of the force of gravity on a mass that is raised from a height is
The work of a force is energy. If > 90°, cos < 0 and W < 0. The work of the force has a negative value because it is the energy lost by a body that moves against the force. This lost energy can be the kinetic energy E = 1/2 mv2. The speed v decreases because the body is slowed down by the force. If < 90°, cos > 0 and W > 0. The work of the force has a positive value because it is the energy acquired by a body that moves by being pushed and accelerated by the force.
In the international system of units of measurement (MKSA, meter, kilogram, second, Ampere), the unit of energy is the Joule (J). One Joule is the work required to move a body one meter against a force of one Newton (N).
1 J = 1 N. 1 m = 1 N.m
The force of gravity on the surface of the Earth is approximately equal to 9.8 N, almost 10 N. One Joule is therefore approximately the energy required to lift a 1 kg body ten centimeters.
When the trajectory of a mobile is a curved line, we calculate the work of a force by reasoning on broken lines which follow the curved trajectory. If the lengths of the segments are shorter and shorter, a broken line becomes more and more similar to the curved line it follows. We find the work of the force by taking the limit of the sum of the work on each segment, when the length of the segments tends to zero. The work of the force is the integral of the scalar product of the force and the displacement vector on the path followed.
By definition of the scalar product, the work of the force of gravity g on an inclined segment AB is equal to g(hA - hB) where hA - hB is the altitude difference between its two ends. Now the altitude difference between A and C is equal to the sum of the altitude differences between A and B and between B and C:
hA - hC = (hA - hB) + (hB - hC)
So the work of the force of gravity g on any path going from A to Z is always equal to g(hA - hZ). It only depends on the difference in altitude of the ends A and Z, not on the path which connects A to Z. We have thus proven in the particular case of the gravity field on the surface of the Earth:
Theorem: the work of the gravitational force does not depend on the path followed.
If we neglect friction, the kinetic energy of a mobile on a roller coaster is the work of the gravitational force from initial rest. It only depends on the height difference , not on the path followed:
The work of a force can depend on the path followed. For example, the work of a friction force is greater as the path followed is longer.
When a force field is such that the work of the force between two points does not depend on the path followed, we can introduce a potential. It is defined by choosing a point of zero potential. The potential at each point in space is then defined by the work of the force on a standard body between this point and the point of zero potential. For the force of gravity, we take as a standard a body whose mass is equal to one. For electric force, the standard is a body whose electric charge is equal to one. The potential is well defined because the work of the force does not depend on the path followed.
Let WXY be the work of the force on a unit body moved from X to Y, VX the potential at point X and O a point of zero potential. By definition of V, VA = WAO and VB = WBO. So VA - VB = WAO - WBO. Or WAO = WAB + WBO. So VA - VB = WAB. The potential difference between two points is therefore always equal to the work of the force on a unit body displaced between these two points.
The electric voltage between two points is the work of the electric force on a unit of charge moved between these two points. In steady state, the work of the electric force does not depend on the path followed, this force therefore derives from a potential. The electric voltage is then a potential difference. It is for the electric force what the difference in altitude is for gravity.
The unit of electric charge is the Coulomb. One Volt (V) is one Joule (J) per Coulomb (C). This is the potential difference necessary to give a charge of one Coulomb an energy of one Joule.
1 V = 1 J/C
When an electric voltage is imposed across a metal wire, an electric current passes through the wire, which is a current of electrons. The electrons are accelerated by the electric force, but their average kinetic energy does not increase, because they are slowed down by the metal. They lose by heating the metal all the energy they gained, through the Joule effect. Electric light was invented by heating a metal wire carrying an electric current to white heat. The electrical resistance of a material measures its ability to slow down electrons or ions passing through it.
Potential energy
[edit | edit source]The gravitational potential energy of a body of mass located at the point is equal to where > is the gravitational potential at point . When a body is at rest, its energy is not visible, not actual, because its kinetic energy is zero. When a body at rest is released into free fall, its gravitational potential energy is transformed into kinetic energy. The energy was already present when the body was at rest, but it had not manifested itself, it was only potential. Its transformation into kinetic energy is an actualization of the potential.
For a body in free fall, released at rest, its kinetic energy at the end of the movement is the actualization of its gravitational potential energy, initially invisible. It is equal to the work of the force of gravity. So the work of force is the actualization of potential. Potential energy is the potential to cause a force to work. We have potential when we have a force that we can put to work.
Energy has many forms: kinetic energy is the energy of a mass due to its speed . Heat is the kinetic energy of atoms and molecules. Gravity energy, electrical energy, and nuclear energy are potential energies that depend on gravitational, electrical, and nuclear forces, respectively. Chemical energy is the electrical energy of atoms and molecules. Light energy is the kinetic energy of photons, the particles of light.
The equation for kinetic energy is only a first approximation. A relativistic calculation, in accordance with Einstein's theory, gives a more precise result.
The transformation of gravitational potential energy into kinetic energy is an example of conservation of energy. The energy never disappears. When a body loses energy, it always gives it to another body, or it transforms it into another form of energy. A hydroelectric dam transforms the energy of gravity into electrical energy. An electric oven converts electrical energy into heat. A nuclear power plant converts nuclear energy into heat and heat into electrical energy. The same goes for all forms of energy production or consumption. The total amount of energy in the Universe is constant.
The potential energy of the mass: E = mc²
[edit | edit source]Even mass is potential energy.
The mass of any body is proportional to the energy that could be released if it were annihilated:
or
where is the speed of light.
A mass always has the potential to be annihilated.
The equation , discovered by Einstein in 1905, can be proven from the fundamental equations of electromagnetism, Maxwell's equations, discovered in 1865. It is explained and proven in the last chapter of this book.
The gradient of a potential
[edit | edit source]When the work of a force does not depend on the path followed, we say that the force field derives from a potential, because we can calculate the force from the potential by taking its gradient.
To understand the concept of gradient, the simplest way is to think about the relief of a mountain. The height h(x,y) of a point on the mountain surface above a point (x,y) in a plane at sea level is a scalar field. We can call it an altitude field. From this scalar field we can define a vector field. For each point (x,y) we define a vector v(x,y) whose direction is the line of greatest slope of the mountain at this point, which is directed upwards and whose length is the slope of the line of greatest slope (if we rise 10 m when we move horizontally 100 m, the slope is equal to 10% = 10/100 = 0.1). The field of the vectors thus defined is the gradient of the altitude field: v = grad h
In these images a scalar field is represented by shades of gray. Its gradient is represented by the arrows. If the scalar field represents the altitude of a relief, the first represents a cone, the second, an inclined plane.
Level lines are lines of equal altitude. If h were a potential, we would call them equipotential lines.
The lines of greatest slope are the lines that always follow the greatest slope. They are always tangent to the vector field at each point. If h were a potential, we would call them field lines.
The lines of greatest slope are always perpendicular to the level lines. Likewise, the field lines are always perpendicular to the equipotential lines.
The black lines are field lines, and the brown lines are the equipotential lines of the electric field created by two equal and opposite charges.
On a terrain map, adjacent contour lines always indicate the same difference in altitude. They are tighter as the slope is greater. If in the same way we draw adjacent equipotential lines for the same potential difference, the lines are tighter as the field is larger.
For a scalar field in a two-dimensional space, we calculate its gradient by taking its two partial derivatives. grad has components and .
The gradient grad of a scalar field in three-dimensional space is the field of vectors whose components are , and .
By definition of the potential, if we move a standard body by the distance dx, its potential variation is dV = -fx dx, where fx is the component of the force f in the x direction. So fx = . Similarly, fy = and fz = - .
The force f on a standard body is the opposite of the gradient of the potential :
f = -grad
This is the general formula that allows us to calculate a force field from a potential.
The Coulomb potential produced by a charge
[edit | edit source]According to Coulomb's law, the electric field E created by a negative charge -q is the field of vectors directed towards the center of the charge whose magnitude is q/r2 where r is the distance from this center. For a positive charge q, it is the same field, except that the vectors are in opposite directions.
The electric field E created by an electric charge q derives from the coulomb potential V = q/r where r is the distance from the center of the charge:
E = -grad V = -grad q/r
The equipotential surfaces are the spheres centered on the charge. Field lines are all straight lines that extend from the center of the charge.
This potential in a plane which passes through the charge can be represented by an altitude field:
Lines of equal altitude are equipotential lines. They are the intersections of the equipotential spheres with a plane which passes through the electric charge.
-dV/dr = q/r2 = E, the length of the vector E if q is a positive charge.
The Coulomb potential of an electric charge is similar to the gravitational potential of a mass:
The lines are the field lines of the gravitational field produced by the Earth, the gravity field.
The potential produced by several charges
[edit | edit source]The electric field created by several charges is the sum of the fields created by each of them separately. Now the gradient of a sum is the sum of gradients, because d(f+g)/dx = df/dx + dg/dx. The electric field created by several charges therefore derives from the sum of the electric potentials created by each of them separately. We thus prove that the electric field created by several charges also derives from a potential. Since Newton's potential is mathematically similar to Coulomb's potential, the same is true for the gravitational force.
The field producing two equal and opposite charges can be represented with field lines:
with equipotential lines:
or by representing its potential as a relief:
We can also see the field lines in space:
The gravitational potential produced by the Earth and the Moon is identical to the electric potential produced by two negative electric charges which would have electric charges proportional to the masses of the Earth and the Moon:
The field lines are in blue, the equipotential lines in red.
We can also represent this potential by an altitude field:
The charge of a capacitor
[edit | edit source]A capacitor is made up of two conductive plates, very close to each other, and separated by an insulating material. Each of the terminals is connected to one of the plates. When the capacitor is turned on, one plate loses some of its electrons and becomes positively charged, while the other plate gains electrons and becomes negatively charged.
We prove with Gauss' theorem (in the chapter on Maxwell's equations) that the electric force field produced by an infinite charged plane, whose charge density is uniform and equal to , is also uniform on each side of the charged plane, perpendicular to it, that its magnitude is , if it is surrounded by emptiness, and its direction on each side of the plane is opposed to its direction on the other side.
Since the electric field produced by several charges is the sum of the fields produced by each of them, the electric field produced by two parallel charged planes, whose surface charge densities are equal and opposite, is therefore uniform between the planes, perpendicular to them, and its greatness is
where is the absolute value of the surface charge density,
while it is equal to zero in all the space exterior to the two charged planes.
The field produced by a finite surface capacitor is identical to the previous one except at the edges:
The work of the electric force on a unit charge between the plates is equal to where is their distance. This remains true for finished plates far from their edges. The voltage between the plates is therefore proportional to their electric charge . The electric charge is therefore proportional to the voltage:
where is the capacitance of the capacitor. measures the amount of charge received by one of the plates for a given voltage.
for plates of surface separated by vacuum, separated by a distance .
Proof:
This is why we make capacitors with large surfaces wound on themselves, separated by an insulating film as thin as possible.
is the vacuum permittivity.
If the plates are separated by an insulating material of permittivity , the capacitance of the capacitor is
Electrostatics of conductive materials
[edit | edit source]A material is conductive when it contains electrical charges that are free to move. In metals, these charges are the conduction electrons. In semiconductors, they can also be holes, absences of electrons that move in a sea of electrons. In ionic solutions like salt water, the mobile electrical charges are positive and negative ions.
Inside a conducting material, the electrostatic field is always zero.
Proof: if the field was not zero, the moving charges would be subject to electric forces which would move them, and the field would not be static.
On the other hand, electric charges can accumulate on the surface of conductive materials. If we place a metallic object near electric charges, its conduction electrons move to exactly compensate for the electric field imposed from the outside to the inside of the metal. The sum of the two fields, the one imposed from the outside and the one imposed by the electrons which have accumulated on the surface, is always equal to zero inside the metal:
On the outer side of the surface of a conductive material, the electric field is perpendicular to the surface.
Proof: if the component of the electric field parallel to the surface was not zero, the surface charges would move to cancel it.
If the surface charge density is positive, the surface electric field is directed outward from the conductive material. If it is negative, it is directed inward.
Proof: if it were the opposite, the electrical forces would push the mobile charges inside the material.
The electric field exerts a force on the surface electric charges but cannot move them, because they cannot move out of the material.
On the surface of a conductive material, the electric field is
where is the surface charge density.
The proof is given from Gauss' theorem, in the chapter on Maxwell's equations.
Electric charges always move in a direction that tends to cancel out the cause of their movement. Two equal and opposite electric charges produce exactly zero electric field if they are exactly superimposed. When they attract each other, they move in a direction which tends to cancel the electric field which is the cause of their movement.
When the terminals of a capacitor are connected with a metal wire, the conduction electrons are subjected to electrical forces, imposed by the charges on the capacitor plates, which move them in the direction of discharge, not in the direction of an increase in charge.
Electrical polarization
[edit | edit source]A body is electrically polarized when a charge difference appears between two of its points.
Conductive bodies are polarized when they are placed in a uniform external electric field. Opposite surface electric charges appear on two opposite sides of the object.
Insulating bodies are also polarized by a uniform electric field. Surface electric charges appear on two opposite sides. How is this possible, when by definition, an insulating body has no free electric charges to move?
In an insulating body, the electrons are attached to the nuclei. There is no free conduction electron to pass from one nucleus to another. Around the nucleus to which they are attached, the electrons have retained a little mobility. They can concentrate on one side or the other in order to compensate for the external electrical force to which they are subjected. We can think of electrons trapped in an atom or molecule as an electric fluid which is retained by the nuclei and which can be deformed. This is why insulating bodies can be polarized by an electric field like conducting bodies.
Inside an insulating body, electric charges are displaced uniformly when it is polarized by a uniform external field. The charge density therefore remains zero inside the material. The surface charge density is the only one that varies.
The movement of positive and negative charges inside an insulating body at the moment of its polarization is a transient electric current. But a permanent electric current cannot flow through an insulating material.
When a body is electrically polarized, it orients itself in the direction of the applied electrical forces:
The potential energy of a system of electric charges
[edit | edit source]How to calculate the electric potential energy of a system of charges?
A charge placed in an electric potential has an electric potential energy .
If we add up the electric potential energies of all the charges with the formula , we do not find the right result. Why ?
To calculate the potential energy of a system, we must calculate the energy spent or received when it is assembled. When we assemble electric charges, the electric field they must pass through is not the same at the beginning and at the end of the assembly. The potential that we calculate when the system is assembled is not the potential of the field that the charges encountered when they were assembled, it is only the potential of the field that a new charge would encounter if brought near the system.
The first of the assembled charges does not encounter any electric force field to be put into place, because no charge is present before it. The second charge meets the field produced by the first. The third charge meets the field produced by the first two, and so on until the last charge, which encounters the field produced by all the previous ones.
Example: the potential energy of a charged capacitor
To charge a capacitor, electrons must be moved from one of its plates to the other. The first charge moved encounters no field, because the capacitor is not charged. The work that must be done to move it is therefore . If the capacitor is already charged by a charge , a new charge encounters an electric force field, therefore a potential difference between its starting point and its arrival point . So
is therefore the electric potential energy of a capacitor charged by a charge , where is its capacitance and the potential difference between its plates.
Where is the electric potential energy?
[edit | edit source]Electric potential energy is attributed to electric charges. Is this energy carried by the charges? Is it located on the charges?
. Mass is always energy. Energy always has mass. This equation is proven at the end of this book, where it is shown that light trapped in a box increases the mass of the box. Light therefore has a mass equal to its energy divided by .
If the electric potential energy were localized on the charges, variations in their energy would cause their mass to vary. But this effect has never been observed.
The electric potential energy of a system of charges is in all the space where they produce an electric field, it is carried by the electric field. The volume density of electrical energy in an electrostatic field is
where is the electric potential energy contained in a small volume .
When we bring two electric charges of the same sign together, we increase the energy of the electric field:
If we bring two charges of opposite signs together, we reduce the energy of the electric field. The same is true for the nuclear forces that hold neutrons and protons together in a nucleus. We have to provide them with energy to separate them. This is why their mass is greater when they are separated than when they are united:
It takes infinite energy to separate the three quarks that make a proton, or a neutron. This is why we can never observe an isolated quark.
Let us show that allows us to correctly calculate the electric potential energy of a charged capacitor:
where is the surface area of the capacitor, the distance between the plates, the volume between the plates and the field produced by a surface charge density .
Now
and
so
When we define the potential, we are free to choose a point of zero potential. To calculate electric forces, any choice is suitable because two potentials that differ by a constant have the same gradient. But to calculate the energy and the presence of its mass, we are obviously not free to modify the energy of all the charges by choosing another point of zero potential. The point of zero potential must be chosen in such a way that an electric charge can be placed there without making any effort. This is why when we calculate the electrostatic energy of a system of charges, we assume that they are placed in empty space, and we define a zero potential at infinity. The force exerted by electric charges tends to zero at infinity. There is no effort to be made against their electric force if we are very far from them.
When a dipole moment is created by the separation of equal and opposite charges, as when charging a capacitor, we can reason as if the charge density were initially zero everywhere. So there is no electric force anywhere. Any point can therefore be chosen as a point of zero potential.