Haskell/Solutions/Category theory
Which law implies transitivity?
[edit | edit source]Formally, transitivity of a partial order is defined as: for any , , and if and then . In the category defined by a partial order this translates to: for any objects , , and if there exist morphisms and then there exists a morphism . This is guaranteed by the second law of categories, i.e., that they are closed under composition. Indeed, the last morphism is a composition of the first two.
Why does adding an arrow break category laws?
[edit | edit source]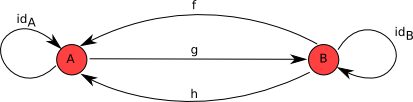
Let's consider what must be the result of the compositions and . Notice that since and then and given that there is only one morphism from to , namely , it follows that . Using similar reasoning we can show that .
Now, let us consider the composition ; substituting into it yields , which can be simplified to using the third law of categories. However, the first law of categories states that this composition should be equal to , yet .























