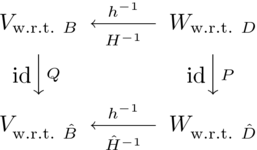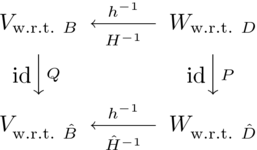- This exercise is recommended for all readers.
- This exercise is recommended for all readers.
- Problem 3
Suppose that, with respect to

the transformation  is represented by
this matrix.
is represented by
this matrix.

Use change of basis matrices to represent  with respect
to each pair.
with respect
to each pair.
-
 ,
,

-
 ,
,

- Answer
Recall the diagram
and the formula.
|
|
| 
|
|
| 
|
- These two

show that

and similarly these two

give the other nonsingular matrix.

Then the answer is this.

Although not strictly necessary, a check is reassuring.
Arbitrarily fixing

we have that

and so  is this.
is this.

Doing the calculation with respect to  starts with
starts with

and then checks that this is the same result.

- These two

show that

and these two

show this.

With those, the conversion goes in this way.

As in the prior item, a check provides some confidence that this
calculation was performed without mistakes.
We can for instance, fix the vector

(this is selected for no reason, out of thin air).
Now we have

and so  is this vector.
is this vector.

With respect to  we first calculate
we first calculate

and, sure enough, that is the same result for  .
.

- This exercise is recommended for all readers.
- This exercise is recommended for all readers.
- Problem 5
Use Theorem 2.6 to show that a square matrix is nonsingular if and only if it is equivalent to an identity matrix.
- Answer
Any  matrix is nonsingular if and only if it has
rank
matrix is nonsingular if and only if it has
rank  , that is, by Theorem 2.6,
if and only if it is matrix equivalent to
the
, that is, by Theorem 2.6,
if and only if it is matrix equivalent to
the  matrix whose diagonal is all ones.
matrix whose diagonal is all ones.
- This exercise is recommended for all readers.
- This exercise is recommended for all readers.
- Problem 8
Must matrix equivalent matrices have matrix equivalent transposes?
- Answer
Yes. Row rank equals column rank, so the rank of the transpose equals the rank of the matrix. Same-sized matrices with equal ranks are matrix equivalent.
- Problem 9
What happens in Theorem 2.6 if  ?
?
- Answer
Only a zero matrix has rank zero.
- This exercise is recommended for all readers.
- This exercise is recommended for all readers.
- Problem 11
Show that a zero matrix is alone in its matrix equivalence
class.
Are there other matrices like that?
- Answer
By Theorem 2.6, a zero matrix is alone in its class because it is the only  of rank zero. No other matrix is alone in its class; any nonzero scalar product of a matrix has the same rank as that matrix.
of rank zero. No other matrix is alone in its class; any nonzero scalar product of a matrix has the same rank as that matrix.
- Problem 14
Are matrix equivalence classes closed under scalar
multiplication?
Addition?
- Answer
They are closed under nonzero scalar multiplication, since a nonzero scalar multiple of a matrix has the same rank as does the matrix. They are not closed under addition, for instance,  has rank zero.
has rank zero.
- Problem 15
Let  represented by
represented by
 with respect to
with respect to  .
.
- Find
 in this specific case.
in this specific case.

- Describe
 in the general case where
in the general case where
 .
.
- Answer
- We have

and thus the answer is this.

As a quick check, we can take a vector at random

giving

while the calculation with respect to 

yields the same result.

- We have
|
|
| 
|
|
| 
|
and, as in the first item of this question

so, writing  for the matrix whose columns are the basis vectors,
we have that
for the matrix whose columns are the basis vectors,
we have that  .
.
- Problem 16
- Let
 have bases
have bases  and
and  and
suppose that
and
suppose that  has the basis
has the basis  .
Where
.
Where  , find the formula that computes
, find the formula that computes
 from
from  .
.
- Repeat the prior question with one basis
for
 and two bases for
and two bases for  .
.
- Answer
- The adapted form of the arrow diagram is this.

Since there is no need to change bases in
 (or we can
say that the change of basis matrix
(or we can
say that the change of basis matrix  is the identity), we have
is the identity), we have
 where
where
 .
.
- Here, this is the arrow diagram.

We have that  where
where
 .
.
- Problem 17
- If two matrices are matrix-equivalent and invertible,
must their
inverses be matrix-equivalent?
- If two matrices have matrix-equivalent inverses, must the two
be matrix-equivalent?
- If two matrices are square and matrix-equivalent, must their
squares be matrix-equivalent?
- If two matrices are square and have matrix-equivalent squares,
must they be matrix-equivalent?
- Answer
- Here is the arrow diagram, and a version of that diagram
for inverse functions.
Yes, the inverses of the matrices represent the
inverses of the maps.
That is, we can move from the lower right to the lower left by
moving up, then left, then down.
In other words, where  (and
(and  invertible)
and
invertible)
and  are invertible then
are invertible then
 .
.
- Yes; this is the prior part repeated in different terms.
- No, we need another assumption: if
 represents
represents
 with respect to the same starting as ending bases
with respect to the same starting as ending bases  ,
for some
,
for some  then
then  represents
represents
 .
As a specific example,
these two matrices are both rank one and so they are
matrix equivalent
.
As a specific example,
these two matrices are both rank one and so they are
matrix equivalent

but the squares are not matrix equivalent— the square of the
first has rank one while the square of the second has rank zero.
- No.
These two are not matrix equivalent but have matrix equivalent
squares.

- This exercise is recommended for all readers.
- Problem 18
Square matrices are similar if they represent the same
transformation, but each with respect to the same ending as starting
basis.
That is,  is similar to
is similar to  .
.
- Give a definition of matrix similarity like that of
Definition 2.3.
- Prove that similar matrices are matrix equivalent.
- Show that similarity is an equivalence relation.
- Show that if
 is similar to
is similar to  then
then
 is similar to
is similar to  , the cubes are similar, etc.
Contrast with the prior exercise.
, the cubes are similar, etc.
Contrast with the prior exercise.
- Prove that there are matrix equivalent matrices
that are not similar.
- Answer
- The definition is suggested by the appropriate
arrow diagram.

Call matrices  similar if there
is a nonsingular matrix
similar if there
is a nonsingular matrix  such that
such that
 .
.
- Take
 to be
to be  and take
and take  to be
to be  .
.
- This is as in Problem 10.
Reflexivity is obvious:
 .
Symmetry is also easy:
.
Symmetry is also easy:  implies that
implies that
 (multiply the first equation from the right
by
(multiply the first equation from the right
by  and from the left by
and from the left by  ).
For transitivity, assume that
).
For transitivity, assume that  and that
and that
 .
Then
.
Then  and we are finished
on noting that
and we are finished
on noting that  is an invertible matrix with inverse
is an invertible matrix with inverse
 .
.
- Assume that
 .
For the squares:
.
For the squares:
 .
Higher powers follow by induction.
.
Higher powers follow by induction.
- These two are matrix equivalent but their squares are not
matrix equivalent.

By the prior item, matrix similarity and matrix equivalence are thus
different.