In the propositional case we defined the resolution inference rule by
"cutting away" a pair of complementary literals in two clauses which
are resolved upon. In the first order case however this is not always
sufficient:

In these two clauses there are no complementary literals, however,
after substituting the term  for the variable
for the variable  in
in  and
and
 for
for  in
in  we arrive at:
we arrive at:

Now we can apply the inference rule from propositional logic and
arrive at the resolvent  .
.
Another possibility is to substitute  for
for  in
in  to get
to get

and then we can have the resolvent  from
from  and
and  , which is in a certain sense more general then the resolvent derived
previously.
, which is in a certain sense more general then the resolvent derived
previously.
A substitution  is a function, which maps variables
to terms and which is the identical mapping almost everywhere. Hence
it can be represented as
is a function, which maps variables
to terms and which is the identical mapping almost everywhere. Hence
it can be represented as

If  are groundterms, we call
are groundterms, we call  a
ground substitution. The empty substitution is
notated by
a
ground substitution. The empty substitution is
notated by  .
.
Let  be a substitution and
be a substitution and  an
expression (i.e. a literal or a term), then
an
expression (i.e. a literal or a term), then  is the expression,
obtained from
is the expression,
obtained from  by replacing simultaneously each occurrence of
by replacing simultaneously each occurrence of
 in
in  by the term
by the term  .
.
Example:
With  and
and  , we get
, we get 
Let  and
and  be substitutions. Then the composition of substitutions, denoted by
be substitutions. Then the composition of substitutions, denoted by  ,
is the substitution, which is obtained from
,
is the substitution, which is obtained from  by deleting any element
by deleting any element
 for which
for which  and any element
and any element
 such that
such that  .
.
Example:
Let  be a set of expressions and
be a set of expressions and  a
substitution,
a
substitution,  is unifier for
is unifier for  iff
iff

.
A unifier  is called most general unifier iff for every
unifier
is called most general unifier iff for every
unifier  there is a substitution
there is a substitution  such that
such that  .
.
In the following we discuss an algorithm for computing most general
unifiers. For this we assume a set of terms  to be unified. First we transform this into a set of equations
by introducing a new variable not yet occurring in this set, say
to be unified. First we transform this into a set of equations
by introducing a new variable not yet occurring in this set, say  and by defining the set of equations
and by defining the set of equations

We will now transform this set such that its unifiers stay invariant,
where a  is a unifier of a set of
is a unifier of a set of  if
if  holds.
holds.
Unification
Given a set of expression. Transform it into a set of equations  as defined above. Apply the following transformation rules as long as
possible:
as defined above. Apply the following transformation rules as long as
possible:
 Orient
Orient
where  is a variable and
is a variable and  a non-variable term
a non-variable term
 Delete
Delete
 Decompose (Termreduction)
Decompose (Termreduction)
![{\displaystyle {\frac {R\uplus \{x=t\}}{R[x/t]\uplus \{x=t\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b00afc306f39edb6d78dd4dd9cf1882d8d2aed33) Eliminate (Elimination of variable I)
Eliminate (Elimination of variable I)
if  not in
not in  , but in
, but in 
![{\displaystyle {\frac {R\uplus \{x=y\}}{R[x/y]\uplus \{x=y\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3375d2f6a69e886d488026b47fd1c7a5ecf41413) Coalesce (Elimination of variable II)
Coalesce (Elimination of variable II)
if  in
in 
 Conflict
Conflict
if  or
or 
 Occur Check
Occur Check
if  in
in 
Let  be a set of expressions. The above unification algorithm
terminates. If it returns
be a set of expressions. The above unification algorithm
terminates. If it returns  , there is no unifier for
, there is no unifier for  , otherwise
, otherwise
 is transformed into a set of equation
is transformed into a set of equation  , which represents the most general unifier for
, which represents the most general unifier for  .
.
Let two or more literals of a clause  have a unifier
have a unifier  , then
, then
 is called a factor of
is called a factor of  .
.
Example:
With  and
and  we
get the factor
we
get the factor 
Let  and
and  be two clauses with no variables in common, such
that
be two clauses with no variables in common, such
that  and
and  and
and  and
and  have a most
general unifier
have a most
general unifier  . A binary resolvent of
. A binary resolvent of  and
and
 is
is

Example:
Given  and
and  . After
renaming
. After
renaming  into
into  we get the resolvent
we get the resolvent
 by using the most general unifier
by using the most general unifier  .
.
We often depict resolvent graphically, e.g.

A resolvent of two clauses  and
and  is one of the
following binary resolvents:
is one of the
following binary resolvents:
- a binary resolvent of
 and
and 
- a binary resolvent of
 and a factor of
and a factor of 
- a binary resolvent of a factor of
 and
and 
- a binary resolvent of a factor of
 and a factor of
and a factor of 
Example:
Given  and
and  .
.
A factor of  is
is  . A binary
resolvent of
. A binary
resolvent of  and
and  and hence also of
and hence also of  and
and
 is
is  .
.
The following lemma is used in the completeness proof of resolution.
If  and
and  are instances of
are instances of  and
and  ,
respectively, and
,
respectively, and  is a resolvent of
is a resolvent of  and
and  ,
then there is a resolvent
,
then there is a resolvent  of
of  and
and  such that
such that
 is an instance of
is an instance of  .
.
 Figure 1
Figure 1
A set  of clauses is unsatisfiable iff the empty clause can be
derived from
of clauses is unsatisfiable iff the empty clause can be
derived from  by resolution.
by resolution.
Proof:
Assume that  is unsatisfiable. Let
is unsatisfiable. Let  be
the ground atom set of
be
the ground atom set of  , hence the Herbrand basis. Let
, hence the Herbrand basis. Let  be a
complete binary tree, as given in Figure 2. According to Herbrand's theorem
(version1) there exists a closed finite semantic tree
be a
complete binary tree, as given in Figure 2. According to Herbrand's theorem
(version1) there exists a closed finite semantic tree
 . There are two cases:
. There are two cases:
- If
 consists only of one node (hence the root), The interpretation to be collected from the empty branch in this tree falsifies only the empty clause. Hence the empty clause must be in
consists only of one node (hence the root), The interpretation to be collected from the empty branch in this tree falsifies only the empty clause. Hence the empty clause must be in  .
.
- Assume
 consists of more than one node. Then there must be an inference node
consists of more than one node. Then there must be an inference node  in
in  , hence both its descendants
, hence both its descendants  and
and  are failure nodes. If such a node would not exist, every node would have at least one non-failure node, which would mean that there is at least an infinite path in
are failure nodes. If such a node would not exist, every node would have at least one non-failure node, which would mean that there is at least an infinite path in  , which would violate, that fact that it is a finite closed semantic tree. Let
, which would violate, that fact that it is a finite closed semantic tree. Let  given as described above; and let
given as described above; and let 
Now, let  and
and  be ground instances of clauses
be ground instances of clauses  and
and  , such that
, such that  is falsified by
is falsified by  and
and  by
by  , such that both are not falsified by
, such that both are not falsified by  .
.
Hence we have  and
and  and we can construct the resolvent
and we can construct the resolvent

 must be false in
must be false in  , because both
, because both  and
and  are false in
are false in  . According to the Lifting Lemma 5 there exists a resolvent
. According to the Lifting Lemma 5 there exists a resolvent  of
of  and
and  , such that
, such that  is a ground instance of
is a ground instance of  . Let
. Let  be the closed semantic tree for
be the closed semantic tree for  , obtained from
, obtained from  by deleting all nodes below the first node which falsifies
by deleting all nodes below the first node which falsifies  . Note, that
. Note, that  is unsatisfiable if and only if
is unsatisfiable if and only if  is unsatisfiable. Clearly,
is unsatisfiable. Clearly,  has less nodes than
has less nodes than  and we now can iterate this process until only the root of the semantic tree is remaining. This, however is only possible if the empty clause
and we now can iterate this process until only the root of the semantic tree is remaining. This, however is only possible if the empty clause  is derivable.
For the opposite direction, assume that
is derivable.
For the opposite direction, assume that  is derivable by
resolution from
is derivable by
resolution from  and let
and let  the resolvents
constructed during this process. Assume
the resolvents
constructed during this process. Assume  is satisfiable and
is satisfiable and
 to be a model for
to be a model for  . From the correctness lemma according to
the propositional case we known, that if a model satisfies two
clauses it also satisfies its resolvent. Therefore
. From the correctness lemma according to
the propositional case we known, that if a model satisfies two
clauses it also satisfies its resolvent. Therefore  has to satisfy
has to satisfy
 ; this, however, is impossible, because one of this
resolvents is
; this, however, is impossible, because one of this
resolvents is  .
.
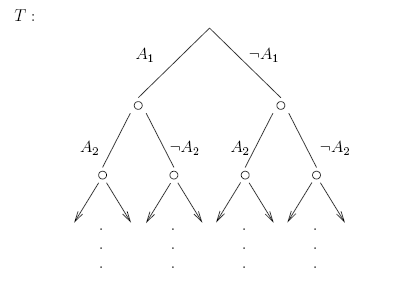
Figure 2
Indicate in each case a derivation of the empty clause with predicate-logical resolution!


(

)


Show the following Lifting lemma by means of
induction over the term- and formula construction:
Is  a predicate-logical formula, and
a predicate-logical formula, and  a fitting interpretation for
a fitting interpretation for
 and
and ![{\displaystyle F[x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f6c858d274f9d292d0d8348142a04658048d3e) . Then
. Then
![{\displaystyle {\mathcal {I}}(F[x/t])={\mathcal {I}}_{[x/{\mathcal {I}}(t)]}(F),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af8c733f03d88cddf67e35e698af3075c6d6415b)
is valid, if  does not contain any variable that
does not contain any variable that ![{\displaystyle [x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff5a99a8641a9e4e67622b7b0e152230a5f72ed1) is laced
is laced
by the substitution in  .
.

Compute - if possible - the most general unifier of following sets of clauses:





Determine all direct resolvents of the following pairs of clauses:
 and
and 
 and
and 
 and
and 
 and
and 

Compute - if possible - the most general unifier of following sets of clauses:





Determine all direct resolvents of the following pairs of clauses:
 and
and 
 and
and 
 and
and 

Give for the following set of clauses (a) a linear derivation,
(b) a derivation with unit resolution, (c) a further (maximally
short) derivation of the empty clause by means of
predicate-logical resolution!


Indicate in each case a derivation of the empty clause with predicate-logical resolution!


(

)




















































![{\displaystyle {\frac {R\uplus \{x=t\}}{R[x/t]\uplus \{x=t\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b00afc306f39edb6d78dd4dd9cf1882d8d2aed33)

![{\displaystyle {\frac {R\uplus \{x=y\}}{R[x/y]\uplus \{x=y\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3375d2f6a69e886d488026b47fd1c7a5ecf41413)





























































![{\displaystyle F[x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f6c858d274f9d292d0d8348142a04658048d3e)
![{\displaystyle {\mathcal {I}}(F[x/t])={\mathcal {I}}_{[x/{\mathcal {I}}(t)]}(F),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af8c733f03d88cddf67e35e698af3075c6d6415b)
![{\displaystyle [x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff5a99a8641a9e4e67622b7b0e152230a5f72ed1)




















