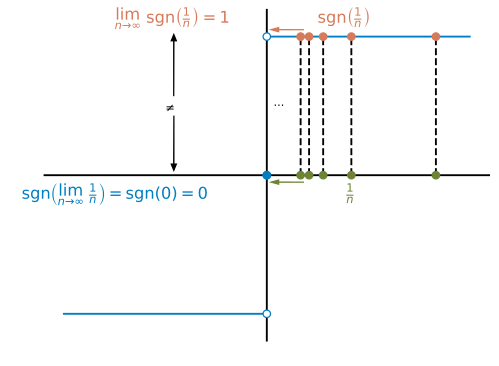Epsilon-delta definition of continuity – "Math for Non-Geeks"

Motivation and derivation

First examples

Consider the limit $\lim _{n\to \infty }\exp \left({\tfrac {1}{n}}\right)$. In school, this limit would be calculated as follows:

${\begin{aligned}\lim _{n\to \infty }\exp \left({\frac {1}{n}}\right)&=\exp \left(\lim _{n\to \infty }{\frac {1}{n}}\right)\\[0.5em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }{\frac {1}{n}}=0\right.}\\[0.5em]&=\exp(0)\\&=1\end{aligned}}$

Intuitively, this calculation makes sense: if ${\tfrac {1}{n}}\to 0$, then $\exp \left({\tfrac {1}{n}}\right)\to \exp(0)$ should hold. But can we really argument like that? Why should we be allowed to "pull" the limit inside the function brackets? Let us consider another example: the sign function $\operatorname {sgn}(x)$, which is returning the sign of $x$:

$\operatorname {sgn}(x)={\begin{cases}1&x>0\\0&x=0\\-1&x<0\end{cases}}$

Since ${\begin{aligned}{\tfrac {1}{n}}>0\end{aligned}}$ there is:

$\lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)=\lim _{n\to \infty }1=1\neq 0=\operatorname {sgn}(0)=\operatorname {sgn} \left(\lim _{n\to \infty }{\frac {1}{n}}\right)$

So $\lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)\neq \operatorname {sgn} \left(\lim _{n\to \infty }{\tfrac {1}{n}}\right)$. This simple example shows that the limit may not simply be pulled into the function brackets. The function plot shows, why this worked with $\exp(x)$, but not with $\operatorname {sgn}(x)$. For $\exp(x)$, the sequence $\left(\exp \left({\tfrac {1}{n}}\right)\right)_{n\in \mathbb {N} }$ converges to $\exp(0)$, when taking the limit $n\to \infty$:

The sign function has a "jump" in the graph at $x=0$ and hence, the sequence $\left(\operatorname {sgn} \left({\tfrac {1}{n}}\right)\right)_{n\in \mathbb {N} }$ does not converge to $\operatorname {sgn}(0)$:

We note: There are certain functions, where the limit may be pulled into the brackets, wile for other functions this may not always work.

Jumps and continuity

The reason why we cannot pull the limit into the sign function $\operatorname {sgn} \left({\tfrac {1}{n}}\right)$, is because its graph has a "jump" at $x=0$. Let us now try to figure out, why pulling the limit into the brackets does not work, if the graph has a jump at the limit of the argument sequence. We assume $f$ to have the following graph:

Graph of a function f with a jump at x0, where the right-handed limit at x0 exists.

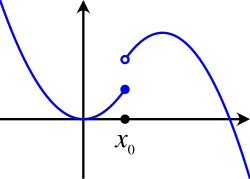
When approaching $x_{0}$ from the left, the function values will also approach $f(x_{0})$. So if the sequence of arguments consists only or almost only (meaning: with finitely many exceptions) of real numbers smaller or equal $x_{0}$, then we may pull the limit inside the brackets. However, this fails if infinitely many elements bigger than $x_{0}$ appear in the sequence of arguments. Their function values will not approach $f(x_{0})$, as the graph is having a jump at $x_{0}$, when looking to the right. This jump causes a minimal distance which function values in the proximity and right of $x_{0}$ cannot fall below. The jump at $x_{0}$ prevents us from being able to pull the limit into the brackets for some sequences of arguments.

The same happens if the graph has a jump at $x_{0}$ in the left-handed direction:

Graph of the function f with a jump at x0, where the left-handed limit at x0 exists.

Here, pulling the limit in fails whenever the sequence of arguments contains infinitely many elements smaller than $x_{0}$. Function values left of $x_{0}$ will not approach $f(x_{0})$ due to the jump.

Mind that the situation may be different if $f$ is not defined at the jump:

Graph of a function f with a jump at x0, where the function is not defined.

Here, the expression $f\left(\lim _{n\to \infty }x_{n}\right)$ does not make sense, since $f$ is not defined at $x_{0}$. So we do not need to consider, whether pulling in the limes is allowed there. For all other real numbers, the graph of $f$ is continuous. We observe: A jump does only cause discontinuity of a function $f$, if $f$ is even defined at the position of the jump.

Transition to a formal definition

Let us take again a function $f$ with a jump at $x_{0}$. When approaching the argument $x_{0}$ from one side, a certain minimal distance between $f(x)$ and $f(x_{0})$ will always be kept. This minimal distance between $f(x)$ and $f(x_{0})$ is caused by the jump at $x_{0}$. When approaching $x_{0}$ from the other side, the $f(x)$-values will come arbitrarily close to $f(x_{0})$ (provided there is no second jump).

For $x$-values that should approach arbitrarily (=„infinitely“) close to $x_{0}$, we can use the notion of a sequence. To do so, we treat the $x$-values as a sequence $(x_{n})_{n\in \mathbb {N} }$, converging to $x_{0}$. The notion of a sequence is useful, as we need usually need infinitely many $x$-values for the approach and sequences are containing infinitely many elements as well.

Now, let us assume that we approach $x_{0}$ from the side, where our $f(x_{n})$ obey a minimal distance to $f(x_{0})$ for $x$ in the vicinity of $x_{0}$. This minimal distance will be sustained in the limit process $\lim _{n\to \infty }$. In case that $\lim _{n\to \infty }f(x_{n})$ exists, we can therefore be sure that $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$.

However, in our example we may also choose the sequence $(x_{n})_{n\in \mathbb {N} }$ such that $\lim _{n\to \infty }f(x_{n})=f(x_{0})$. This will, for instance, be the case when $x_{0}$ is approached by our $x_{n}$ from the other side. So in order to have $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$, we cannot make an arbitrary choice of our sequence converging to $x_{0}$. But we certainly know that there are sequences $(x_{n})_{n\in \mathbb {N} }$, for which $f(x_{n})$ does not tend towards $f(x_{0})$.

Derivation of the sequence criterion

Let us recap what we found so far:

So if there is a jump at $x\in D$ then we may not pull the limit inside the brackets (i.e. $\lim _{n\to \infty }f(x_{n})\neq f(x)=f\left(\lim _{n\to \infty }x_{n}\right)$) for at least one sequence of arguments $(x_{n})_{n\in \mathbb {N} }$ converging to $x$. Now, our intuition tells us that a function is discontinuous at some argument $x$, whenever its graph has a jump there. Therefore, we may define:

In order to find the corresponding definition for continuity at $x$, we just need to take the negation of the above definition for discontinuity. That means, we may understand continuity as absence of a jump, where the exact definition reads:

So we memorize: in case a function is continuous at some argument $x$, we may pull the limit inside the brackets for any sequence of arguments convrging to $x$. This is the sequence criterion of continuity. The entire function $f$ is considered to be continuous, if it is continuous at each argument $x\in D$ in its domain of definition. The definition of continuity for a function $f$ therefore reads:

So let us recap: For continuous functions $f$ , we may always pull the limit inside the brackets – regardless of the limit $x$ of the sequence of arguments. For instance, the exponential function is continuous, so we may always pull the limit inside the brackets of this function. The sign function is discontinuous at $x=0$ , so we may not pull the limit inside the brackets, if the sequence of argument converges to zero.

Formal definition

In the above section, we already learned the definition of continuity. Let us formalize this:

Definition (Sequence criterion of continuity for a single argument)

A function $f:D\to \mathbb {R}$ with $D\subseteq \mathbb {R}$ is continuous at an argument $x_{0}\in D$, if for all squences $(x_{n})_{n\in \mathbb {N} }$ with $\forall n\in \mathbb {N} :x_{n}\in D$ and $\lim _{n\to \infty }x_{n}=x_{0}$ there is:

$\lim _{n\to \infty }f(x_{n})=f\left(\lim _{n\to \infty }x_{n}\right)=f(x_{0})$

A function is said to be continuous if it is continuous at each argument:

Definition (Sequence criterion of continuity)

A function $f:D\to \mathbb {R}$ with $D\subseteq \mathbb {R}$ is continuous, if for all $x\in D$ and all sequences $(x_{n})_{n\in \mathbb {N} }$ with $\forall n\in \mathbb {N} :x_{n}\in D$ and $\lim _{n\to \infty }x_{n}=x$ there is:

$\lim _{n\to \infty }f(x_{n})=f\left(\lim _{n\to \infty }x_{n}\right)=f(x)$

So continuity guarantees us that we are allowed to pull the limit inside the brackets. This may simplify calculations of limits tremendously - and indeed, continuity is a concept one may encounter frequently when calculating limits.

Consequences of this definition

We just found a formal definition of continuity by using our intuition of jumps. This definition turned out to be useful over the years and is therefore accepted in the mathematical community as the definition of continuity. And we will use it for the following considerations as well. So if we want to decide whether a function is continuous, we will replace our first intuition by the sequence criterion which we just found. This will also have some side effects. We consider the topological sine function:

$f:\mathbb {R} \to \mathbb {R} :x\mapsto {\begin{cases}\sin \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}}$

Its graph is given by:

Graph der topologischen Sinusfunktion

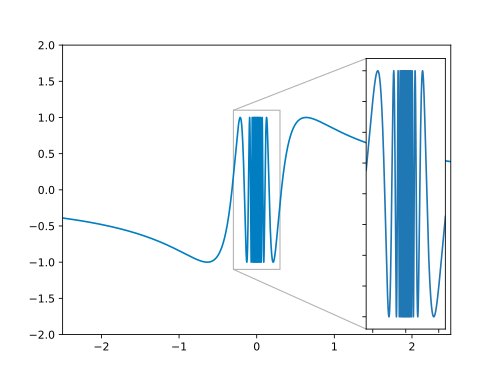
Our first intuition is not suitable for deciding, whether this function is continuous at $x=0$ , since it is oscillating here infinitely many times with the period of oscillation tending to zero. The graph itself does not look as if there would be a jump. However, using the sequence criterion of continuity, we may show that the topological sine function is discontinuous at $x=0$, which corresponds to the infinitely fast oscillations (Exercise).

As a byproduct of our definition, we found a type of discontinuity differing from a jump. It is also called essential discontinuity . And we need to accept these kind of discontinuities, if we want to use the sequence criterion as a definition for discontinuities. Please note that this is one of the standard definitions in mathematics. So denying it or looking for an alternative would certainly make us some lonely outsiders in the world of mathematicians!

Examples for the sequence criterion

Application of the sequence criterion

We have just proven that the quadratic funtion is continuous. So we may pull the limit inside the brackets without further thinking about it. This is a nice thing about continuity, as the following example underlines:

Common sketches of proofs

Proofs of continuity using the sequence criterion

In order to prove continuity of a function at some $x_{0}$ , we need to show that for each sequence $(x_{n})_{n\in \mathbb {N} }$ of arguments converging to $\lim _{n\to \infty }x_{n}=x_{0}$ , there is $\lim _{n\to \infty }f(x_{n})=f(x_{0})$ . A proof for this could schematically look as follows:

In order to prove continuity for the function $f$ (for all arguments in its domain of definition), we need to slightly adjust that scheme:

Proving discontinuity using the sequence criterion

In order to show that a function $f:D\to \mathbb {R}$ is discontinuous at $x_{0}\in D$ using the sequence criterion, we need to find one specific sequence of arguments $(x_{n})_{n\in \mathbb {N} }$ with $x_{n}\in D$ for all $n\in \mathbb {N}$ which is converging to $x_{0}$ , such that the sequence of function values $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ does not converge to $f(x_{0})$ . So there shall be $\lim _{n\to \infty }x_{n}=x_{0}$ but $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$ . In order for $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$ to hold, there are two cases to be distinguished:

• The sequence of function values $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ diverges.
• The sequence of function values $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ converges, but its limit is not $f(x_{0})$.

Therefore, a proof of discontinuity using the sequence criterion could take the following form: