Practical Electronics/Circuits Analysis/Kirchhoff laws
Kirchhoff laws were invented to describe the voltage and current relationship in an electric circuit. These laws are: Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL).
These are terms used specifically in Kirchhoff laws
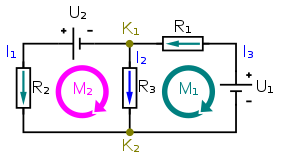
Node: Node or junction is a point in the circuit where two or more electrical elements are connected. This specifies a voltage level with a reference node in a circuit. (See K1, K2)
Branch: The continuous conducting path between two junctions which contains electrical element in a circuit is referred as branch. (k1 have branches R1-R3 / R1-U2)
Loop: In an electrical circuit a loop is an independent closed path in a circuit that follows the sequence of branches in such a way that it must start and ends with same node and it shouldn’t touch any other junction or node more than once. (See the path of M1 and M2)
Mesh: In an electrical circuit mesh is a loop that doesn’t contain any other loop in its interior. (See M1 , M2)
Kirchhoff’s Current Law (KCL)
[edit | edit source]
The algebraic sum of currents at any node is zero. Thus the current entering at a node must be equal to sum of current out of the node.
The "general" formulae is ,
(Note: The number of currents at note does not necessary amount to 5, maybe less or more)
where I1 and I2 refers to current entering at a node
and
I3 ,I 4 and I5 refers to current exiting at a node
Kirchhoff’s Voltage Law (KVL)
[edit | edit source]
Kirchhoff’s Voltage Law states that the algebraic sum of voltages in a closed path is equal to zero that is the sum of source voltages is equal to the sum of voltage drops in a circuit. If the current flows from higher potential to lower in an element, then we consider it as a voltage drop.
If the current flows from lower potential to higher potential, then we consider it as a voltage rise. Thus, the energy dissipated by the current must be equal to the energy given by the power supply in an electric circuit.
There are no general formula of Kirchoff's Voltage Law but based on examples shown, the formula can be described as :


