Puzzles/Segregation

Segregation type of puzzle is a type of puzzle that are different from the puzzle shown before whereas the main objective are not filling in the grid buat actually divide out the cells according to its category

Domino Set

• Draw lines to separate the grid to form a complete set of standard dominoes (28 pieces) , with exactly one of each domino
• A '0' represent blank on a traditional domino
• Use the checklist to help track which dominoes already being placed

• 
  Example of domino set puzzles
• 
  Domino set solutions
• 
  Checkoff list for the dominoes
• 
  Standard set of domino

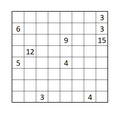
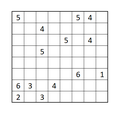
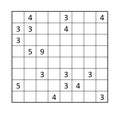
Rectangles

• Draw borders along some grid lines to divide the grid into a set of rectangles, such that each rectangles contain exactly one number
• All cells are within one rectangle
• The number inside each rectangle must be exactly equal to the number that grid cells contain.
• Example, no "4" would contain 1X4, 2X2 or 4X1 rectangle
• The name rectangle can be meant squares too

• 
  Example of rectangle puzzles
• 
  Example of rectangle solved puzzles

Spiral Galaxies

• Draw along some grid lines to form regions
• Each region must contain exactly one circles
• Each region must be symmetrical in such a way that if rotated 180 degrees around its circle then it would look exactly the same
• Each cells must be in exactly one region

Gallery

• Example of solved puzzles
  Example of solved puzzles

Rooms

• Each grid cells is considered to be a room
• Draw along some grid lines to build walls
• Build a wall that when standing in a room with a number in it, you can see that many rooms by looking along the row or column and DO NOT include the room itself
• All room are connected together so that walled off rooms or sections cannot be created

Gallery

• Example of solved puzzles
  Example of solved puzzles

Carpet set

• Draw borders along some grid lines to divide the grids into set of rectangles such that each number is inside exactly one rectangle
• The number inside each rectangle must be exactly equal to the number of grid cells that rectangle contains, for example "4" could be in 1X4, 2X2 and 4X1 rectangle
• Not all cells are necessarily contained within a rectangle
• Note that term rectangle includes 'square' too

• 
  Example of carpet set puzzles
• 
  Examples of solved carpet set puzzle

Sum Borders

• Draw borders along some grid lines to divide the grids into set of rectangles such that each number is inside exactly one rectangle
• All cells are within exactly one rectangle
• The number inside each rectangle must be exactly equal to the sum of the width and height of that rectangle, measured in cells. For example '5' could be within 1X4,2X3,3X2 or 4X1 rectangles.

• 
  Example of sum border puzzle
• 
  Example of solved puzzle