Social Statistics

An Introduction to Social Statistics

The children of rich parents usually grow up to be rich adults, and the children of poor parents usually grow up to be poor adults. This seems like a fundamental fact of social life, but is it true? And just how true is it? We've all heard stories of poor persons who make it rich (Oprah Winfrey, Jennifer Lopez, Steve Jobs) and rich persons who spend all their money and end up poor. The relationship between parents' income and children's income for a random sample of Americans is depicted in Figure 1-1. As you can see, parents' income and children's income are related, but with plenty of room for error. Rich parents tend to have rich children, but not all the time, and poor parents tend to have poor children, but not all the time. This kind of result is very common in the social sciences. Social science can explain a lot of things about our world, but it never explains them perfectly. There's always room for error.

The goal of social statistics is to explain the social world as simply as possible with as little error as possible. In Figure 1-1, it seems like parents' incomes explain their children's incomes pretty well, even if not perfectly. Some of the error in explaining children's incomes might come from errors in measurement. Persons don't always answer honestly when asked how much money they make. Persons might not even know for sure exactly how much money they made in any given year. It's impossible to predict the mistakes persons will make in answering social survey questions about their incomes, so no analysis of children's reported incomes will be perfectly accurate.

On the other hand, most of the error in Figure 1-1 probably has nothing to do with bad measurement. Most of the error is in explaining children's incomes probably comes from important determinants of income that have been left out of this analysis. There are many potential reasons why children's incomes may not correspond to their parents' incomes. For example, potential sources of error include things like:

Children may do better / worse in school than their parents did
Children may enter more / less well-paying professions than their parents did
Children may be more / less lucky in getting a job than their parents were
Children may be more / less ambitious than their parents were

A statistical analysis of income that included children's school performance, choice of profession, job luck, and ambition would have less error than the simple graph based just on parents' income, but it would also be much more complicated. Social statistics always involves trade-offs like this between complexity and error. Everything about the social world is determined by many different factors. A person's income level might result in part from job advice from a friend, getting a good recommendation letter, looking good on the day of an interview, being black, being female, speaking English with a strong accent, or a million other causes. Social statistics is all about coming up with ways to explain social reality reasonably well using just a few of these causes. No statistical model can explain everything, but if a model can explain most of the variability in persons' incomes based on just a few simple facts about them, that's pretty impressive.

This chapter lays out some of the basic building blocks of social statistics. First, social statistics is one of several approaches that social scientists use to link social theory to data about the world (Section 1.1). It is impossible to perform meaningful statistical analyses without first having some kind of theoretical viewpoint about how the world works. Second, social statistics is based on the analysis of cases and variables (Section 1.2). For any variable we want to study (like income), we have to have at least a few cases available for analysis—the more, the better. Third, social statistics almost always involves the use of models in which some variables are hypothesized to cause other variables (Section 1.3). We usually use statistics because we believe that one variable causes another, not just because we're curious. An optional section (Section 1.4) tackles the question of just how causality can be established in social statistics.

Finally, this chapter ends with an applied case study of the relationship between spending on education and student performance across the 50 states of the United States (Section 1.5). This case study illustrates how theory can be applied to data, how data are arranged into cases and variables, and how independent and dependent variables are causally related. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should have all the tools you need to start modeling the social world using social statistics.

1.1: Theory and Data

Theories determine how we think about the social world. All of us have theories about how the world works. Most of these theories are based on personal experience. That's alright: Isaac Newton is supposed to have developed the theory of gravity because he personally had an apple fall on his head. Personal experience can be a dangerous guide to social theory, since your experiences might be very difference from other persons' experiences. It's not a bad place to start, but social science requires that personal experiences be turned into more general theories that apply to other persons as well, not just to you. Generalization is the act of turning theories about specific situations into theories that apply to many situations. So, for example, you may think that you eat a lot of junk food because you can't afford to eat high-quality food. This theory about yourself could be generalized into a broader theory about persons in general:

Persons eat junk food because they can't afford to eat high-quality food.

Generalization from personal experience is one way to come up with theories about the social world, but it's not the only way. Sometimes theories come from observing others: you might see lots of fast food restaurants in poor neighborhoods and theorize that persons eat junk food because they can't afford to eat high-quality food. Sometimes theories are developed based on other theories: you might theorize that all persons want to live as long as possible, and thus conclude that persons eat junk food because they can't afford to eat high-quality food. Sometimes ideas just pop into your head: you're at a restaurant drinking a soda with unlimited free refills, and it just dawns on you that maybe persons eat junk food because they can't afford to eat high-quality food. However it happens, somehow you conceive of a theory. Conceptualization is the process of developing a theory about some aspect of the social world.

The main difference between the kinds of social commentary you might hear on radio or television and real social science is that in social science theories are scrutinized using formal statistical models. Statistical models are mathematical simplifications of the real world. The goal of statistical modeling is to explain complex social facts as simply as possible. A statistical model might be as simple as a graph showing that richer parents have richer children, as depicted in Figure 1-1. This graph is takes a very complex social fact (children's income) and explains it in very simple terms (it rises as parents' income rises) but with lots of room for error (many children are richer or poorer than their parents).

Social scientists use statistical models to evaluate different theories about how the world works. In our minds we all have our own theories about the social world, but in the real world we can't all be right. Before social scientists accept a theory, they carefully evaluate it using data about the real world. Before they can be evaluated, theories have to be turned into specific hypotheses about specific data. Operationalization is the process of turning a social theory into specific hypotheses about real data. The theory that persons eat junk food because they can't afford to eat high-quality food seems very reasonable, but it's too vague to examine using social statistics. First it has to be operationalized into something much more specific. Operationalization means answering questions like:

Which persons eat junk food? All persons in the world? All Americans? Poor Americans only?
What's junk food? Soda? Candy? Potato chips? Pizza? Sugar cereals? Fried chicken?
What's high-quality food? Only salads and home-made dinners? Or do steaks count too?
Is fresh-squeezed fruit juice a junk food (high in sugar) or a high-quality food (fresh and nutritious)?
What does "afford" mean? Literally not having enough money to buy something? What about other expenses besides food?
Whose behavior should we study? Individuals? Families? Households? Whole cities? Counties? States? Countries? The world?

For example, one way to study the relationship between junk food consumption and the affordability of high-quality food is to use state-level data. It can be very convenient to study US states because they are similar in many ways (they're all part of the same country) but they are also different enough to make interesting comparisons. There is also a large amount of data available for US states that is collected and published by US government agencies. For example, junk food consumption can be operationalized as the amount of soft drinks or sweetened snacks consumed in the states (both available from the US Department of Agriculture) and affordability can be operationalized using state median income. Most persons living in states with high incomes should be able to afford to eat better-quality food.

Data on state soft drink consumption per person and state median income are graphed in Figure 1-2. Each point in Figure 1-2 represents a state. A few sample states are labeled on the graph. This graph is called a scatter plot. Scatter plots are very simple statistical models that depict data on a graph. The scatter plot can be used to determine whether soft drink consumption rises, falls, or stays the same across the range of state income levels. In the scatter plot graphed in Figure 1-2, soft drink consumption tends to fall as income rises. This is consistent with the theory that persons buy healthy food when they can afford it, but eat unhealthy food when they are poorer. The theory may or may not be correct. The scatter plot provides evidence in support of the theory, but it does not conclusively prove the theory. After all, there may be many other reasons why soft drink consumption tends to be higher in the poorer states.

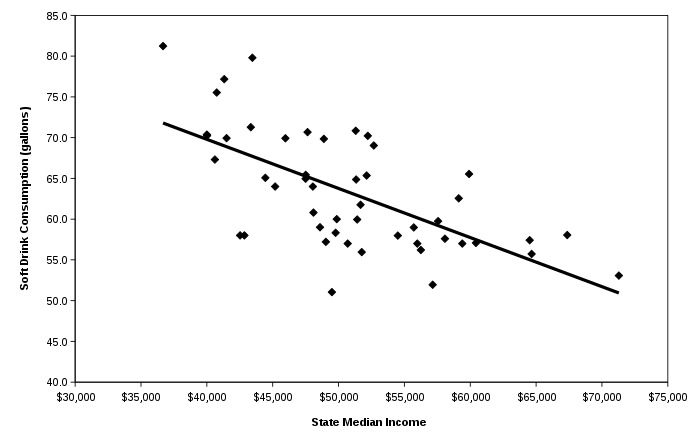
There is also a lot of error in the statistical model explaining soft drink consumption. There are many poor states that have very low levels of soft drink spending as well as many rich states that have very high levels of soft drink spending. So while the overall trend is that richer states have lower spending on soft drinks, there are many exceptions. This could be because the theory is wrong, but it also could be because there are many reasons why persons might consume soft drinks besides the fact that they are poor. For example, persons might consume soft drinks because:

They live in places with hot weather and consume a lot of all kinds of drinks
They eat out a lot, and tend to consume soft drinks at restaurants
They're trying to lose weight and are actually consuming zero-calorie soft drinks
They just happen to like the taste of soft drinks

All these reasons (and many others) may account for the large amount of error in the statistical model graphed in Figure 1-2.

Another way to operationalize the theory that theory that persons eat junk food because they can't afford to eat high-quality food is presented in Figure 1-3. In Figure 1-3, junk food consumption is operationalized as consumption of sweetened snack foods (cookies, snack cakes, candy bars, and the like). Again, the overall theory is that persons eat junk food because they can't afford to eat high-quality food, so state average income should be negatively related to the consumption of sweetened snack foods. In other words, as state average income goes up, sweetened snack food consumption should go down. But the data tell a different story: it turns out that there is essentially no relationship between state average income and sweetened snack consumption.

What went wrong here? Why is there no relationship between state average income and sweetened snack consumption? There are many possible reasons.

First, it may have been wrong to generalize from one person's experience (I eat junk food because I can't afford to eat high-quality food) to a general rule about society (persons eat junk food because persons can't afford to eat high-quality food). Second, it may have been wrong to conceptualize any relationship between affordability and junk food consumption at all (maybe junk food is actually more expensive than high-quality food). Third, it may have been wrong to operationalize junk food consumption at the state level (for example, it is possible that rich states actually contain lots of poor persons who eat lots of sweetened snacks). Fourth, it may have been wrong to use such a simple statistical model as a scatter plot (later chapters in this book will present much more sophisticated statistical models).

Because there are so many possible sources of error in social statistics, statistical analyses often lead to conflicting results like those reported in Figure 1-2 and Figure 1-3. Inconsistent, inconclusive, or downright meaningless results pop up all the time. The social world is incredibly complicated. Social theories are always far too simple to explain it all. Social statistics give us the opportunity to see just how well social theories perform out in the real world. In the case of our theory that persons eat junk food because they can't afford to eat high-quality food, social statistics tell us that there is some evidence to support the theory (soft drink consumption tends to be higher in poor states), but better theories are clearly needed to fully explain differences in persons' junk food consumption.

1.2: Cases and Variables

As the junk food example shows, when operationalizing theories into specific hypotheses in the social sciences the biggest obstacle is usually the difficulty of getting the right the data. Few quantitative social scientists are able to collect their own data, and even when they do they are often unable to collect the data they want. For example, social scientists who want to study whether or not persons can afford to buy high-quality food would ideally want to know all sorts of things to determine affordability. They would want to know persons' incomes, of course, but they would also want to know how much healthy foods cost in each person's neighborhood, how far persons would have to drive to get to a farm store or organic supermarket, whether or not they have a car, how many other expenses persons have besides food, etc. Such detailed information can be very difficult to collect, so researchers often make do with just income.

It is even more difficult to find appropriate data when researchers have to rely on data collected by others. The collection of social data is often done on a very large scale. For example, most countries conduct a population census at regular intervals. In the United States, this involves distributing short census questionnaires to over 100 million households every ten years. The longer, more detailed American Community Survey is sent to around 250,000 households every month. A further 60,000 households receive a detailed employment survey, the Current Population Survey. Other social data can also be very difficult and expensive to collect. The income data used in Figure 1-2 come from a national survey of 12,686 persons and their children who were surveyed almost every year for thirty years. The food consumption data used in Figures 1-2 and 1-3 come from barcode scans of products bought by 40,000 households across America. Obviously, no one person can collect these kinds of data on her own.

The good news is that enormous amounts of social survey and other social data can now be downloaded over the internet. All the data used in this textbook are freely available to the public from government or university websites. These public use datasets have been stripped of all personally identifying information like the names and addresses of individual respondents. Also very conveniently, the data in these datasets have usually been organized into properly formatted databases.

Databases are arrangements of data into variables and cases. When persons are interviewed in a survey, the raw data often have to be processed before they can be used. For example, surveys don't usually ask persons their ages, because (believe it or not) persons often get their ages wrong. Instead, survey takers ask persons their dates of birth. They also record the date of the survey. These two dates can then be combined to determine the respondent's age. The respondent's age is a sociologically meaningful fact about the respondent. Raw data like the respondent's birth date and interview date have been transformed into a variable that can be used in statistical models.

Variables are analytically meaningful attributes of cases. Cases are the individuals or entities about which data have been collected. Databases usually include one row of data for each case. Variables are arranged into columns. There may also be columns of metadata. Metadata are additional attributes of cases that are not meant to be included in analyses. A sample database including both metadata and variables is presented in Figure 1-4.

Figure 1-4: Data on income and nutrition for 48 US states plus the District of Columbia (Alaska and Hawaii excluded due to lack of data)
STATE_NAME	STATE_ABBR	MED_INCOME	LB_SNACKS	GAL_SODA	LB_FRUVEG
Alabama	AL	$40,751	111.6	75.5	168.3
Arizona	AZ	$49,863	109.0	60.0	157.0
Arkansas	AR	$40,001	104.3	70.4	147.3
California	CA	$58,078	105.7	57.6	201.8
Colorado	CO	$57,559	109.2	59.8	159.2
Connecticut	CT	$64,662	131.5	55.7	188.1
Delaware	DE	$56,252	134.6	56.2	218.2
District of Columbia	DC	$50,695	122.0	57.0	218.2
Florida	FL	$48,095	104.4	60.8	168.8
Georgia	GA	$51,673	107.1	61.8	198.4
Idaho	ID	$49,036	130.0	57.2	185.3
Illinois	IL	$52,677	127.8	69.0	198.0
Indiana	IN	$47,647	122.3	70.7	184.5
Iowa	IA	$51,339	121.1	64.9	171.2
Kansas	KS	$47,498	120.9	65.0	170.8
Kentucky	KY	$41,320	144.7	77.2	170.7
Louisiana	LA	$40,016	101.9	70.2	147.1
Maine	ME	$48,592	118.0	59.0	190.0
Maryland	MD	$67,364	125.1	58.0	218.5
Massachusetts	MA	$60,434	116.8	57.1	155.6
Michigan	MI	$51,305	122.5	70.8	181.2
Minnesota	MN	$59,910	120.5	65.5	172.8
Mississippi	MS	$36,674	112.5	81.2	160.2
Missouri	MO	$47,507	120.6	65.4	172.3
Montana	MN	$42,524	111.0	58.0	175.0
Nebraska	NE	$52,134	120.6	65.3	172.4
Nevada	NV	$54,500	111.5	58.0	175.3
New Hampshire	NH	$64,512	115.6	57.4	159.0
New Jersey	NJ	$71,284	135.8	53.1	201.1
New Mexico	NM	$42,850	111.0	58.0	175.0
New York	NY	$51,763	111.5	56.0	184.9
North Carolina	NC	$44,441	104.6	65.1	165.7
North Dakota	ND	$45,184	122.0	64.0	169.0
Ohio	OH	$48,884	122.6	69.8	185.0
Oklahoma	OK	$41,497	103.6	69.9	143.2
Oregon	OR	$49,495	111.0	51.0	173.8
Pennsylvania	PA	$51,416	130.0	60.0	203.7
Rhode Island	RI	$55,980	115.0	57.0	151.0
South Carolina	SC	$43,338	100.5	71.3	161.5
South Dakota	SD	$48,051	122.0	64.0	169.0
Tennessee	TN	$43,458	113.9	79.8	167.4
Texas	TX	$45,966	104.7	69.9	162.0
Utah	UT	$59,395	135.0	57.0	188.0
Vermont	VE	$55,716	117.8	59.0	187.1
Virginia	VA	$59,126	110.5	62.6	187.7
Washington	WA	$57,148	111.9	51.9	175.0
West Virginia	WV	$40,611	107.4	67.3	176.0
Wisconsin	WI	$52,223	121.3	70.2	183.9
Wyoming	WY	$49,777	114.0	58.3	172.7

The database depicted in Figure 1-4 was used to conduct the analyses reported in Figure 1-2 and Figure 1-3. The first two columns in the database are examples of metadata: the state name (STATE_NAME) and state abbreviation (STATE_ABBR). These are descriptive attributes of the cases, but they are not analytically meaningful. For example, we would not expect soda consumption to be determined by a state's abbreviation. The last four columns in the database are examples of variables. The first variable (MED_INCOME) is each state's median income. The other three variables represent annual state sweetened snack consumption in pounds per person (LB_SNACKS), soft drink consumption in gallons per person (GAL_SODA), and fruit and vegetable consumption in pounds per person (LB_FRUVEG). As in Figure 1-4, metadata are usually listed first in a database, followed by variables. The cases are usually sorted in order using the first metadata column as a case identifier. In this case, the data are sorted in alphabetical order by state name.

The cases in a database can be political units (like states or countries), organizations (like schools or companies), persons (like individuals or families), or any other kind of entity. The database that was used in Figure 1-1 is presented in Figure 1-5. In this database, the metadata appear in the first column (CHILD_ID) and the fifth column (MOTHER_ID). The gender of each child is reported in the third column (GENDER). Gender is recorded as "1" for men and "2" for women and mother's race is recorded as "1" for white and "2" for non-white. Income variables for the children's families (FAM_INC) and their mothers' families (PAR_INC) appear in the second and fifth columns. Notice that the incomes of the children's families are rounded off, while the incomes of the mothers' families are exact. Researchers using these data have to accept inconsistencies like this and work with them, since there's no way to go back and re-collect the data. We're stuck using the data as they exist in the database.

Figure 1-5: Data on income for a selection of 50 random children and their parents from the National Longitudinal Survey of Youth (NLSY)
CHILD_ID	FAM_INC	GENDER	M_RACE	MOTH_ID	PAR_INC
2001	$150,000	2	1	20	$113,750
4902	$90,000	1	1	49	$90,090
23102	$120,000	2	1	231	$85,811
25202	$68,000	1	1	252	$13,679
55001	$61,000	2	1	550	$71,344
76803	$100,000	2	1	768	$56,784
82802	$50,000	1	1	828	$64,246
97101	$59,000	2	1	971	$32,396
185301	$150,000	1	1	1853	$176,904
226801	$10,000	2	2	2268	$3,786
236901	$100,000	1	1	2369	$182,002
294903	$150,000	2	1	2949	$62,062
302301	$388,387	2	1	3023	$120,120
315101	$60,000	2	1	3151	$37,310
363502	$150,000	2	1	3635	$64,370
385101	$40,000	1	1	3851	$70,980
396204	$100,000	1	1	3962	$62,972
402803	$80,000	1	1	4028	$111,202
411001	$75,000	1	1	4110	$10,804
463102	$75,000	2	1	4631	$61,880
463801	$25,000	1	1	4638	$25,859
511403	$180,000	1	1	5114	$105,196
512302	$70,000	2	1	5123	$41,860
522402	$50,000	2	1	5224	$43,680
542402	$100,000	1	1	5424	$35,736
548301	$30,000	1	2	5483	$46,279
552601	$40,000	2	1	5526	$30,940
576601	$28,000	1	2	5766	$21,849
581101	$40,000	2	2	5811	$72,800
611601	$80,000	2	2	6116	$30,940
616802	$50,000	1	2	6168	$11,102
623801	$50,000	2	2	6238	$26,426
680702	$45,000	1	2	6807	$27,300
749801	$90,000	1	2	7498	$43,680
757802	$90,000	1	2	7578	$30,940
761702	$5,000	2	2	7617	$8,008
771002	$44,000	1	2	7710	$9,218
822603	$150,000	2	2	8226	$180,726
825902	$36,000	2	2	8259	$20,457
848803	$100,000	2	2	8488	$79,549
855802	$32,000	2	2	8558	$7,280
898201	$60,000	1	2	8982	$13,523
906302	$11,000	2	2	9063	$9,218
943401	$20,000	1	2	9434	$7,571
977802	$150,000	1	2	9778	$96,460
1002603	$32,000	2	2	10026	$30,476
1007202	$52,000	2	2	10072	$17,734
1045001	$60,000	2	2	10450	$78,315
1176901	$30,000	2	1	11769	$66,375
1200001	$80,000	1	1	12000	$70,525

Each case in this database is an extended family built around a mother–child pair. The children's family incomes include the incomes of their spouses, and the mothers' family incomes include the incomes of their spouses, but the mothers' spouses may or may not be the fathers of the children in the database. Since the data were collected on mother–child pairs, we have no way to know the incomes of the children's biological fathers unless they happen to have been married to the mothers in 1987 when the mothers' income data were collected. Obviously we'd like to know the children's fathers' incomes levels, but the data were never explicitly collected. If the parents were not married as of 1987, the biological fathers' data are gone forever. Data limitations like the rounding off of variables and the fact that variables may not include all the data we want are major sources of error in statistical models.

1.3: Dependent Variables and Independent Variables

In social statistics we're usually interested in using some variables to explain other variables. For example, in operationalizing the theory that persons eat junk food because they can't afford to eat high-quality food we used the variable "state median income" (MED_INCOME) in a statistical model (specifically, a scatter plot) to explain the variable "soft drink consumption" (GAL_SODA). In this simple model, we would say that soft drink consumption depends on state median income. Dependent variables are variables that are thought to depend on other variables in a model. They are outcomes of some kind of causal process. Independent variables are variables that are thought to cause the dependent variables in a model. It's easy to remember the difference. Dependent variables depend. Independent variables are independent; they don't depend on anything.

Whether a variable is independent or dependent is a matter of conceptualization. If a researcher thinks that one variable causes another, the cause is the independent variable and the effect is the dependent variable. The same variable can be an independent variable in one model but a dependent variable in another. Within any one particular model, however, it should be clear which variables are independent and which variables are dependent. The same variable can't be both: a variable can't cause itself.

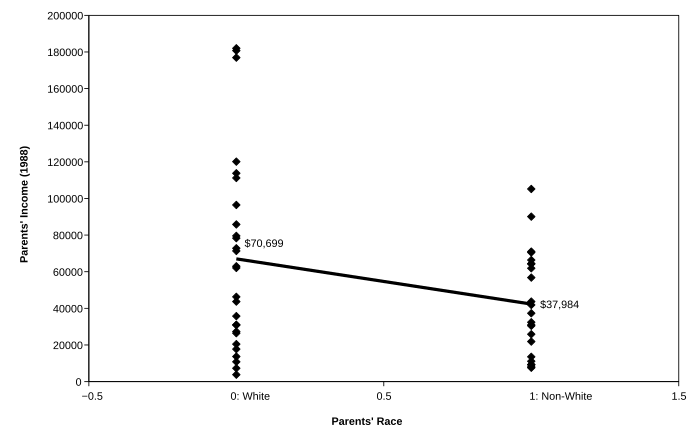
For an example of how a variable could change from independent to dependent, think back to Figure 1-1. In that figure, parents' income is the independent variable and children's income is the dependent variable (in the model, parents' income causes children's income). Parents' income, however, might itself be caused by other variables. We could operationalize a statistical model in which the parents' family income (the variable PAR_INC) depends on the parents' race (M_RACE). We use the mother's race to represent the race of both parents, since we don't have data for each mother's spouse (if any). A scatter plot of parents' family income by race is presented in Figure 1-6. Remember that the variable M_RACE is coded so that 0 = white and 1 = non-white. Clearly, the white parents had much higher family incomes (on average) than the non-white parents, almost twice as high. As with any statistical model, however, there is still a lot of error: race explains a lot in America, but it doesn't explain everything.

Just like parents' income, any variable can be either an independent variable or a dependent variable. It all depends on the context. All of the dependent variables and independent variables that have been used so far in this chapter are summarized in Figure 1-7. An arrow (→) has been used to indicate which variable is thought to cause which. Remember, in each model the independent variable causes the dependent variable. That's the same as saying that the dependent variables depend on the independent variables. Since parents' income has been used as both an independent variable (Figure 1-1) and as a dependent variable (Figure 1-6) it appears twice in the table. State median income has also been used twice, both times as an independent variable (Figure 1-2 and Figure 1-3).

Figure 1-7: Examples of dependent variables, independent variables, and models
Figure	Independent Variable	Dependent Variable	Model	Trend
Figure 1-1	Parents' income →	Children's income	Scatter plot	Up
Figure 1-2	State median income →	Soft drink consumption	Scatter plot	Down
Figure 1-3	State median income →	Sweetened snack consumption	Scatter plot	Up
Figure 1-6	Parents' race →	Parents' income	Scatter plot	Down

In each example reported in Table 1-1, the statistical model used to understand the relationship between the independent variable and the dependent variable has been a scatter plot. In a scatter plot, the independent variable is always depicted on the horizontal (X) axis. The dependent variable is always depicted on the vertical (Y) axis. A line has been drawn through the middle of the cloud of points on each scatter plot to help illustrate the general trend of the data. In Figure 1-1 the general trend is up: parents' income is positively related to children's income. In Figure 1-2 the general trend is down: state median income is negatively related to soft drink consumption. In Figure 1-3 and Figure 1-6 the trends are again up and down, respectively. Whether the trend is up or down, the existence of a trend indicates a relationship between the independent variable and the dependent variable.

A scatter plot is a very simple statistical model that helps show the overall relationship between one independent variable and one dependent variable. In future chapters, we will study more sophisticated statistical models. Many of them will allow for multiple independent variables of different kinds, but every model used in this book will have just one dependent variable. Models with multiple dependent variables exist, but they are much more complicated and won't be covered here.

1.4: Inferring Causality

Optional/advanced

Social scientists are almost always interested in making claims about causality, in claiming that one variable causes another. We suspect that sexism in the workplace leads to lower wages for women, that education leads to greater life fulfillment, that social inequality leads to higher levels of violence in society. The problem is that in the social sciences it is almost always impossible to prove that one variable causes another. Instead, social scientists must infer causality as best they can using the facts—and reasoning—at their disposal.

It is so difficult to establish causality in the social sciences because most social science questions cannot be studied using experiments. In an experiment, research subjects are randomly assigned to two groups, an experimental group and a control group. The subjects in the experimental group receive some treatment, while the subjects in the control group receive a different treatment. At the end of the experiment, any systematic difference between the subjects in the two groups must be due to differences in their treatments, since the two groups have otherwise identical backgrounds and experiences.

In the social sciences, experiments are usually impossible. For example, we strongly suspect that sexism in the workplace causes lower wages for women. The only way to know for sure whether or not this is true would be to recruit a group of women and randomly assign them to work in different workplaces, some of them sexist and some of them not. The workplaces would have to be identical, except for the sexism. Then, after a few years, we could call the women back to check up on their wages. Any systematic differences in women's wages between those who worked in sexist workplaces and those who worked in non-sexist workplaces could then be attributed to the sexism, since we would know for certain that there were no other systematic differences between the groups and their experiences.

Of course, experiments like this are impossible. As a substitute for experiments, social scientists conduct interviews and surveys. We ask women whether or not they have experienced sexism at work, and then ask them how much money they make. If the women who experience sexism make less money than the women who do not experience sexism, we infer that perhaps that difference may be due to actual sexism in the workplace.

Social scientists tend to be very cautious in making causal inferences, however, because many other factors may be at work. For example, it is possible that the women in the study who make less money tend incorrectly to perceive their workplaces as being sexist (reverse causality). It is even possible that high-stress working environments in which persons are being laid off result both in sexist attitudes among managers and in lower wages for everyone, including women (common causality). Many other alternatives are also possible. Causality is very difficult to establish outside the experimental framework.

Most social scientists accept three basic conditions that, taken together, establish that an independent variable actually causes a dependent variable. They are:

Correlation: when the independent variable changes, the dependent variable changes
Precedence: the independent variable logically comes before the dependent variable
Non-spuriousness: the independent variable and the dependent variable are not both caused by some other factor

Of the three conditions, correlation is by far the easiest to show. All of the scatter plots depicted in this chapter demonstrate correlation. In each case, the values of the dependent variable tends to move in one direction (either up or down) in correspondence with values of the independent variable.

Precedence can also be easy to demonstrate—sometimes. For example, in Figure 1-6 it is very clear that race logically comes before income. It wouldn't make any sense to argue the opposite, that persons' incomes cause their racial identities. At other times precedence can be much more open to debate. For example, many development sociologists argue that universal education leads to economic development: an educated workforce is necessary for development. It is possible, however, that the opposite is true, that economic development leads to universal education: when countries are rich enough to afford it, they pay for education for all their people. One of the major challenges of social policy formation is determining the direction of causality connecting variables.

Non-spuriousness, on the other hand, is almost always very difficult to establish. An observed relationship between two variables is called "spurious" when it doesn't reflect any real connection between the variables. For example, smoking tobacco can cause lung cancer and smoking tobacco can cause bad breath, but bad breath doesn't cause lung cancer. This general logic of spuriousness is depicted in Figure 1-8. In Figure 1-8, a spurious relationship exists between two variables in a statistical model. The real reason for the observed correlation between the independent variable and the dependent variable is that both are caused by a third, common-cause variable. Situations like this are very common in the social sciences. In order to be able to claim that one variable causes another, a social scientist must show that an observed relationship between the independent variable and the dependent variable is not spurious.

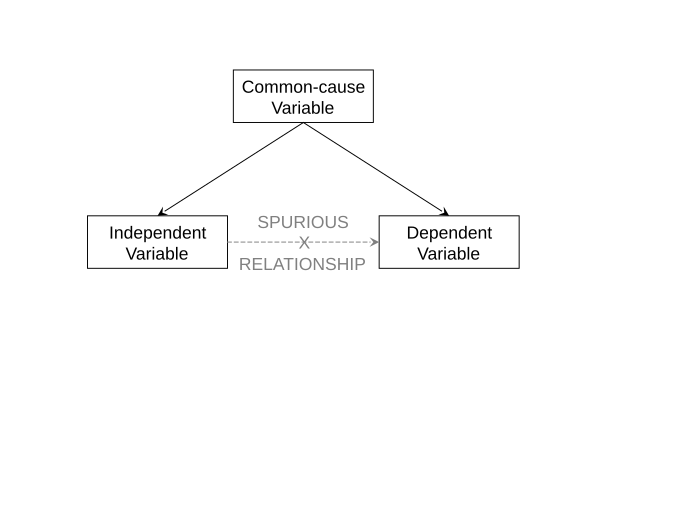
The problem with demonstrating non-spuriousness is that there can be many possible reasons why a relationship might be spurious. Returning to the relationship between parents' income and children's income, it is easy to see that there is a correlation between the two variables (Figure 1-1). It is also pretty obvious that parents' income precedes children's income. But what about non-spuriousness? There are many reasons why the relationship between parents' income and children's income might be spurious. One we've already seen: race. Non-white parents tend to have non-white children, so it's possible that instead of parent's income causing children's income, the truth is that the family's race determines both the parents' and the children's incomes (race is a common-cause variable). This could account for the observed correlation between parents' income and children's income. Other possible common-cause variables include:

The family's area of residence
The degree to which the family values money-making
Parents' educational levels (which can influence children's educational choices)
The parents' number of children

This last common-cause variable is an instructive example. In theory, having large numbers of children could force parents to stay home instead of working, lowering their incomes and making it difficult for them to afford college educations for their children, who could then have lower incomes as well. This might seem to most reasonable persons like a very unlikely scenario. The problem is that different persons have different ideas about what is reasonable. In order to establish the non-spuriousness of a relationship, researchers don't just have to convince themselves. They have to convince others, and everyone has a different idea of what might possibly create a spurious relationship between two variables. In the end, it is impossible to prove non-spuriousness. Instead, social scientists argue until they reach a consensus—or they just keep arguing. Causality is always subject to debate.

1.5: Case Study: Education Spending and Student Performance

Everyone knows that there are good schools and there are bad schools. The first question most parents ask when they're looking at a new home is "how are the schools?" Common sense suggests that the good schools are, on average, the rich schools. Everyone wants their children to go to schools that have brand-new computer labs, impressive sports facilities, freshly painted hallways, and nice green lawns. Parents also want their kids to receive individualized attention in small classes taught by talented, experienced teachers with master's degrees and doctorates. Active band, chorus, and art programs are also a plus. All this takes money.

A reasonable generalization from the observation that parents want to send their kids to schools that cost a lot of money to run is that states that spend more money on education will have better schools than states that spend less money on education. This generalization can be conceptualized into the theory that overall student performance depends (at least in part) on the amount of money a state spends on each student. This theory can be examined using data from the US National Center for Education Statistics (NCES). A database downloaded from the NCES website is reproduced in Figure 1-9. The cases are the 50 US states. There are two metadata columns (STATE and ABBR) and three variables (SPEND, READ_NAT, and MATH):

SPEND – Total state and local education spending per pupil
READ_NAT – State-average reading scores for native English-speaking 8th grade students
MATH – State-average math scores for all 8th grade students

Figure 1-9: Data on education spending and student performance for 50 U. S. states
STATE	ABBR	SPEND	READ_NAT	MATH
Alabama	AL	$10,356	255.5	268.5
Alaska	AK	$17,471	263.7	283.0
Arizona	AZ	$9,457	260.8	277.3
Arkansas	AR	$9,758	258.9	276.0
California	CA	$11,228	261.5	270.4
Colorado	CO	$10,118	268.5	287.4
Connecticut	CT	$16,577	272.8	288.6
Delaware	DE	$13,792	265.6	283.8
District of Columbia	DC	$17,394	243.2	253.6
Florida	FL	$10,995	265.3	279.3
Georgia	GA	$11,319	260.9	277.6
Hawaii	HI	$14,129	256.9	273.8
Idaho	ID	$7,965	266.4	287.3
Illinois	IL	$12,035	265.6	282.4
Indiana	IN	$11,747	266.1	286.8
Iowa	IA	$11,209	265.6	284.2
Kansas	KS	$11,805	268.4	288.6
Kentucky	KY	$9,848	267.0	279.3
Louisiana	LA	$11,543	253.4	272.4
Maine	ME	$13,257	267.9	286.4
Maryland	MD	$15,443	267.5	288.3
Massachusetts	MA	$15,196	274.5	298.9
Michigan	MI	$11,591	262.4	278.3
Minnesota	MN	$12,290	271.8	294.4
Mississippi	MS	$8,880	251.5	265.0
Missouri	MO	$11,042	267.0	285.8
Montana	MT	$10,958	271.4	291.5
Nebraska	NE	$11,691	267.8	284.3
Nevada	NV	$10,165	257.4	274.1
New Hampshire	NH	$13,019	271.0	292.3
New Jersey	NJ	$18,007	272.9	292.7
New Mexico	NM	$11,110	258.5	269.7
New York	NY	$19,081	266.0	282.6
North Carolina	NC	$8,439	261.1	284.3
North Dakota	ND	$11,117	269.5	292.8
Ohio	OH	$12,476	268.8	285.6
Oklahoma	OK	$8,539	260.4	275.7
Oregon	OR	$10,818	267.8	285.0
Pennsylvania	PA	$13,859	271.2	288.3
Rhode Island	RI	$15,062	261.3	277.9
South Carolina	SC	$10,913	257.5	280.4
South Dakota	SD	$9,925	270.4	290.6
Tennessee	TN	$8,535	261.3	274.8
Texas	TX	$9,749	263.2	286.7
Utah	UT	$7,629	267.2	284.1
Vermont	VT	$16,000	272.6	292.9
Virginia	VA	$11,803	266.6	286.1
Washington	WA	$10,781	268.7	288.7
West Virginia	WV	$11,207	254.9	270.4
Wisconsin	WI	$12,081	266.7	288.1
Wyoming	WY	$18,622	268.6	286.1

The theory that overall student performance depends on the amount of money a state spends on each student can be operationalized into two specific hypotheses:

State spending per pupil is positively related to state average reading scores
State spending per pupil is positively related to state average mathematics scores

In Figure 1-10 and Figure 1-11, scatter plots are used as statistical models for relating state spending to state reading and math scores. The dependent variable in Figure 1-10 is READ_NAT (reading performance for native English-speaking students) and the dependent variable in Figure 1-11 is MATH (mathematics performance). The independent variable in both figures is SPEND. In both figures state average scores do tend to be higher in states that spend more, but there is a large amount of error in explaining scores. There are probably many other determinants of student test scores besides state spending. Scores might be affected by things like parental education levels, family income levels, levels of student drug abuse, and whether or not states "teach to the test" in an effort to artificially boost results. Nonetheless, it is clear that (on average) the more states spend, the higher their scores.

The results of these data analyses tend to confirm the theory that overall student performance depends (at least in part) on the amount of money a state spends on each student. This theory may or may not really be true, but the evidence presented here is consistent with the theory. The results suggest that if states want to improve their student test scores, they should increase their school budgets. In education, as in most things, you get what you pay for.

Chapter 1 Key Terms

Conceptualization is the process of developing a theory about some aspect of the social world.
Cases are the individuals or entities about which data have been collected.
Databases are arrangements of data into variables and cases.
Dependent variables are variables that are thought to depend on other variables in a model.
Generalization is the act of turning theories about specific situations into theories that apply to many situations.
Independent variables are variables that are thought to cause the dependent variables in a model.
Metadata are additional attributes of cases that are not meant to be included in analyses.
Operationalization is the process of turning a social theory into specific hypotheses about real data.
Scatter plots are very simple statistical models that depict data on a graph.
Statistical models are mathematical simplifications of the real world.
Variables are analytically meaningful attributes of cases.

Linear Regression Models

Persons all over the world worry about crime, especially violent crime. Americans have more reason to worry than most. The United States is a particularly violent country. The homicide rate in the United States is roughly three times that in England, four times that in Australia, and five times that in Germany. Japan, a country of over 125 million persons, experiences fewer murders per year than Pennsylvania, with fewer than 12.5 million persons. Thankfully, American murder rates have fallen by almost 50% in the past 20 years, but they're still far too high.

Violent crime is, by definition, traumatic for victims and their families. A person who has been a victim of violent crime may never feel truly safe in public again. Violent crime may also be bad for society. Generalizing from the individual to the social level, if persons feel unsafe, they may stay home, avoid public places, and withdraw from society. This concern can be conceptualized into a formal theory: where crime rates are high, persons will feel less safe leaving their homes. A database that can be used to evaluate this theory has been assembled in Figure 2-1 using data available for download from the Australian Bureau of Statistics website. Australian data have been used here because Australia has just 8 states and territories (versus 50 for the United States), making it easier to label specific states on a scatter plot.

Figure 2-1: Data on crime and other social indicators for 8 Australian states and territories, 2008
STATE_TERR	CODE	VICTIM_PERS	UNSAFE_OUT	VICTIM_VIOL	STRESS	MOVED5YR	MED_INC
Australian Capital Territory	ACT	2.8	18.6	9.9	62.1	39.8	$712
New South Wales	NSW	2.8	17.4	9.3	57.0	39.4	$565
Northern Territory	NT	5.7	30.0	18.2	63.8	61.3	$670
Queensland	QLD	3.0	17.3	13.5	64.4	53.9	$556
South Australia	SA	2.8	21.8	11.4	58.2	38.9	$529
Tasmania	TAS	4.1	14.3	9.8	59.1	39.6	$486
Victoria	VIC	3.3	16.8	9.7	57.5	38.8	$564
Western Australia	WA	3.8	20.9	12.8	62.8	47.3	$581

The cases in the Australian crime database are the eight states and territories of Australia. The columns include two metadata items (the state or territory name and postal code). Six variables are also included:

VICTIM_PERS – The percent of persons who were the victims of personal crimes (murder, attempted murder, assault, robbery, and rape) in 2008
UNSAFE_OUT – The percent of persons who report feeling unsafe walking alone at night after dark
VICTIM_VIOL – The percent of persons who report having been the victim of physical or threatened violence in the past 12 months
STRESS – The percent of persons who report having experienced at least one major life stressor in the past 12 months
MOVED5YR – The percent of persons who have moved in the previous 5 years
MED_INC – State median income

The theory that where crime rates are high, persons will feel less safe leaving their homes can be operationalized using these data into the specific hypothesis that the relationship between the variables VICTIM_PERS and UNSAFE_OUT will be positively related across the 8 Australian states and territories. In this statistical model, VICTIM_PERS (the crime rate) is the independent variable and UNSAFE_OUT (persons' feelings of safety) is the dependent variable. The actual relationship between the two variables is plotted in Figure 2-2. Each point in the scatter plot has been labeled using its state postal code. This scatter plot does, in fact, show that the relationship is positive. This is consistent with the theory that where crime rates are high, persons will feel less safe leaving their homes.

As usual, Figure 2-2 includes a reference line the runs through the middle of all of the data points. Also as usual, there is a lot of error in the scatter plot. Fear of going out alone at night does rise with the crime rate, but not in every case. To help clarify the overall trend in fear of going out, Figure 2-2 also includes a new, additional piece of information: the amount of error that is associated with each observation (each state). Instead of thinking of a scatter plot as just a collection of points that trends up or down, it is possible to think of a scatter plot as a combination of trend (the line) and error (deviation from the line). This basic statistical model—a trend plus error—is the most widely used statistical model in the social sciences.

In Figure 2-2, three states fall almost exactly on the trend line: New South Wales, Queensland, and Western Australia. The persons in these three states have levels of fear about going out alone at night that are just what might be expected for states with their levels of crime. In other words, there is almost no error in the statistical model for fear in these states. Persons living in other states and territories have more fear (South Australia, Australian Capital Territory, Northern Territory) or less fear (Victoria, Tasmania) than might be expected based on their crime rates. Tasmania in particular has relatively high crime rates (the second highest in Australia) but very low levels of fear (the lowest in Australia). This means that there is a lot of error in the statistical model for Tasmania. While there is definitely an upward trend in the line shown in Figure 2-2, there is so much error in individual cases that we might question just how useful actual crime rates are for understanding persons' feelings of fear about going out at night.

This chapter introduces the linear regression model, which divides the relationship between a dependent variable and an independent variable into a trend plus error. First and foremost, the linear regression model is just a way of putting a line on a scatter plot (Section 2.1). There are many possible ways to draw a line through data, but in practice the linear regression model is the one way that is used in all of social statistics. Second, line on a scatter plot actually represents a hypothesis about how the dependent variable is related to an independent variable (Section 2.2). Like any line, it has a slope and an intercept, but social scientists are mainly interested in evaluating hypotheses about the slope. Third, it's pretty obvious that a positive slope means a positive relationship between the two variables, while a negative slope means a negative relationship (Section 2.3). The steeper the slope, the more important the relationship between the two variables is likely to be. An optional section (Section 2.4) explains some of the mathematics behind how regression lines are actually drawn.

Finally, this chapter ends with an applied case study of the relationship between property crime and murder rates in the United States (Section 2.5). This case study illustrates how linear regression models are used to put lines on scatter plots, how hypotheses about variables are turned into hypotheses about the slopes of these lines, and the difference between positive and negative relationships. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should have a basic understanding of how regression models can shed light on the relationships connecting independent and dependent variables in the social sciences.

2.1. Introducing the Linear Regression Model

When social scientists theorize about the social world, they don't usually theorize in straight-line terms. Most social theorists would never come up with a theory that said "persons' fear of walking along at night will rise in exactly a straight line as the crime rate in their neighborhoods rise." Instead, theories about the social world are much more vague: "persons will feel less safe leaving their homes where crime rates are high." All the theories that were examined in Chapter 1 were also stated in vague language that said nothing about straight lines:

Rich parents tend to have rich children
Persons eat junk food because they can't afford to eat high-quality food
Racial discrimination in America leads to lower incomes for non-whites
Higher spending on education leads to better student performance on tests

When theories say nothing about the specific shape of the relationship between two variables, a simple scatter plot is—technically—the appropriate way to evaluate them. With one look at the scatter plot anyone can see whether the dependent variable tends to rise, fall, or stay the same across values of the independent variable. The real relationship between the two variables might be a line, a curve, or an even more complicated pattern, but that is unimportant. The theories say nothing about lines or curves. The theories just say that when the independent variable goes up, the dependent variable goes up as well.

However, there are problems with scatter plots. Sometimes it can be hard to tell whether they trend upwards or not. For example, many Americans believe that new immigrants to America have large numbers of children, overwhelming schools and costing the taxpayers a lot of money. Figure 2-3 plots the relationship between birth rates (independent variable) and levels of international immigration (dependent variable) for 3193 US counties. Does the birth rate rise with greater immigration? It's hard to say from just the scatter plot, without a line. It turns out that birth rates do rise with immigration rates, but only very slightly.

As Figure 2-3 illustrates, another problem with scatter plots is that they become difficult to read when there are a large number of cases in the database being analyzed. Scatter plots also become difficult to read when there is more than one independent variable, as there will be later in this book. The biggest problem with using scatter plots to evaluate theories, though, is that different persons might have different opinions about then. One person might see a rising trend while someone else thinks the trend is generally flat or declining. Without a reference line to give a firm answer, it may be impossible to reach agreement on whether the theory being evaluated is or is not correct. For these (and other) reasons, social scientists don't usually rely on scatter plots. Scatter plots are widely used in the social sciences, but they are used to get an overall impression of the data, not to evaluate theories.

Instead, social scientists evaluate theories using straight lines like the reference lines that were drawn on the scatter plots above and in Chapter 1. These lines are called regression lines, and are based on statistical models called linear regression models. Linear regression models are statistical models in which expected values of the dependent variable are thought to rise or fall in a straight line according to values of the independent variable. Linear regression models (or just "regression models") are statistical models, meaning that they mathematical simplifications of the real world. Real variables may not rise or fall in a straight line, but in the linear regression model we simplify things to focus only on this one aspect of variables.

Of course, dependent variables don't really rise or fall in straight lines as regression models would suggest. Social scientists use straight lines because they are convenient, even though they may not always be theoretically appropriate. Other kinds of relationships between variables are possible, but there are many good reasons for using straight lines instead. Some of them are:

A straight line is the simplest way two variables could be related, so it should be used unless there's a good reason to suspect a more complicated relationship
Straight lines can be compared using just their slopes and intercepts (you don't need every piece of data, as with comparing scatter plots)
Usually there's so much error in social science models that we can't tell the difference between a straight line relationship and other relationships anyway

The straight line a linear regression model is drawn through the middle of the cloud of points in a scatter plot. It is drawn in such a way that each point along the line represents the most likely value of the dependent variable for any given value of the independent variable. This is the value that the dependent variable would be expected to have if there were no error in the model. Expected values are the values that a dependent variable would be expected to have based solely on values of the independent variable. Figure 2-4 depicts a linear regression model of persons' fear of walking along at night. The dependent variable from Figure 2-2, the percent of persons who feel unsafe, is regressed on a new independent variable, the percent of persons who reported experiencing violence personally. There is less error in Figure 2-4 than we saw in Figure 2-2. Tasmania in particular now falls very close to the reference line of expected values.

The expected values for the percent of persons who feel unsafe walking at night have been noted right on the scatter plot. They are the values of the dependent variable that would have been expected based on the regression model. For example, in this model the expected percentage of persons who feel unsafe walking at night in Tasmania would be 16.9%. In other words, based on reported levels of violence experienced by persons in Tasmania, we would expect about 16.9% of Tasmanians to feel unsafe walking alone at night. According to our data, 14.3% of persons in Tasmania report feeling unsafe walking at night (see the variable UNSAFE_OUT in Figure 2-1 and read across the row for Tasmania). Since the regression model predicted 16.9% and the actual value was 14.3%, the error for Tasmania in Figure 2-4 was 2.6% ( $16.9\%-14.3\%=2.6\%$ ).

Regression error is the degree to which an expected value of a dependent variable in a linear regression model differs from its actual value. Regression error is expressed as deviation from the trend of the straight line relationship connecting the independent variable and the dependent variable. In general, regression models that have very little regression error are preferred over regression models that have a lot of regression error. When there is very little regression error, the trend of the regression line will tend to be steeper and the relationship between the independent variable and the dependent variable will tend to be stronger.

There is a lot of regression error in the regression model depicted in Figure 2-4, but less regression error than was observed in Figure 2-2. In particular, the regression error for Tasmania in Figure 2-2 was 7.1%—much higher than in Figure 2-4. This suggests that persons' reports of experiencing violence personally are better predictors of persons' feelings of safety at night than are the actual crime rates in a state. Persons' experiences of safety and fear are very personal, not necessarily based on crime statistics for society as a whole. If policymakers want to make sure that persons feel safe enough to go out in public, they have to do more than just keep the crime rate down. They also have to reduce persons' personal experiences—and persons' perceptions of their personal experiences—of violence and crime. This may be much more difficult to do, but also much more rewarding for society. Policymakers should take a broad approach to making society less violent in general instead of just putting potential criminals in jail.

2.2: The Slope of a Regression Line

In the social sciences, even good linear regression models like that depicted in Figure 2-4 tend to have a lot of error. A major goal of regression modeling is to find an independent variable that fits the dependent variable with more trend and less error. An example of a relationship that is almost all trend (with very little error) is depicted in Figure 2-5. The scatter plot in Figure 2-5 uses state birth rates as the independent variable and state death rates as the dependent variable. States with high birth rates tend to have young populations, and thus low death rates. Utah has been excluded because its very high birth rate (over 20 children for every 1000 persons every year) doesn't fit on the chart, but were Utah included its death rate would fall very close to the regression line. One state has an exceptionally high death rate (West Virginia) and one state has an exceptionally low death rate (Alaska).

Thinking about scatter plots in terms of trends and error, the trend in Figure 2-5 is clearly down. Death rates fall as birth rates rise, but by how much? The slope of the regression line gives the answer. Remember that the regression line runs through the expected values of the dependent variable. Slope is the change in the expected value of the dependent variable divided by the change in the value of the independent variable. In other words, it is the change in the regression line for every one point increase in the independent variable. In Figure 2-5, when the independent variable (birth rate) goes up by 1 point, the expected value of the dependent variable (death rate) down by 0.4 points. The slope of the regression line is thus −0.4 / 1, or −0.4. The slope is negative because the line trends down. If the line trended up, the slope would be positive.

An example of a regression line with a positive slope is depicted in Figure 2-6. This line reflects a simple theory of why persons relocate to new communities. Americans are very mobile—much more mobile than persons in most other countries—and frequently move from place to place within America. One theory is that persons go where the jobs are: persons move from places that have depressed economies to places that have vibrant economies. In Figure 2-6, this theory has be operationalized into the hypothesis that counties with higher incomes (independent variable) tend to attract the most migration (dependent variable). In other words, county income is positively related to migration. Figure 2-6 shows that this hypothesis is correct—at least for one state (South Dakota). The slope of the regression line in Figure 2-6 indicates that when county income goes up by $10,000, migration tends to go up by around 8%. The slope is actually $8/10000=.0008$ .

The positive slope of the regression line in Figure 2-6 doesn't mean that persons always move to counties that have the highest income levels. There is quite a lot of error around the regression line. Lincoln County especially seems to far outside the range of the data from the other counties. Lincoln County is South Dakota's richest and its third most populous. It has grown rapidly over the past ten years as formerly rural areas have been developed into suburbs of nearby Sioux Falls in Minnehaha County. Many other South Dakota counties have highly variable migration figures because they are so small that the opening or closing of one employer can have a big effect on migration. Of the 66 counties in South Dakota, 49 are home to fewer than 10,000 persons. So it's not surprising that the data for South Dakota show a high level of regression error.

If it's true that persons move from places that have depressed economies to places that have expanding economies, the relationship between median income and net migration should be positive in every state, not just South Dakota. One state that is very different from South Dakota in almost every way is Florida. Florida has only two counties with populations under 10,000 persons, and the state is on average much richer than South Dakota. More importantly, lots of persons move to Florida for reasons that have nothing to do with jobs, like climate and lifestyle. Since many persons move to Florida when they retire, the whole theory about jobs and migration may be irrelevant there. To find out, Figure 2-7 depicts a regression of net migration rates on median county income for 67 Florida counties.

As expected, the Florida counties have much more regression error than the South Dakota counties. They also have a smaller slope. In Florida, every $10,000 increase in median income is associated with a 5% increase in the net migration rate, for a slope of $5/10000=.0005$ . This is just over half the slope for South Dakota. As in South Dakota, one county is growing much more rapidly than the rest of the state. Flagler County in Florida is growing for much the same reason as Lincoln County in Nebraska: it is a formerly rural county that is rapidly developing. Nonetheless, despite the fact that the relationship between income and migration is weaker in Florida than in South Dakota, the slope of the regression line is still positive. This adds more evidence in favor of the theory that persons move from places that have depressed economies to places that have vibrant economies.

2.3: Outliers and Robustness

Because there is so much error in the statistical models used by social scientists, it is not uncommon for different operationalizations of the same theory to give different results. We saw this in Chapter 1 when different operationalizations of junk food consumption gave different results for the relationship between state income and junk food consumption (Figure 1-2 versus Figure 1-3). Social scientists are much more impressed by a theory when the theory holds up under different operationalization choices, as in Figure 2.6 and Figure 2.7. Ideally, all statistical models that are designed to evaluate a theory would yield the same results, but in reality they do not. Statistical models can be particularly unstable when they have high levels of error. When there is a lot of error in the model, small changes in the data can lead to big changes in model results.

Robustness is the extent to which statistical models give similar results despite changes in operationalization. With regard to linear regression models, robustness means that the slope of the regression line doesn't change much when different data are used. In a robust regression model, the slope of the regression line shouldn't depend too much on what particular data are used or the inclusion or exclusion of any one case. Linear regression models tend to be most robust when:

They are based on large numbers of cases
There is relatively little regression error
All the cases fall neatly in a symmetrical band around the regression line

Regression models based on small numbers of cases with lots of error and irregular distributions of cases can be very unstable (not robust at all). Such a model is depicted in Figure 2-8. Many persons feel unsafe in large cities because they believe that crime, and particular murder, is very common in large cities. After all, in big cities like New York there are murders reported on the news almost every day. On the other hand, big cities by definition have lots of persons, so their actual murder rates (murders per 100,000 persons) might be relatively low. Using data on the 10 largest American cities, Figure 2-8 plots the relationship between city size and murder rates. The regression line trends downward with a slope of −0.7: as the population of a city goes up by 1 million persons, the murder rate goes down by 0.7 per 100,000. The model suggests that bigger cities are safer than smaller ones.

However, there are several reasons to question the robustness of the model depicted in Figure 2-8. Evaluating this model against the three conditions that are associated with robust models, it fails on every count. First, the model is based on a small number of cases. Second, there is an enormous amount of regression error. Third and perhaps most important, the cases do not fall neatly in a symmetrical band around the regression line. Of the ten cities depicted in Figure 2-8, eight are clustered on the far left side of the scatter plot, one (Los Angeles) is closer to the middle but still in the left half, and one (New York) is far on the extreme right side. New York is much larger than any other American city and falls well outside the cloud of points formed by the rest of the data. It stands alone, far away from all the other data points.

Outliers are data points in a statistical model that fall far away from most of the other data points. In Figure 2-8, New York is a clear outlier. Statistical results based on data that include outliers often are not robust. One outlier out of a hundred or a thousand points usually doesn't matter too much for a statistical model, but one outlier out of just ten points can have a big effect. Figure 2-9 plots exactly the same data as Figure 2-8, but without New York. The new regression line based on the data for the 9 remaining cities has a completely different slope from the original regression line. When New York was included, the slope was negative (−0.7), which indicated that larger cities were safer. With New York excluded, the slope is positive (0.8), indicating that larger cities are more dangerous. The relationship between city size and murder rates clearly is not robust.

It is tempting to argue that outliers are "bad" data points that should always be excluded, but once researchers start excluding points they don't like it can be hard to stop. For example, in Figure 2-9 after New York has been excluded there seems to be a new outlier, Philadelphia. All the other cities line up nicely along the trend line, with Philadelphia sitting all on its own in the upper left corner of the scatter plot. Excluding Philadelphia makes the slope of the regression line even stronger: it increases from 0.8 to 2.0. Then, with Philadelphia gone, Los Angeles appears to be an outlier. Excluding Los Angeles raises the slope even further, to 6.0. The danger here is obvious. If we conduct analyses only on the data points we like, we end up with a very skewed picture of the real relationships connecting variables out in the real world. Outliers should be investigated, but robustness is always an issue for interpretation, not something that can be proved by including or excluding specific cases.

2.4. Least Squared Error

Optional/advanced

In linear regression models, the regression line represents the expected value of the dependent variable for any given value of the independent variable. It makes sense that the most likely place to find the expected value of the dependent variable would be right in the middle of the scatter plot connecting it to the independent variable. For example, in Figure 2-5 the most likely death rate for a state with a birth rate of 15 wouldn't be 16 or 0, but somewhere in the middle, like 8. The death rate indicated by the regression line seems like a pretty average death rate for a state falling in the middle of the range in its birth rate. This seems reasonable so far as it goes. Obviously the regression line has to go somewhere in the middle, but how do we decide exactly where to draw it? One idea might be to draw the regression line so as to minimize the amount of error in the scatter plot. If a scatter plot is a combination of trend and error, it makes sense to want as much trend and as little error as possible. A line through the very middle of a scatter plot must have less error than other lines, right? Bizarrely, the answer is no. This strange fact is illustrated in Figure 2-10, Figure 2-11, and Figure 2-12. These three figures show different lines on a very simple scatter plot. In this scatter plot, there are just four data points:

X = 1, Y = 2
X = 1, Y = 8
X = 5, Y = 5
X = 5, Y = 8

The actual regression line connecting the independent variable (X) to the dependent variable (Y) is graphed in Figure 2-10. This line passes right through the middle of all four points. Each point is 4 units away from the regression line, so the regression error for each point is 4. The total amount of error for the whole scatter plot is $4+4+4+4=16$ . No other line could be drawn on the scatter plot that would result in less error. So far so good.

The problem is that the regression line (A) isn't the only line that minimizes the amount of error in the scatter plot. Figure 2-11 depicts another line (B). This line doesn't quite run through the middle of the scatter plot. Instead, it's drawn closer to the two low points and farther away from the two high points. It's clearly not as good a line as the regression line, but it turns out to have the same amount of error. The error associated with line B is $2+6+2+6=16$ . It seems that both line A and line B minimize the amount of error in the scatter plot.

That's not all. Figure 2-12 depicts yet another line (C). Line C is an even worse line than line B. It's all the way at the top of the scatter plot, very close to the two high points and very far away from the two low points. It's not at all in the middle of the cloud of points. But the total error is the same: $1+7+1+7=16$ . In fact, any line that runs between the points—any line at all—will give the same error. Many different trends give the same error. This makes it impossible to choose any one line based just on its total error. Another method is necessary.

That method that is actually used to draw regression lines is to draw the line that has the least amount of squared error. Squared error is just that: the error squared, or multiplied by itself. So for example if the error is 4, the squared error is 16 ( $4^{2}=4x4=16$ ). For line A in Figure 2-10, the total squared error is $4^{2}+4^{2}+4^{2}+4^{2}$ or $16+16+16+16=64$ . For line B in Figure 2-11, the total squared error is $2^{2}+6^{2}+2^{2}+6^{2}$ or $4+36+4+36=80$ . For line C in Figure 2-12, the total squared error is $1^{2}+7^{2}+1^{2}+7^{2}$ or $1+49+1+49=100$ . The line with the least squared error is line A, the regression line that runs through the very middle of the scatter plot. All other lines have more error.

It turns out that the line with the least squared error is always unique—there's only one line that minimizes the total amount of squared error—and always runs right through the center of the scatter plot. As an added bonus, computers can calculate regression lines using least squared error quickly and efficiently. The use of least squared error is so closely associated with linear regression models that they are often called "least squares regression models." All of the statistical models used in the rest of this book are based on the minimization of squared error. Least squared error is the mathematical principle that underlies almost all of social statistics.

2.5: Case Study: Property Crime and Murder Rates

Murder is a rare and horrific crime. It is a tragedy any time a human life is ended prematurely, but that tragedy is even worse when a person's death is intentional, not accidental. Sadly, some of the students using this textbook will know someone who was murdered. Luckily, most of us do not. But almost all of us know someone who has been the victim of a property crime like burglary or theft. Many of us have even been property crime victims ourselves. Property crimes are very common not just in the United States but around the world. In fact, levels of property crime in the US are not particularly high compared to other rich countries. This is odd, because the murder rate in the US are very high. It seems like all kinds of crime should rise and fall together. Do they?

One theory of crime might be that high rates of property crime lead to high rates of murder, as persons move from petty crime to serious crime throughout their criminal careers. Since international data on property crimes might not be equivalent from country to country, it makes sense to operationalize this theory using a hypothesis and data about US crime rates. A specific hypothesis linking property crime to murder would be the hypothesis that property crime rates are positively associated with murder rates for US cities with populations over 100,000 persons. This operationalization excludes small cities because it is possible that smaller cities might have no recorded crimes in any given year.

Data on crime rates of all kinds are available from the US Federal Bureau of Investigation (FBI). In Figure 2-13 these data are used to plot the relationship between property crime rates and murder rates for the 268 American cities with populations of over 100,000 persons. A linear regression model has been used to place a trend line on the scatter plot. The trend line represents the expected value of the murder rate for any given level of property crime. So for example in a city that has a property crime rate of 5,000 per 100,000 persons, the expected murder rate would be 10.2 murders per 100,000 persons. A few cities have murder rates that would be expected given their property crime rates, but there is an enormous amount of regression error. Murder rates are scattered widely and do not cluster closely around the regression line.

The slope of the regression line is positive, as expected. This tends to confirm the theory that high rates of property crime are associated with high rates of murder. Every increase of 1,000 in the property crime rate is associated, on average, with an increase of 2.7 in the murder rate. This is likely to be a robust result, since it is based on a large number of cases. On the other hand, there is a high level of error and the cases do not fall neatly in a symmetrical band around the regression line, so we might show some caution in interpreting our results. There is also one major outlier: New Orleans. The murder rate for New Orleans is far higher than that of any other US city, and New Orleans falls well outside the boundaries of the rest of the data. Excluding New Orleans, however, results in no change in the slope of the regression line, which remains 2.7 whether New Orleans is included or not.

Overall, the theory that high rates of property crime are associated with high rates of murder seems to be broadly valid for US cities as a whole, but the murder rate in any particular US city doesn't seem to correspond closely to the property crime rate. If they want to bring down their murder rates, it wouldn't hurt for US cities to try bringing down their property crime rates, but it likely wouldn't solve the problem. Cities with property crime rates in the range of 5,000–6,000 can have murder rates ranging anywhere from near zero to 30 or more. Policies to reduce murder rates should probably be targeted specifically at reducing violence in society, not broadly at reducing crime in general.

Chapter 2 Key Terms

Expected values are the values that a dependent variable would be expected to have based solely on values of the independent variable.
Linear regression models are statistical models in which expected values of the dependent variable are thought to rise or fall in a straight line according to values of the independent variable.
Outliers are data points in a statistical model that are far away from most of the other data points.
Regression error is the degree to which an expected value of a dependent variable in a linear regression model differs from its actual value.
Robustness is the extent to which statistical models give similar results despite changes in operationalization.
Slope is the change in the expected value of the dependent variable divided by the change in the value of the independent variable.

Using Regression to Make Predictions

Global warming is one of the greatest threats facing the world in the 21st century. Climate scientists are now absolutely certain that global warming is occurring and that it is related to human activity. The most obvious cause of global warming is fossil fuel consumption (though there are many other causes). Fossil fuels are minerals like coal, oil, and natural gas that were buried under the Earth's surface millions of years ago. Over the long history of the Earth, enormous amounts of carbon have been removed from the atmosphere by natural processes and deposited in the ground as minerals. Then, starting for real in the 1800s but gaining momentum in the 1900s through to today, we began digging and pumping these minerals out of the Earth to burn in our homes, power plants, and automobiles. Whenever we burn these carbon minerals, we release carbon dioxide (CO2) into the atmosphere, which leads to global warming. Global warming may seem like a topic for physical scientists to study, but really it is a social science topic. Physical scientists have told us how to stop global warming: if we just stop burning fossil fuels, the Earth will stop warming and eventually return to normal. The problem is that people don't want to stop burning fossil fuels. Changing people's attitudes and behavior is a social science problem. Figure 3-1 is an extract of data from a World Bank database called the World Development Indicators (WDI). The cases in the WDI database are countries. The columns of the database include two metadata items (the World Bank country code and the country name). Three variables are also included: CO2 -- Metric tons of carbon dioxide per person emitted by the country GNP -- The country's gross domestic product per capita, a measure of average national income CARS -- The number of passenger cars per 1000 residents of the country Countries were excluded where data were unavailable. For example, the WDI database included no passenger car data for Canada, so Canada is not included in Figure 3-1 or in the analyses to follow. Lack of data is the reason that the database includes data for only 51 out of the 200 or so countries of the world.

Presumably, countries that have more cars burn more gasoline. If so, we might hypothesize that the number of cars in a country should be positively related to its carbon dioxide emissions. Figure 3-2 shows a scatter plot of carbon dioxide emissions (dependent variable) versus passenger cars (independent variable) for the 51 countries represented in Figure 3-1. A linear regression model has been used to place a trend line through the data. While there is a lot of regression error around the trend line, the slope of the line is definitely positive. For every additional 100 cars in a country, the expected value of carbon dioxide emissions goes up by 1.25 tons per person. In other words, the slope of the regression line is 1.25 / 100 = .0125. This tends to support the hypothesis that numbers of cars are positively related to carbon dioxide emissions.

Two outliers in Figure 3-2 are the United States and Australia. Both have much higher carbon emissions than would be expected based on their numbers of cars. For the United States, this disconnect has a simple explanation: many Americans don't drive cars. They drive trucks and SUVs. These vehicles aren't included in the World Bank's "passenger cars" figures, but they certainly burn gasoline and produce carbon dioxide -- lots of it. For Australia, the explanation is more complicated, but Australia's high levels of carbon dioxide emissions are partly due to a heavy reliance on coal for electricity generation. Other countries that deviate from their expected levels of carbon emissions (Singapore, Kazakhstan) have their own stories. Overall, though, when countries have more cars they're likely to emit more carbon dioxide. This result is robust: removing Australia, the United States, Singapore, or Kazakhstan has little effect on the slope of the regression line. One interesting feature of Figure 3-2 is the expected value of carbon dioxide emissions when there are no cars in a country. This can be determined by finding zero on the passenger cars axis and reading up the graph until you hit the regression line. According to the regression line, when the number of cars is zero the expected level of carbon emissions is around 3 tons per capita. This implies that even if we gave up driving entirely, we would still have a problem with global warming. The reason is that there are many other sources of carbon emissions besides cars. We burn coal in power plants to generate electricity. We burn natural gas to heat our homes. Even without cars we would still have ships, trains, and airplanes burning oil. Solving global warming is going to be very difficult. A first step in solving global warming might be to give up driving cars. Giving up cars is not going to be easy. Cars are everywhere, and most of us drive every day. Over the past fifty years countries like the United States, Canada, and Australia have rebuilt themselves around the automobile. It's hard to get anywhere today without a car. The results presented in Figure 3-2 suggest that we should at least start to solve global warming by driving less. Reducing cars would reduce emissions a lot, even if it wouldn't reduce them to zero. Predictions about what would happen if we made changes in our lives can help us decide what kinds of changes to make. The formulation of social policies to fight problems like global warming requires us to make predictions like these. Social scientists try to answer questions about how the world will change in the future depending on the policies we put in place today. Regression models help us answer social policy questions like this. Regression models can also be used to predict things like people's incomes and voting behavior. Simple scatter plots may be useful for helping us understand the overall shape of the relationship between two variables, but regression models go much further in enabling us to make concrete predictions.

This chapter focuses on showing how linear regression models can be used to make predictions about the values of dependent variables. First, like any line a regression like has both a slope and an intercept (Section 3.1). Slopes were covered in Chapter 2, but intercepts also add important information about a line. Second, regression slopes and intercepts are both necessary to compute the expected values of a dependent variable (Section 3.2). Expected values can be used to make predictions about the dependent variable. Third, expected values can be used to predict values of the dependent variable even where data for those variables are missing for particular cases (Section 3.3). As might be expected, predictions made within the range of prior experience tend to be better than predictions about things that have never been observed before. An optional section (Section 3.4) shows how regression prediction can be used to compare different groups in society. Finally, this chapter ends with an applied case study of the relationship between the racial makeup of the population and presidential voting patterns in the 2008 election across the 50 states of the United States (Section 3.5). This case study illustrates how regression lines are drawn based on both their slopes and their intercepts, how the expected values of dependent variables are calculated, and how mean levels of variables can depend on the values of other variables. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should be able to use the results of regression models to understand the determinants of real-world outcomes that are of interest to social scientists.

3.1. Slopes and intercepts The most important feature of a regression line is usually its slope. In many situations, however, when we also want to know the value of a regression line when the independent variable equals zero. In scatter plots like Figure 3-2 and Figure 3-3, the independent variable equals zero at the point where the regression line intercepts the dependent variable axis. Intercepts are the places where regression lines cross the dependent variable axis in a scatter plot. Intercepts can provide meaningful information for interpreting a relationship, as in Figure 3-2 and Figure 3-3, but they are also useful in their own right. If you know both the slope of a regression line and its intercept, you can draw the whole line and every point on it. The use of a slope and an intercept to draw a regression line is illustrated in Figure 3-3. Figure 3-3 shows the regression line connecting passenger cars to carbon emissions from Figure 3-2, but the actual data points have been hidden to show just the line. The slope of the line is .0125, meaning that every 100 extra cars corresponds to a 1.25 ton increase in per capita emissions. The intercept is around 3. To keep all the calculations simple, we'll assume it is exactly 3.00. Starting from this regression intercept of 3.00, an additional 100 cars is associated with an increase of 1.25 in carbon emissions. So the first 100 cars result in carbon emissions of 3.00 + 1.25 = 4.25 tons per capita. Adding 100 more cars on top of these results in carbon emissions of 4.25 + 1.25 = 5.50 tons per capita, and so on. Starting from the intercept of 0 cars and 3.00 tons of carbon, we can draw the whole regression line point by point by using the slope.

It takes up much less space to give just the slope and intercept of a regression line than to graph the whole line on a scatter plot. The regression model graphed in Figure 3-2 and Figure 3-3 is summarized in a table in Figure 3-4. In a typical regression table, independent variables are listed in the first column, with the regression coefficients listed in the following column. Regression coefficients are the slopes and intercepts that define regression lines. In Figure 3-4, there is only one regression model (Model 1) and it only has two coefficients (an intercept and a slope). The intercept (3.00) is listed next to an entry called "[Constant]." The intercept is denoted by "[Constant]" in brackets because, although it's included in the variable list, it's not actually a variable. The terms "constant" and "intercept" are used interchangeably by social scientists.

The slope associated with the independent variable "Cars" (0.0125) is listed next to the entry for "Cars." If there were more independent variables, they would be listed in additional rows. Similarly, if there were more regression models, they would be listed in additional columns. Regression tables are especially convenient for reporting the results of several regression models at the same time. In Chapter 2, the percent of Australians who felt unsafe walking alone at night was regressed on state crime rates (Figure 2-2) and personal experiences of violence (Figure 2-4). Instead of using scatter plots, the results of these two regression analyses can be summarized compactly in a single table, as shown in Figure 3-5. All of the coefficients associated with both models are reported in this one table.

The table in Figure 3-5 shows that in Figure 2-2 the intercept was 8.34 and the slope was 3.20, while in Figure 2-4 the intercept was 3.39 and the slope was 1.37. With just this information, it would be possible to draw the regression lines from the two figures. This information also contains most of the important facts about the two regression lines. For example, we know that even if crime rates were zero in a given state, we would still expect 8.34% of the people in that state to feel unsafe walking alone at night. Similarly, even if no one in a state ever experienced violence personally, we would still expect 3.39% of the people in that state to feel unsafe walking alone at night. Since both slopes are positive, we know that both actual crime and people's experiences of violence make them feel more unsafe when they go out alone at night. To see the regression error and outliers associated with these two regression models we would need scatter plots, but the table of coefficients gives us the basics of the models themselves.

3.2. Calculating expected values Tables of regression coefficients that include slopes and intercepts can also be used to compute the expected values. This should not be surprising, since slopes and intercepts are used to plot regression lines and expected values are just the values on the regression line. Returning to the relationship between passenger cars and carbon dioxide emissions, the slope is 0.0125 and the intercept is 3.00 (Figure 3-4). The slope and intercept define the regression line: the line starts at 3.00 tons of carbon emissions when the number of cars equals 0, then goes up by 0.0125 tons for every 1 additional car. An increase of 0.0125 for every car is the same as 125 for every 100 cars (Figure 3-5). As shown in Figure 3-3, the expected value of carbon emissions for 0 cars is 3.00 tons. For 100 cars the expected value is 4.25 tons. For 200 cars it is 5.50 tons. And so on. Reading expected values off a chart like Figure 3-2 or Figure 3-3 is one way to find them, but a better way is to use the slope and intercept in an equation to compute them. For example, the equation to compute expected values of carbon emissions is depicted in Figure 3-6. This equation uses the slope and intercept for carbon emissions that were reported in Figure 3-4. These are the same slope and intercept that were also used in the scatter plots of carbon emissions versus passenger cars.

Figure 3-6. Equation to compute the expected values of carbon dioxide (CO2) emissions (from Figure 3-4)

Using this equation, it is possible to calculate the expected value of carbon emissions for any level of passenger cars. For example, the level of passenger cars in the United States is 461 cars per 1000 people. Using the equation presented in Figure 3-6, the expected value of carbon dioxide emissions in the United states = 3.00 + 0.0125 x 461 or 8.7625 metric tons per capita. Rounding off to the nearest decimal place gives an expected value of carbon emissions in the United States of about 8.8 metric tons per capita. The actual value of carbon emissions in the United States, 19.5 metric tons, is obviously much higher than expected. As suggested above, this is because nearly half of all Americans drive SUVs and trucks, not cars.

3.3. Predicted values Another use of regression coefficients is to predict levels of the dependent variable for cases that were not included in the regression analysis. Predicted values are expected values of a dependent variable that correspond to selected values of the independent variable. In other words, we can use the equation of a regression line to make predictions. For example, Canada was not included in the carbon dioxide analyses in this chapter because the WDI database (Figure 3-1) was missing passenger car data for Canada. Even though passenger car data for Canada are not available from the WDI, they are available from the Canadian government. According to official Canadian government statistics, there were 290 passenger cars per 1000 people in Canada in 2005. This figure is so low because like Americans almost half of all Canadians drive trucks and SUVs instead of cars. The equation of the regression line for carbon dioxide emissions says that expected carbon dioxide emissions = 3.00 + 0.0125 x passenger cars (Figure 3-6). Using the Canadian government data for passenger cars in Canada, 3.00 + 0.0125 x 290 = 6.625, which rounds off to about 6.6 tons. The actual value for carbon emissions for Canada was 16.6 tons. These figures are graphed in Figure 3-7. Like the United States, Canada has much higher carbon emissions than would be expected based on the regression model.

Predicted values and expected values are very similar concepts. In fact, many people use the two terms to mean the same thing. The difference between them is really just a difference in intentions. The regression line plots the expected values of the dependent variable based on the actual observations of the independent variable. Predicted values are expected values that are used to make predictions about cases for which data do not exist. For example, in Chapter 1 when we were using state median income to study soft drink consumption across the United States we were missing soft drink data for Alaska and Hawaii. Both Alaska and Hawaii were missing data for the dependent variable. Data for the independent variable, state median income, are available for both states: $60,945 for Alaska and $65,146 for Hawaii. These income data can be combined with a regression model using data from the rest of the United States to predict soft drink consumption in Alaska and Hawaii. Figure 3-8 reports the results of a regression model with state median income as the independent variable and state per capita soft drink consumption as the dependent variable. The regression line in this model has an intercept of 93.9 and a slope of -0.60. This means that every $1000 of additional income is associated with a decline of 0.60 gallons in the amount of soft drinks consumed. This regression line is the line that appears on the scatter plot in Figure 1-2. The equation for this line is Soft drink consumption = 93.9 - 0.60 x State median income in thousands of dollars.

Figure 3-8. Table of regression results for the regression of soft drink consumption on state median income (from Figure 1-2)

This equation can be used to calculate predicted values for soft drink consumption in Alaska and Hawaii. Alaska's state median income is approximately $61,000 (rounding off to the nearest thousand to simplify the calculations). The level of soft drink consumption in Alaska predicted by the regression model is 93.9 - 0.60 x 61 = 57.3 gallons. Hawaii's state median income is approximately $65,000 (again rounding to the nearest thousand). Going through the same process for Hawaii gives a predicted value of 93.9 - 0.60 x 65 = 54.9 gallons. The predicted values of soft drink consumption are depicted on the scatter plot of state income and soft drink consumption for the other 48 states and the District of Columbia in Figure 3-9. Alaska and Hawaii may not have exactly the levels of soft drink consumption plotted in Figure 3-9, but these predicted values are the best guesses we can make based on the data we have. They are predictions of how many gallons of soft drinks Alaskans and Hawaiians would be found to drink, if we had the data.

Predicted values can be computed in two different situations. They can be either be calculated for values that fall inside the range of the observed data or for values that fall outside the range of the observed data. Interpolation is the process of using a regression model to compute predicted values inside the range of the observed data. All of the predicted values calculated above -- carbon emissions in Canada, soft drinks in Alaska, and soft drinks in Hawaii -- are examples of interpolation. In all three cases, the values of the dependent variables were within the ranges of values that had already been observed for other cases in the analyses. Sometimes, however, we want to make predictions outside of the values that have already been observed. Extrapolation is the process of using a regression model to compute predicted values outside the range of the observed data. For example, predicting how much carbon emissions there would be in a world with no passenger cars requires extrapolation. There are no countries in the world today that don't have passenger cars. Even Niger in west Africa has 4 passenger cars per 1000 people. Social scientists are usually comfortable with interpolation but cautious about extrapolation. This is because the interpolation of predicted values is based on actual experiences that exist in the real world, but extrapolation is not. For example, we may not know Alaska and Hawaii's levels of soft drink consumption, but we do know the levels of other states with similar income levels. This information can be used to predict Alaska and Hawaii's levels with some confidence. On the other hand, we might hesitate to use the data graphed in Figure 3-9 to predict Puerto Rico's soft drink consumption. Puerto Rico's median income is only $18,610. This is far outside the range of the available data. Using the equation of the regression line from Figure 3-10 to predict Puerto Rico's soft drink consumption would give a predicted value of about 82.7 gallons per capita, but most social scientists would not feel confident making such a prediction.

3.4. Comparing populations using predicted values (optional/advanced) In America, on average, women make less money than men and blacks make less money than whites. According to data on Americans aged 20-29 from the 2008 Survey of Income and Program Participation (SIPP), women earned $4966 less than men and blacks earned $6656 less than whites (on average). These figures are based on a random sample of 4964 full-time employed American twentysomethings in 2008. The data come from Wave 2 of the 2008 SIPP. Income here is defined as wage income (income earned through working a job, as opposed to making money through investments) and is calculated as twelve times the monthly income recorded in the SIPP. The gender gap in wage income is large, and the race gap is larger still. These gender and race gaps in wage income may be due to discrimination, or they may be due to other causes. For example, it is possible that the white men who were given the SIPP survey happened to be older than the people in the other groups. If they were older, they would be expected to have higher incomes. The white men may also be different in other ways. They might have more experience, or more education. It is possible that a portion of the gender and race gaps can be explained by the specific characteristics of the particular people in the sample. In order to compare incomes fairly, it's important to compare like with like. Later chapters of this book will discuss how to "control for" confounding influences like age, education, and experience, but predicted values can also do the job in some situations. For example, predicted values can be used to predict what the incomes in each group would be if all the people were the same age. People's incomes definitely rise with age, starting around age 20. Figure 3-10 reports the results of four regression models using age as the independent variable and wage income as the dependent variable: one for black females, one for black males, one for white females, and one for white males. Note that the intercepts are not very meaningful here. The intercept is the expected value of the dependent variable when the independent variable equals zero. In Figure 3-10, the intercept would represent people's expected wage incomes at age 0. Obviously, that's not a very meaningful concept. It's also an extreme extrapolation from the range of the observed data, which are based on people ages 10-29. In short, the intercepts in Figure 3-10 are just the places where the regression lines start from. They don't have any real meaning beyond that.

Figure 3-10. Table of regression results for the regression of wage income on age for employed SIPP subjects aged 21-30, by race and gender, 2008

The slopes of the regression models reported in Figure 3-10 contrast the effects of an extra year of age on peoples' wage incomes for different groups of people. For black women, every additional year age yields, on average, an extra $1421 of wage income. Black men don't get quite as much advantage from getting a year older, just $1281. The big difference comes with white women and men. For white women, each year of age yields on average an extra $2076 of wage income. The benefits of age for white men are even greater. For white men, every year of age yields on average an extra $2830 of wage income. The expected payoff of an extra year's age for a white man is nearly twice as high as the average payoff for a black woman. The coefficients of the for regression models reported in Figure 3-10 can be used to calculate predicted values for the wage incomes of black females, black males, white females, and white males at any given age. From Figure 3-10, the regression model for black women was Wage income = -7767 + 1421 x Age. For black women of various ages, this works out to: Age 25: Wage income = -7767 + 1421 x 25 =$27,758 Age 30: Wage income = -7767 + 1421 x 30 =$34,863 Age 40: Wage income = -7767 + 1421 x 40 =$49,073 These figures are reported in Figure 3-11 in the column for black females. Figures for black men, white women, and white men are calculated in the same way. The prediction of wage income at age 25 for each group is an interpolation, since the ages of the SIPP participants in the study were 20-29. As an interpolation, it should be a pretty accurate estimate of the incomes of 25-year-olds in each category would be expected to earn. The prediction of wage income at age 30 is on the very edge between an interpolation and an extrapolation, so it might be less reliable. The prediction of wage income at age 40 is an extrapolation far out into the future, so far that most social scientists would not trust it at all. The age 40 extrapolation is included here just to illustrate how extrapolation works.

What do the models tell us about discrimination? In the SIPP data overall, the income gap between women and men in their twenties is $4966, while the income gap between blacks and whites is $6656. Comparing the predicted incomes of people at age 25, the predicted income for black women is $3082 less than that for black men, while the predicted income for white women is $3994 less than that for white men. This means that taking into account race and experience, 25-year-old women earn something like $3000-$4000 less than men, not close to $5000 as indicated by the raw data. Similarly, the predicted income at age 25 for black women is $4855 less than that for white women, while the predicted income for black men is $5757 less than that for white men. Again, the differences adjusted for age and sex are large, but not as large as raw race gap of $6656. At age 25, the gender and race gaps in wage income are large, but not as large as might have been thought based just on the raw data.

3.5. Case study: Predicting state election outcomes based on race On November 4, 2008, Barack Obama was elected the first black President of the United States. President Obama's father was Kenyan and Barack Obama himself grew up mainly in Hawaii, far from the historical center of American civil rights struggles. Nonetheless, like any black American Obama would have been affected by racial discrimination throughout his life. Both Obama and America overcame racial discrimination when Obama was elected President, but was his race a factor in his election? Regression models can help shed light on the role played by race in the 2008 election. Most of the time discrimination hurts a person, but sometimes it can also help a person. In the 2008 presidential election, black Americans voted overwhelmingly for Barack Obama. According to CNN news, exit polls on election night indicated that 96% of blacks voted for Obama. These votes certainly helped Obama win the election, but American elections aren't determined just by the number of people who vote for a candidate. They are determined by state electoral votes. In most states, whoever receives the most votes within the state gets all of that state's electoral votes. Thus, it is possible to win the most votes but still lose the election. This happened to Al Gore in 2000, when he won more people's votes than George Bush but fewer state electoral votes. In the 2008 election, Obama won both the most people's votes and the most state electoral votes, and so was elected President. Strangely, though, he lost the election in some of the states that have the highest black populations. For example, Mississippi has the highest percentage of blacks of any state in the United States (37.2% black), but Obama received only 43.0% of the vote in Mississippi and lost the state to his opponent, John McCain. The same thing happened in other heavily black states, like Alabama and Louisiana. The relationship between the percent of a state's population that is black and the percent of a state's voters who voted for Obama is plotted in Figure 3-12. It turns out that there was almost no relationship between a state's black population and its presidential vote in 2008. The slope of the regression line is actually slightly negative. This means that states with higher black populations tended to vote slightly less for Obama. The highest vote for Obama was in the state where he grew up, Hawaii (71.9%). The very lowest vote for Obama was in the historically Republican western states of Wyoming (32.5%).

How is it possible that there was no relationship between the number of blacks in a state and the vote for Obama in that state, given that 96% of black Americans voted for Barack Obama? The answer is that in many states with large numbers of blacks, whites voted overwhelmingly for his opponent, John McCain. This trend was particularly pronounced in the South. The historical center of the struggle for civil rights for black Americans has always been the South, in particular the 11 states of the former Confederacy that seceded from the United States during the Civil War (1861-1865). The 11 Confederate states were strongly committed to continuing the institution of slavery, and after being readmitted to the Union they put in place policies and laws that discriminated heavily against their black citizens. Black Americans have suffered discrimination everywhere in the United States, but the levels of discrimination in the 11 former Confederate states have historically been much worse than elsewhere. Figure 3-13 plots exactly the same data as Figure 3-12, but divides the states into the 39 "free" states that were never part of the Confederacy versus the 11 former Confederate states that seceded from the United States during the Civil War. The free states are marked with diamonds and the former Confederate states are marked with X's. Separate regression lines have been plotted for the two groups of states. Among the 39 free states, states with higher black populations returned higher votes for Obama, as would be expected. Among the 11 former Confederate states, states with higher black populations actually returned lower votes for Obama.

Figure 3-14 summarizes the regression coefficients for the lines plotted in Figure 3-12 and Figure 3-13. The line plotted in Figure 3-12 for all states is Model 1 in Figure 3-14. The free state line plotted in Figure 3-13 is Model 2 and the former Confederate state line plotted in Figure 3-13 is Model 3. The number of cases (N) for each model has been noted in the table. In Model 1, the intercept is 51.1 and the slope is -0.057. The intercept of 51.1 means that the predicted value of the Obama vote for a state with no black voters would be 51.1%. This is an extrapolation, since there are no states that actually have 0% black populations. In general, extrapolations are less reliable than interpolations, but in this case the extrapolation is very slight, since several states have black populations under 1%.

The slope in Model 1 is -0.057. This means that for every 1% rise in a state's black population, the Obama vote would be expected to fall by 0.057%. This is a very, very slight downward slope. The number of blacks in a state has essentially no effect on that state's total vote for Obama. Excluding the former Confederate states, the free states model (Model 2) has an intercept of 48.1. This means that Model 2 would predict a vote for Obama of 48.1% in a state that had no black voters. This is different from the prediction of Model 1, but not very different. Both predictions (51.1% from Model 1 and 48.1% from Model 2) are within the range of actual votes for Obama in states that have very small numbers of black voters, like Vermont and Wyoming. More interesting is the slope of Model 2. Focusing on just the 39 free states, the slope of the regression line is clearly positive. For the 39 free states, every 1% rise in a state's black population is associated with a 0.576% increase in the vote for Obama. This is a large effect. An increase of one point in the black population predicts an increase of half a point in the vote for Obama. Model 3 repeats the regression of the Obama vote on state percent black, but this time using only the 11 Southern states that were historically part of the Confederacy that seceded from the United States during the Civil War (1861-1865). Among the former Confederate states, the predicted value of the vote for Obama in a state with no black voters would be 47.3. This prediction is an extrapolation far outside the observed range of the numbers of black voters in these states, but it is still a credible figure. It is a little lower than the equivalent predictions from Model 1 and Model 2, but not much lower, and it is within the range of actually observed votes for Obama in the free states with small black populations. The more important coefficient in Model 3 is the slope. The slope is -0.114. This means that among the 11 former Confederate states, an increase of 1% in the percent of the population that is black is associated with a decline of 0.114% in the vote for Obama. Each one point increase in the black population predicts a decline of just over a tenth of a point in the vote for Obama. This is striking. Outside the South, the more blacks there were in a state, the more people voted for Obama. In the South, the more blacks there were in a state, the more people voted for McCain. High votes for John McCain are not evidence of racism. There is no reason to think that a 67.5% vote for McCain in Wyoming is evidence of racism in Wyoming. But in the states that have the worst history of racism -- and only in those states -- the vote for John McCain was strongest in the states that had the most black citizens. In other words, Southern whites were more likely to vote for McCain if they had black neighbors. If there were fewer blacks in a state, whites were more comfortable voting for Obama, but if there were more blacks in a state, whites tended to vote for McCain. This is very strong circumstantial evidence of a legacy of racism in those states. Further research would be necessary to more fully understand these voting patterns, but the regression models reported in Figure 3-14 do raise serious questions about race and racism in America today.

Chapter 3 Key Terms

Extrapolation is the process of using a regression model to compute predicted values inside the range of the observed data.
Intercepts are the places where regression lines cross the dependent variable axis in a scatter plot.
Interpolation is the process of using a regression model to compute predicted values inside the range of the observed data.
Predicted values are expected values of a dependent variable that correspond to selected values of the independent variable.
Regression coefficients are the slopes and intercepts that define regression lines.

Means and Standard Deviations

North Americans, Europeans, Japanese, Australians, Koreans, and New Zealanders, and people in a few other countries are very lucky. However difficult life may be for individual people, our countries are very rich. If we in the rich world have problems like poverty, homelessness, and malnutrition, it's because we choose to have them. We could always just decide to spend the money to make sure that everyone could live a decent life. We may choose not to spend the money, but at least we have the choice. National income per person in the rich countries of the world is typically $30,000 - $45,000 per person per year, and all of the rich countries of the world have democratic governments. It's up to us to decide how we want to spend our resources. In many of the poorer countries of the world, the resources simply do not exist to make sure that everyone has a decent standard of living. What's worse, many of these countries aren't democracies, so even where resources do exist people don't necessarily have the power to choose to share them out equally. As a result, over one-third of the world's children under age 5 are stunted (shorter than they should be) due to malnutrition. Over 20% of the world's population can't afford to eat on a regular basis. About 40% of the people of the world -- roughly 2.5 billion people -- when they have to go to the bathroom literally shit on the ground. Another 30% use outhouses. Only about 30% of the world's people have toilets with running water. It's hard to wash after you wipe if there's no running water in your bathroom. Most rich countries make some effort to help make conditions better for the world's poor. Some basic data on rich countries' overseas development assistance (ODA) budgets are presented in Figure 4-1. Overseas development assistance is the amount a country spends on aid to help people in poorer countries. This database draws together data from the World Bank and the Organization for Economic Cooperation and Development (OECD). The cases in the database are 20 of the richest countries in the world, including the United States. Included are two metadata items, the countries' names and three-digit country codes. Four variables are also included: AID/GNP -- a country's ODA spending in relationship to its total national income ADMIN/AID -- the proportion of a country's aid that is spent on administrative costs MIL/GNP -- a country's military spending in relationship to its national income GDP_2008 -- a country's level of national income per capita EUROPEAN -- an indicator that a country is European (1) versus non-European (0)

The twenty rich countries included in Figure 4-1 are ranked by the generosity of their ODA spending in Figure 4-2. Compared to other rich countries, the United States comes in dead last. The United States spends less on aid (as a proportion of its total income) than any other country, 0.19%. Other countries are more generous, but not much more generous. Australia and Canada give 34 cents of every $100. France and Germany give 40 cents. Norway, Luxembourg, and Sweden are the most generous, giving about 1% of their total national incomes to help others. To match the most generous countries in the world, the United States would have to quintuple its annual ODA spending.

An interesting pattern in ODA spending that is made clear by Figure 4-2 is that all of the most generous countries are European. We might generalize from this observation to hypothesize that European country status is an important determinant of ODA spending levels. The results of a regression of ODA spending on European country status are reported in Figure 4-3. The intercept is 0.27, which is the expected value of ODA spending when European status = 0. In other words, rich non-European countries tend to give about 0.27% of their national incomes. The regression coefficients in Figure 4-3 can also be used to calculate the expected value of ODA spending for European countries. For European countries, European status = 1, so ODA spending = 0.27 + 0.33 x 1 = 0.60% of national income. This expected value could be used to predict ODA spending in a rich European country that was not included in the database, like Liechtenstein. Based on the regression reported in Figure 4-3 the predicted value of ODA spending for Liechtenstein would be 0.60% of national income. Since Liechtenstein is a European country (European status = 1), this prediction would be an interpolation, not an extrapolation.

A scatter plot of the relationship between European country status and ODA spending is depicted in Figure 4-4. A regression line has been plotted on the graph. The expected values of ODA spending for both non-European and European countries have also been noted. As with any regression model, the regression line graphed in Figure 4-4 passes through the middle of the scatter of the data. The only thing that is different from the scatter plots in Chapter 1 and Chapter 2 is that the independent variable in Figure 4-4 takes only two values. As a result, all the points line up over either European status = 0 or European status = 1. This has no effect on the meaning of the regression line or how it is calculated. The line still represents the most likely value of the dependent variable (ODA spending) for any given level of the independent variable (European country status). Similarly, deviations from the regression line still represent error.

This chapter explains how expected values and errors can be used to describe and compare variables. First, even one variable alone can have an expected value, without any need for a linear regression model (Section 4.1). A new model, the means model, is introduced to define the expected value of a variable when there are no other variables involved in the analysis. Second, any expected value is associated with error, since in most cases the values of variables don't equal their expected values (Section 4.2). In both mean models and regression models the errors balance each other out and average out to zero. Third, in both mean models and regression models the amount of error can be measured using a standard deviation (Section 4.3). Most of the data used in a statistical model fall within the standard deviation of the error. An optional section (Section 4.4) demonstrates how standard deviations are actually calculated by statistical computer programs. Finally, this chapter ends with an applied case study of income and employment levels across the 33 political divisions of China (Section 4.5). This case study illustrates how means can be used to compare variables. It also shows how regression standard deviations are related to the standard deviations of variables. All of this chapter's key concepts are used in this case study. By the end of this chapter, should have gained a much deeper understanding of the role played by error in statistical models.

4.1. The mean model As Figure 4.4 demonstrates, a regression model can be used to calculate the expected value of Overseas Development Assistance (ODA) either for non-European countries or for European countries. The expected value of a dependent variable for a specific group of cases (like non-European or European countries) is known as a conditional mean. Conditional means are the expected values of dependent variables for specific groups of cases. Another example of the use of conditional means is illustrated in Figure 4-5. Figure 4-5 depicts a scatter plot and regression of wage income on gender using data for employed Americans aged 20-29 from the 2008 US Survey of Income and Program Participation (SIPP), Wave 2. The SIPP database includes 4964 cases (2208 women and 2756 men). Since these would be too many to plot on a scatter plot, 100 random cases (46 women and 54 men) have been graphed in Figure 4-5 to illustrate what the data look like.

The coefficients of the regression of income on gender are reported in Figure 4-6. In this regression model, the independent variable is gender (coded as "maleness": 0 for women and 1 for men) and the dependent variable is wage income (defined as income earned through working a job and calculated as twelve times the monthly income recorded in the SIPP). The regression model has an intercept of 33876 and a slope of 4866. In other words, the equation for the regression line is Income = 33876 + 4966 x Male. For women (Male = 0), the expected value of wage income is 33876 + 4966 x 0 = 33876 + 0 = $33,876. For men (Male = 1), the expected value of wage income is 33876 + 4966 x 1 = 33876 + 4966 = $38,842. In other words, the conditional mean income for women is $33,876 while the conditional mean income for men is $38,842.

If it's possible to calculate conditional mean incomes based on people's genders, it should be possible to calculate the mean income for people for people in general. Means are the expected values of variables. What would happen if we put all 4964 people in the SIPP database together into one big group and calculated the expected value of their income? The result would look something like Figure 4-7, which takes the 46 women and 54 men from Figure 4-5 and groups them into a single category called "people."

The mean income of all 4964 employed Americans age 20-29 is $36,633. The mean income can be calculated by adding up the incomes of all 4964 people and dividing by 4964. This is what most people would call the "average" value of a variable. Social scientists usually use the term "mean" instead of the term "average" because "average" can also mean "typical" or "ordinary." The term "mean" always means just one thing: it is the expected value of a variable, calculated by summing up the values of all the individual cases of a variable and dividing by the number of cases. The mean is more than just a mathematical calculation. Like the mean income of $36,633 for all twentysomethings, the mean incomes for women ($33,876) and for men ($38,842) could have been calculated by summing up all the incomes of the women or men in the database and dividing by the number of women or men. The conditional means of income for women and men from the regression model in Figure 4-6 are identical to the individual means of income for women and men. The difference is that calculating the conditional means using a regression model provided both an equation and a statistical model for thinking of the conditional means as predicted values. Based on the regression model for income (Figure 4-6), any employed twentysomething American woman would be predicted to have an income of $33,876. Any employed twentysomething American man would be predicted to have an income of $38,842. What would be the predicted income of an employed twentysomething American in general, if the SIPP database had included no information on gender? Obviously, the answer would be $36,633, the mean income for all 4964 people in the database. The statistical model behind this prediction is a mean model. Mean models are very simple statistical models in which a variable has just one expected value, its mean. The mean model can be thought of as a linear regression model with no independent variable. If you squeeze all the data from Figure 4-5 into a single group like in Figure 4-7, you turn a linear regression model into a mean model. The big difference between using a mean model as a statistical model and just calculating a mean by adding up all the values and dividing by the number of cases is how you think about it. In the mean model, the mean is an expected value, not just a bunch of arithmetic. Each time an individual case deviates from the mean, that deviation is a form of error. In a linear regression model, regression error is the degree to which an expected value of a dependent variable differs from its actual value. In the mean model, error is the degree to which the mean of a variable differs from its actual value. In the mean model, if a person earns $30,000 per year, that income can be divided into two parts: the mean income ($36,633) and error ($6633). If another person earns $40,000 a year, that income can be divided into two parts: the mean income ($36,633) and error ($3367). In the mean model, your income isn't just your income. Your income is composed of the mean income for a person like you, plus or minus some error.

4.2. Models, parameters, and degrees of freedom Smoking causes more preventable disability and death worldwide than any other human activity. It is an incredibly important challenge to the world's health. In Canada, about 17.9% of the adult population identify themselves as smokers (Health Canada data for 2008). Smoking rates, heavy drinking rates, and temperatures across the 13 Canadian provinces and territories are summarized in the database in Figure 4-8. The mean rate of smoking across these 13 political divisions is 20.3%. This differs from the overall national average because several low-population provinces and territories have high smoking rates. A mean model for smoking rates in Canadian provinces and territories would suggest that smoking rates equal an expected value of 20.3% plus or minus some error in each case.

The mean model is a very simple approach to understanding smoking rates. It says something about smoking rates -- that they're not 0% or 50% -- but doesn't say anything about why smoking rates differ from province to province. All the variability in smoking rates across provinces is considered to be error in the model. A regression model might help explain some of the differences in smoking rates across Canada's 13 provinces and territories. One theory of the differences in smoking rates might be that smoking rates depend on the weather. Canada is cold. The mean annual temperature across the capital cities of Canada's 13 provinces and territories is less 38 degrees Fahrenheit. This is much colder than New York (57 degrees), Chicago (51 degrees), or Los Angeles (66 degrees). Even Minneapolis (average annual temperature 45 degrees) and Fargo (41 degrees) are warmer than most of Canada. One theory might be that some people smoke because they get bored when they can't go out in the cold weather. A specific hypothesis based on this theory would be that smoking rates rise as the average temperature falls. The results of a regression model using average annual temperature as the independent variable and the smoking rate as the dependent variable are presented in Figure 4-9.

The intercept of 37.00 means that a province with an annual average temperature of 0 degrees would have an expected smoking rate of 37.0%. Since none of Canada's provinces is this cold, the intercept is an extrapolation. Starting at the intercept of 37.0%, the expected value of the smoking rate declines by 0.44% for every 1 degree increase in temperature. As predicted by the boredom theory of smoking, smoking rates fall as the temperature rises. Which model is better for understanding smoking rates, the mean model or the linear regression model? Both provide expected values. The relationship between the mean model and the regression model for smoking is graphed in Figure 4-10. The left side of Figure 4-10 depicts the mean model for smoking, lining up all the provinces just like the SIPP respondents in Figure 4-7. The right side of Figure 4-10 depicts the regression model for smoking, spreading the provinces out according to their temperatures. Arrows show how the data points in the mean model correspond to the data points in the regression model for four illustrative provinces. In the case of smoking in Canadian provinces, the regression model seems to explain more about smoking than the mean model. Given the availability of temperature data, the regression model seems more useful than the mean model.

The mean model in Figure 4-10 gives an expected value for the overall level of smoking using just one figure (the mean) while the regression model gives different expected values of smoking for each province using two figures (the intercept and the slope). These figures are called parameters. Parameters are the figures associated with statistical models, like means and regression coefficients. Calculating parameters like means and regression coefficients require data. In the Canadian province data (Figure 4-8) there's plenty of data to calculate both the mean and the regression coefficients. Usually it's not a problem to have enough data to calculate the parameters of a model, but when there are very few data points there can be problems. What if you had a database with just one case? For example, you might want to study the population of the world in 2010. The population of the world is around 6.7 billion people. Can you model the population of the world using a mean model? Yes, the population of the world in 2010 has a mean of 6.7 billion people. There's no error in this mean model, because there's only one case -- the world -- and its actual population is equal to the mean. With a database of 1 case, it is possible to calculate the 1 parameter of the mean model, the mean. Could you study the population of the world in 2010 using a linear regression model? You might hypothesize that population is related to rainfall. If the world were all one big dry desert, it would be expected to have a small population. If the world were all a lush green paradise, it would be expected to have a large population. This is a good idea, but the problem is that there is only one world to study. It is impossible to calculate the affect of rainfall on the population of the world when there is only one world to study. Regression models require the calculation of two parameters, and it turns out that you have to have a database of at least two cases in order to calculate both a slope and an intercept. What if you had a database with two cases? For example, you might want to model Korean populations. There are two Korean countries, North Korea and South Korea. North Korea has a population of 24 million people, while South Korea has a population of 48 million. Using the mean model, the expected value of the population of a Korean country is the mean of these two cases, or 36 million people. Both North Korea and South Korea have an error of 12 million (North Korea has 12 million less people than the mean, while South Korea has 12 million more than the mean). Even though it seems like both cases have independent errors, in fact there is only one level of error in the model. If North Korea is 12 million below the mean, South Korea has to be 12 million above the mean to balance it out. There are two errors, but only one of them is free to vary. This quirky mathematical fact means that in the mean model, every case isn't free to vary at random. If a variable has 2 cases, and you know the mean of the variable, then only 1 case can vary freely. The other case has to balance out the first case. If there are three cases, then only two can vary freely. More generally, if there are N cases, and you know the mean, only N-1 cases are free to vary. This number, N-1, is knows as the degrees of freedom of a mean model. Degrees of freedom are the number of errors in a model that are actually free to vary. The degrees of freedom of a mean model is N-1 because the mean model has only one parameter, the mean. On the other hand, the degrees of freedom of a regression model is N-2, because the regression model has two parameters (the slope and intercept). That means that there have to be at least two cases in a database in order to use a regression model. Since most databases have dozens or hundreds of cases, this usually isn't a problem. The main use of degrees of freedom is in making statistical calculations about error. The total amount of error in a statistical model depends on the total number of degrees of freedom, not on the total number of cases. Statistical computer programs use degrees of freedom in calculating many of the figures associated with statistical models, and usually report the degrees of freedom of the model as part of their output of model results. The basic idea, though, is just that any statistical model uses up one degree of freedom for every parameter it calculates. A mean model with 1 parameter based on N cases has N-1 degree of freedom. A linear regression model with 2 parameters has N-2 degrees of freedom. No model can have negative degrees of freedom, so it takes at least 1 case to use a mean model and 2 cases to use a regression model.

4.3. Standard deviation and regression error All statistical models that use parameters to produce expected values (like the mean model and the linear regression model) produce model error. All this means is that statistical models usually describe the world perfectly well. All statistical models are simplifications of the real world, so they all have error. The error in a mean model is usually just called error or deviation from the mean, while the error in a regression model is usually called regression error. In the mean model, the model explains none of the variability in the variable. The mean model has only one parameter, the mean, and all of the variability in the variable becomes error in the mean model. As a result, the spread of values of the error is just as wide as the spread of values of the variable itself. This spread can be measured and expressed as a number. The most commonly used measure of the spread of a variable is the standard deviation. Standard deviation is a measure of the amount of spread in a variable, which is the same thing as the amount of spread in the error in a mean model. The standard deviation of a variable (or the standard deviation of the error in a mean model) depends on two things: the amount of error in the mean model and the number of degrees of freedom in the mean model. For the smoking rates of the 13 Canadian provinces and territories, the standard deviation is 5.3%. In the linear regression model, some portion of the variability in the dependent variable is accounted for by variation in the independent variable. This is illustrated in Figure 4-10, where the smoking rates of the 13 Canadian provinces and territories are spread out over the levels of their average annual temperatures. If you look carefully at Figure 4-10, you'll see that the regression errors (the differences between the expected values on the regression line and the actual values of smoking rates on the right side of the chart) look pretty small compared to the overall variation in smoking rates (from the left side of the chart). Part of the variation in smoking goes into the regression line and part of the variability in smoking goes into error. As a result of this, the overall level of error in a regression model is always smaller than the overall level of error in the corresponding mean model. Errors from both kinds of model are directly compared in Figure 4-11 for the Canadian provincial smoking data. The table in Figure 4-11 shows the expected values and associated errors for each province for the mean model and for the regression model. The expected value in the mean model is always 20.3% (the mean). The expected value for each province in the regression model is calculated from the equation for the regression of smoking on temperature (Figure 4-9). As the table in Figure 4-11 shows, the errors in the regression model are usually smaller in size than the errors in the mean model. The difference is biggest for the provinces with the biggest errors. The largest error in the regression model is 5.8% (Yukon). Four different provinces (including Yukon) have errors larger then 5.8% in the mean model.

The standard deviation of the model error in the regression model is 3.1%. This is called regression model standard deviation. Regression error standard deviation is a measure of the amount of spread in the error in a regression model. Regression error standard deviation is based on the errors in the regression model and the degrees of freedom of the regression model. Regression error standard deviation for a given regression model is almost always smaller than the standard deviation from the corresponding mean model. In fact, the coefficients of regression models (slopes and intercepts) are selected in such a way as the produce the lowest possible regression error standard deviation. Standard deviations measure the spread of the error in a model. A higher standard deviation means more error. Figure 4-12 illustrates the spread of the error for the mean model and regression model for Canadian provincial smoking rates. The error figures plotted in Figure 4-12 are taken directly from the two error columns in Figure 4-11. Some of the provinces and territories with the largest errors are marked on the chart. In each model, the errors of most of the provinces and territories fall within one standard deviation of zero. The error standard deviation of the mean model is 5.3%, and 9 out of 13 provinces fall between +5.3% and -5.3%. All 13 provinces fall within two standard deviations (between +10.6% and -10.6%). Figure 4-12. Illustration of standard deviation and regression error standard deviation for mean and regression models of smoking rates across the 13 Canadian provinces and territories, 2008

For the regression model, the error standard deviation is smaller, but still 9 out of 13 provinces fall within one standard deviation of their expected values, with errors ranging between +3.1% and -3.1%. Again, all 13 provinces have model errors that fall within two standard deviations (+6.2% to -6.2%). There is no rule that errors must fall within two standard deviations, but usually they do. Usually model results look something like Figure 4-12, with most expected values falling within one standard deviation of their observed values (error less than one standard deviation) and the vast majority of expected values falling within two standard deviations of their observed values (error less than two standard deviations). When a model has a small error standard deviation, that means that the model produces good, accurate estimates of the dependent variable.

4.4. Calculating variance and standard deviation (optional/advanced) There is rarely any need to calculate the variance and standard deviation of a variable or of the error in a mean model or linear regression model. Statistical computer programs, spreadsheet programs, and even calculators all are able to calculate standard deviation. On the other hand, unlike calculating regression coefficients, calculating standard deviation is not too difficult. There are six steps in the calculation of the standard deviation of a variable. They are: (1) Calculate the mean of the variable (2) Calculate deviations from the mean for each case of the variable (3) Square these deviations (4) Sum up all the deviations into total squared deviation (5) Divide total squared deviation by the degrees of freedom to arrive at variance (6) Take the square root of variance to arrive at standard deviation These six steps in the calculation of standard deviation are illustrated in Figure 4-13 using data on the number of subway stations in each borough of New York City. Including the 22 stations of the Staten Island Railway as subway stations, there are a total of 490 stations in the five boroughs. Dividing 490 by 5 gives a mean number of subway stations per borough of 98 (Step 1). Each borough's deviation from this mean of 98 stations is given in the table (Step 2). To the right of the deviations are the deviations squared (Step 3). The sum total of these squared deviations is 14434 (Step 4). Since there are five boroughs, and the deviations in Figure 4-13 are deviations from a mean model (not a regression model), there are 4 degrees of freedom (5 - 1 = 4). Dividing the total squared deviation by the degrees of freedom (14434 / 4) gives the variance of the number of subway stations per borough.

Variance is sometimes used instead of standard deviation as a measure of the spread of a variable. The problem with variance is that it is not very intuitively meaningful. For example, the variance of the number of subway stations in Figure 4-13 is 14434. Since variance is a sum of squared deviations, it is expressed in squared units. As a result, the variance in Figure 4-13 is really 14434 squared stations. Since there's no such thing as a squared station, it makes sense to take the square root of variance. Taking the square root of variance give standard deviation. The standard deviation in Figure 4-13 represents a number of stations. The number of subway stations per borough of New York City has a mean of 98 stations and a standard deviation of 60.1 stations. Calculating regression error standard deviation works exactly the same way as calculating standard deviation, except that the degrees of freedom equal N-2 instead of N-1. This difference in the degrees of freedom is the reason why it is possible (though unlikely) for regression error standard deviation to be greater than the standard deviation from a mean model. The expected values from a regression model are always closer to the observed values of the dependent variable than the expected values from a mean model. This is because the expected values from a regression model vary, while the expected values from a mean model are constant (they're just the mean). Since the regression expected values are closer to the observed values of the dependent variable, their errors (deviations) are smaller, and their squared errors (deviations) are smaller. The degrees of freedom in the regression model, however, are smaller as well (N-2 instead of N-1). It is just possible that the smaller degrees of freedom can offset the smaller squared error to produce a larger variance. As a rule, linear regression models always have less error standard deviation than mean models unless both the slope and the number of cases (N) are very small. When the slope is small, the expected values of the regression model are not very different from the expected values of the mean model: both are constant, or nearly so. When the number of cases is small, the difference in the degrees of freedom can be big enough to matter (the difference between 4 and 3 is much more important than the difference between 4000 and 3999). In practice, this (almost) never happens. Where data are available to calculate expected and predicted values using a regression model, these will (almost) always be better than expected or predicted values from a mean model. A mean model would only be used to make predictions where the data weren't available to use a linear regression model.

4.5. Case study: Income and wage employment in China China has been experiencing extraordinarily rapid rates of economic growth since the late 1990s. Nonetheless, China as a whole is still a relatively poor country. It's average income levels are less than half that of Mexico. One characteristic of poor countries all over the world is that many people live off the land growing their own food instead of working for pay. As incomes rise, more and more people move off the land to seek employment in factories and other workplaces that pay money wages. In China today, millions of people are moving from small farming villages to new urban areas every year, making the transition from subsistence farming to wage labor. Social scientists debate whether people are better off as subsistence farmers or better off as wage laborers, but either way the trend is unmistakable. Millions of Chinese join the ranks of wage laborers every year. Like Canada and Australia, China had more than one kind of administrative division. In China, there are 4 independent municipalities (the biggest cities in the country), 22 provinces, and 5 "autonomous regions" that have large minority populations and have different administrative procedures than regular provinces. There are also two "special administrative regions" (Hong Kong and Macau) that for historical reasons are not included in many Chinese data. In addition, China claims ownership of but does not control the island of Taiwan. All told, most Chinese datasets include variables for the 31 main divisions, excluding Hong Kong, Macau, and Taiwan. A database containing population, income, and employment data for these 31 divisions is reproduced as Figure 4-14.

Two variables in Figure 4-14 are particularly interesting for understanding the transition from subsistence agriculture to wage labor. The variable INC$2008 is the mean income level for wage earners in each administrative division, and the variable EMP(%) is the labor force participation rate (the proportion of people in each division who are employed in formal wage labor). Conditional mean levels of income, conditional on the type of division, are plotted in Figure 4-15. The mean income level in each type of division (municipality, province, or region) is reported on the graph. The four municipalities are much richer than the provinces and regions, but there is one relatively poorer municipality, Chongquing, which is inland deep in the middle of China. There is one apparently rich region, Tibet, but in fact Tibet is relatively poor. The very high cost of living in Tibet keeps wages higher than they otherwise might be.

Figure 4-16 contrasts two models of labor force participation for the 22 Chinese provinces. Figure 4-16 focuses on the provinces because there are more provinces than other divisions and municipalities and regions are different in many ways from provinces. The left side of Figure 4-16 presents a mean model with 21 degrees of freedom for labor force participation (marked LFP). The mean level of labor force participation across the 22 provinces is 54.4%, with a standard deviation of 6.9%. All provinces except Zhijiang have labor force participation rates that fall within two standard deviations of the mean. The right side of Figure 4-16 presents a linear regression model with 20 degrees of freedom that regresses labor force participation (dependent variable) on mean income level (independent variable). The parameters of this model are reported in Figure 4-17.

The regression model slope of 6.3 implies that for every $1000 rise in wage rates, the expected value of the labor force participation rate rises by 6.3%. The regression error standard deviation of this model is 3.4%, which is less than half the mean model standard deviation of 6.9%. The strong positive slope and the low level of error in the regression model suggest that the regression model provides a much better representation of labor force participation than the mean model. Labor force participation in Chinese provinces does seem to rise at least in part in line with rising wage incomes.

Chapter 4 Key Terms

Conditional means are the expected values of dependent variables for specific groups of cases.
Degrees of freedom are the number of errors in a model that are actually free to vary.
Mean models are very simple statistical models in which a variable has just one expected value, its mean.
Means are the expected values of variables.
Parameters are the figures associated with statistical models, like means and regression coefficients.
Regression error standard deviation is a measure of the amount of spread in the error in a regression model.
Standard deviation is a measure of the amount of spread in a variable, which is the same thing as the amount of spread in the error in a mean model.

The Role of Error in Statistical Models

The United States has a long and troubled history of discrimination and repression based on race. Until 1865, slavery was widespread in the United States, with rich white people legally owning, oppressing, and abusing black people. For the next century between 1865 and 1964 the race-based segregation of schools, businesses, and other public places was legal, and in much of the country black Americans were prohibited from fully participating in society. Any American over age 50 today was born in a segregated country that did not give equal rights to its black citizens. It is not surprising that racial discrimination is still a major problem in America despite the election of America's first black President. After all, Barack Obama himself was born in a legally segregated America. One outcome of the long history of racial discrimination in America is a continuing wage gap between blacks and whites. Even blacks born long after the end of official segregation in American earn substantially lower salaries than whites of the same age. The race gap in wages can be illustrated using data from the 2008 US Survey of Income and Program Participation (SIPP). Wave 2 of the 2008 SIPP includes wage income data for 4964 employed Americans aged 20-29 (633 of them black and 4331 of them white). The overall mean income in the SIPP sample is $36,633 with a standard deviation of $29,341. The conditional mean incomes of the 633 blacks and 4331 whites in the SIPP sample are reported in Figure 5-1. The black mean is $6656 lower than the white mean.

In a mean model for black wage income, the expected value of wage income for twentysomething black Americans is $30,826. Observed incomes less than or greater than $30,826 would be error from the standpoint of this model. The standard deviation of the error ($22,723) indicates that there is a wide spread in the actual incomes of black Americans. The expected values of wage income for twentysomething white Americans is $37,482. The standard deviation of the model ($30,096) indicates an even wider spread in incomes for white Americans than for black Americans. The mean model for black Americans uses one parameter (its mean) and is based on 633 cases, so it has 632 degrees of freedom. The mean model for white Americans has 4331 data points and 1 parameter, so it has 4330 degrees of freedom. Both models have plenty of degrees of freedom (anything more than 10 or so is fine). Another way to model the difference in incomes between black and white Americans would be to use a regression model. The coefficients of the regression of income on race are reported in Figure 5-2. In this regression model, the independent variable is race (coded as "blackness": 0 for whites and 1 for blacks) and the dependent variable is wage income. The regression model has an intercept of 37482 and a slope of -6656. In other words, the equation for the regression line is Income = 37482 - 6656 x Black. For whites (Black = 0), the expected value of wage income is 37842 - 6656 x 0 = 37482 + 0 = $37,842. For blacks (Black = 1), the expected value of wage income is 37842 + 6656 x 1 = 33876 - 6656 = $30,826. These expected values from the regression model are identical to the conditional means from the two mean models in Figure 5-1.

The regression model uses all 4964 cases and has 2 parameters, leaving it with 4962 degrees of freedom. The regression error standard deviation in the regression model is $29,263 (regression model standard deviations usually aren't reported in tables of results, but they can be computed using statistical software programs). The slope of the regression line represents the race gap in incomes. The fact that the slope is negative means that the blacks in the SIPP sample reported earning less money than the whites in the SIPP sample. Does this mean that racial discrimination is still going on? That's hard to say. The high regression error standard deviation means that there is a lot of variability in people's incomes that is not captured by the regression model. The observed race gap of $6656 seems pretty big, but further analysis will be needed to determine whether or not it truly represents real racial differences in American society.

This chapter introduces the concept of statistical inference in the context of mean and regression models. First, inferential statistics are used to make conclusions about the social world as a whole (Section 5.1). This contrasts with descriptive statistics, which merely describe the data that are actually observed and recorded in databases. Second, all inferential statistics are based on the idea that the model error represented in the observed data are a random sample from all the errors that could have happened in the real world (Section 5.2). Different kinds of non-random sampling have different effects on model parameters. Third, all parameters estimated in statistical models are associated with error (Section 5.3). Error in the estimation of a parameter is called standard error. An optional section (Section 5.4) explores how sample size is related to the power of a statistical model to make inferences about the world. Finally, this chapter ends with an applied case study of how well rich countries are meeting their obligations under the Monterrey Consensus on aid for poor countries (Section 5.5). This case study illustrates how standard errors can be used to make inferences in statistical models. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should be able to make informed inferences about parameters like means and regression slopes and to use these inferences to more accurately describe the social world.

5.1. From descriptive statistics to inferential statistics Like most people around the world, Americans are getting fatter. This is a serious problem, because obesity is closely linked to a range of health problems including diabetes, joint problems, and heart disease. Many people also consider obesity unattractive, and want to weigh less than they do. According to data from the US Health and Nutrition Examination Survey (NHANES), the mean weight of Americans aged 20-29 is 155.9 lbs. for women and 188.3 lbs. for men. These figures are up dramatically from the first time the NHANES was conducted. Then, in the early 1960s, the means for American women and men in the 20s were 127.7 lbs. for women and 163.9 lbs for men. Means and standard deviations for the weights of American twentysomethings, broken down by gender, are reported in Figure 5-3.

Clearly, the 672 women surveyed in the 1960-1964 NHANES recorded much lower weights than the 706 women surveyed in the 2003-2006 NHANES. Does that mean that women really were lighter in the 1960s? It probably does, but both means are associated with large amounts of error. There is error in the mean model because every person in the NHANES database deviates from the national mean for various different reasons. Potential reasons why an individual person's weight might deviate from the mean weight for people of the same gender nationwide might include things like: A person's height How much a person eats How much a person exercises A person's genetic tendency to store energy as fat The 672 women represented in the first column of Figure 5-3 had a mean weight of 127.7 lbs. Of course, they did didn't all weigh 127.7 lbs. Even in the early 1960s, not everyone looked like Marilyn Monroe. Given the standard deviation of 23.3 lbs. reported in Figure 5-4, most women in their 20s would have weighed between 104.4 and 151.0 pounds. A made-up sample of some of the 672 women from the 1960-1962 NHANES and the reasons why they might have deviated from the national mean weight is presented in Figure 5-4. In reality, each woman would have had hundreds or thousands of individual reasons for deviating from the mean. Everything we eat or drink, every step we take, and even the amount of time we spend sleeping can affect our weight. Even a woman who weighs exactly the mean weight might have reasons for being heavier than the mean and reasons for weighing less than the mean that just happen to cancel each other out.

The mean and standard deviation of women's weights are compared to the mean and standard deviation of the error in the mean model for weight in Figure 5-5. The only difference between the two sides of Figure 5-5 is the scale. On the left side, the women's weights are spread around the mean (127.7 lbs.). On the right side, the women's weights are spread around 0. The amount of spread in both cases is the same (standard deviation = 23.3 lbs.).

The mean model used to describe women's weights summarizes the characteristics of the data we actually have on weights in a simple descriptive model. Descriptive statistics is the use of statistics to describe the data we actually have in hand. A mean model of women's weights tells us the observed mean weight of the specific women in our databases. Similarly, regression models tell us the observed slopes and intercepts of regression lines for the data in our databases. These means, slopes, and intercepts are the parameters of models as observed using actual data. Observed parameters are the actually observed values of parameters like means, intercepts, and slopes based on the data we actually have in hand. Descriptive statistics is focused on finding and reporting observed parameters. It may seem like finding and reporting observed parameters is what statistics is all about, but the fact is that observed parameters are only the beginning of the story. We're not really interested in the actually observed weights of the 672 twentysomething American women who were included in the 1960-1962 NHANES database. What we're really interested in is making inferences about the true mean weight of American women in general of about the true difference between women's weights in 1960-1962 and women's weights in 2003-2006. Inferential statistics is the use of statistics to make conclusions about characteristics of the real world underlying our data. We've already used mean and regression models to make inferences about the real world, but we've done so informally. With the move from descriptive statistics to inferential statistics, we'll start using statistics to make formal inferences about characteristics of the real world behind our data. Observed parameters are descriptive statistics. They say something about the data themselves, but nothing about the larger world. They say that the weights of these 672 particular women averaged out to 127.7 lbs. on the particular days they were weighed using the particular scales in their particular doctors' offices. We can use this information to make inferences about the larger world, but it's like circumstantial evidence in a criminal case. After all, the NHANES was conducted over a three-year period, but every hour of every day you gain or lose weight. Your weight changes every time you eat or drink, or even breath. You're sweating, losing hairs, and shedding skin all the time. Your body structure is always changing as you gain or lose fat, muscle, or bone. In short, your weight is constantly changing. As a result, your observed weight at any one point in time is not the same thing as your "true" weight. True parameters are the true values of parameters like means, intercepts, and slopes based on the real (but unobserved) characteristics of the world. Your observed weight may be changing all the time, but still it tends to maintain roughly the same weight from month to month and year to year. At any one point in time there's a weight around which your body varies. This is your true weight. If you weighed yourself every hour on the hour for a whole year and took the mean of all these observed weights, the mean would be something like your true weight. The goal of inferential statistics is to make inferences about the true values of parameters. The observed values of parameters are a good guide to the likely true values of parameters, but observed parameters are always include some error. Inferential statistics is focused on understanding the amount of error in observed parameters. This amount is then used to make inferences about how much true parameters might differ from observed parameters. For example, the observed mean weight of American twentysomething women in 1960-1962 was 127.7 lbs. Is it possible that the true mean weight of American twentysomething women in 196-1962 was 128 lbs.? Maybe. Is it possible that their true mean was 130 lbs.? Unlikely. Is it possible that their true mean was 155.9 lbs., the same as women in 2003-2006? Impossible. Inferential statistics will allow us to make conclusions like this with confidence.

5.2. Types of error The island of Taiwan has had a difficult history. Long a part of China, it was subjected to 50 years of Japanese occupation from 1895-1945. Then in 1949 1.5 million mainland Chinese refugees from the Communist takeover of China flooded into Taiwan, swelling the population from 6 million to 7.5 million in one year. From 1950 through 1991 Taiwan was ruled by a military government that was dominated mainly by Chinese who had fled to the island in 1949. In short, for nearly a century before 1991 Taiwan was ruled by one form of dictatorship or another. No one alive in Taiwan today ever experienced democracy before the first free elections in 1991. As a result, younger Taiwanese have grown up under democracy, but older Taiwanese have strong memories of living under dictatorship. Are Taiwanese people today happy with the state of their democracy? Everywhere in the world social scientists find that people desire more democracy than they feel they have. The difference between people's desire for democracy and people's perception of how much democracy they actually have is called the "democratic deficit." Like people around the world, people in Taiwan feel that they do not have a democracy. People's ratings of democracy in Taiwan can be studied using data from the World Values Survey (WVS), which was conducted in Taiwan in 2006. The democracy rating has been scored on a scale from 0 to 100 where: Rating = 0 means the respondent thinks there is not enough democracy in Taiwan Rating = 50 means the respondent thinks there is just the right amount of democracy in Taiwan Rating = 100 means the respondent thinks there is too much democracy in Taiwan The results of a mean model for the democracy rating in Taiwan are summarized in Figure 5-6. The mean rating of 38.8 indicates that most people in Taiwan think there is less democracy than they would like, just as in the rest of the world. Since the democracy rating score is less than 50, there is a democratic deficit in Taiwan. Of course, not everyone in Taiwan feels this way. The standard deviation of 14.1 indicates that there is a wide spread in attitudes toward democracy. Still, the deficit makes it is pretty clear that Taiwanese people as a whole would like more democracy than they feel they have. The mean score (38.8 points) is almost one full standard deviation below 50.

In the mean model, each person in Taiwan is modeled as having a score of 38.8, plus or minus some deviation or error. This error is known as model error. It doesn't necessarily mean that there was a mistake in measuring someone's democracy rating. It means that the model gave an expected rating -- 38.8 -- that for many people was in error. Most people don't have a democracy rating of exactly 38.8. They have scores that are either lower or higher. These lower and higher scores average out to an observed mean of 38.8 points. The goal of the mean model summarized in Figure 5-6 is to find the true mean of how people in Taiwan feel about democracy. We don't know the true mean, but we do know that the observed mean is 38.8 on a scale from 0 to 100. The observed mean might differ from the true mean due to error. Broadly speaking, there are three different types of model error in a mean model: Measurement error Sampling error Case-specific error Measurement error is error resulting from accidents, mistakes, or misunderstandings in the measurement of a variable. For example, a respondent might mark the wrong oval on a survey form, or a question might be badly worded. Respondents might not remember the answer to a question, or might misunderstand the question. In a telephone survey, the researcher might not hear the respondent correctly, or might type in the wrong answer. Accidents happen. Since the observed mean democracy rating is calculated from people's actual answers as recorded on the survey, it might differ from the true mean if these recorded answers are wrong. Sampling error is error resulting from the random chance of which research subjects are included in a sample. Taiwan today is home to 22.8 million people. Only 1216 of them were included in the survey. It is possible that these 1216 people are not truly representative of the Taiwanese population. Every person's rating of democracy in Taiwan is the result of millions of influences and experiences. Ideally, all of these typically Taiwanese experiences should be reflected in the people chosen for the survey. If the sum total of all these influences experienced by the people answering the survey differ from the sum total of the influences experienced by the population as a whole, the observed mean from the survey will differ from the true mean of the population as a whole. For example, the survey design might not include sampling for hospitalized or homeless people, and so their experiences would not be reflected in the observed mean. Case-specific error is error resulting from any of the millions of influences and experiences that may cause a specific case to have a value that is different from its expected value. Most of the error in any statistical model is case-specific error. Each person's unique experience of the world determines that person's views on subjects like democracy. Since everyone has a different experience of the world, everyone differs from the mean for different reasons and in different ways. People with different identities, backgrounds, or even moods the day the question is asked will give different answers. Since these characteristics of people are always changing, the observed mean at any one time may differ from the true mean of the research subjects in the study. Case-specific error is so large because every person's answer to any question represents a kind of a random sample of all the potential influences that can possibly be experienced in a society. In the mean model, the results of all of these different and unique experiences are lumped together into a the model error. Linear regression models, on the other hand, take some of those unique experiences and bring them into the model. The independent variable in a regression model represents some part of what makes each case unique. For example, one thing that shapes people's views on democracy is their age. Older Taiwanese people grew up under a military dictatorship. We might theorize that people who grew up under a military dictatorship would be thankful for any kind of democracy. One hypothesis based on this theory would be that older people would rate Taiwan's democracy more highly than younger people. The results of a linear regression model using age as the independent variable and democracy rating as the dependent variable are reported in Figure 5-7.

The slope reported in Figure 5-7 is positive. Each additional year of age is associated with a rise of 0.105 in the expected value of a person's democracy rating. Using the coefficients in Figure 5-7, we could calculate the expected value of a 20 year old Taiwanese person's rating of Taiwan's democracy as 34.223 + 20 x 0.105 = 36.323 on a scale from 0 to 100. The expected democracy rating for a 60 year old Taiwanese would be 34.223 + 60 x 0.105 = 40.523, or about 4 points higher. That's not a lot, but it does tend to confirm the theory that age affects people's ratings of democracy in Taiwan. At least part of the case-specific error in Taiwanese democracy ratings can be traced back to age. In fact, one way to think about what regression models do is to think of them as explaining part of the case-specific error in a mean model. This is very clearly illustrated in Figure 4-10 and Figure 4-16 in Chapter 4. In Figure 4-10, a large part of the case-specific error in smoking rates in the mean model for Canadian provinces (left side of the figure) was attributed to the average temperature in each province (right side). The standard deviation of the error in the mean model was 5.3%. After taking temperature into account, the standard deviation of the error in the regression model was just 3.8%. A big chunk of the case-specific error in the mean model disappeared in the regression model. This error that disappeared was the error due to the differences in temperature across Canadian provinces. In the example of democracy ratings in Taiwan, the mean model has an error standard deviation of 14.1 (on a scale from 0 to 100). The regression model error standard deviation (not reported in the regression table) is 14.0 (on a scale from 0 to 100). A very small portion (0.1) of the case-specific error in Taiwanese democracy ratings is due to age. It is small because the effect of age reported in the regression model (Figure 5-7) is very small. Age isn't a big determinant of democracy ratings in Taiwan, but it is a factor. It's a small part of what makes people differ from the overall mean for Taiwan. Measurement error, sampling error, and case-specific error can be present in any statistical model, but most of inferential statistics focuses on case-specific error. Regression models in particular focus on attributing part of the case-specific error in dependent variables to the research subjects' scores on the independent variables. Measurement error and sampling error do affect regression models, but in very subtle ways. These are discussed in Chapter 12. Until then, when discussing model error we will focus exclusively on case-specific error.

5.3. The standard error of a parameter The large amount of error in statistical models can make it difficult to make inferences. Returning to the example of the race gap in wages (Figure 5-1), can we have any confidence that the true means of black and white wages are at all close to the observed means of $22,723 and $30,096? On the one hand, there is a very large amount of error in these mean models. On the other hand, the means in both models are based on very large samples of cases (633 blacks and 4331 whites). When a model is estimated using a large number of cases, the case-specific errors tend to cancel each other out. There may be an enormous amount of case-specific error (as in Figure 5-1), but if all the positive errors are balanced by negative errors, the observed mean might be very close to the true mean. Error is only a problem if, just by chance, there is too much positive error or two much negative error. The power of large numbers of cases to even out errors and produce a more accurate observed mean can be illustrated using the sample data on the weights of American women presented in Figure 5-4. Imagine if we tried to calculate the mean weight of American women in the 1960s using the weight of just one random woman. We might pick woman 3 and get a mean weight of 140.0 lbs. or woman 6 and get a mean weight of 115.6 lbs. If we based our mean model on just one woman's weight, there would be a lot of error in our observed mean. In fact, using just one case to calculate a mean in a mean model would give a range of means that had exactly the spread as the women's weights themselves. The mean calculated based on one case could be anything from 99.5 lbs. (the weight of woman 4 in Figure 5-4) to 177.7 lbs. (the weight of woman 9). A mean model estimated using just two cases would give a much more accurate observed means. The two lightest women in Figure 5-4 weigh 99.5 lbs. (woman 4) and 109.1 lbs. (woman 5). The mean of these two cases is 104.3 lbs. The mean of the two heaviest women (women 3 and 9) is 158.85 lbs. Thus a mean model based on any two random cases from Figure 5-4 would come up with an observed mean somewhere between 104.3 and 158.85 lbs. This compares to a range for one case of between 99.5 lbs. and 177.7 lbs. The range of possible means is narrower for two cases than for one case. For three cases, it would be even narrower. Once you get up to 672 cases, case-specific error is almost guaranteed to average out across all the cases. It turns out that the accuracy of parameters like means, slopes, and intercepts increases rapidly as more and more cases are used in their estimation. As sample sizes get larger, the observed levels of parameters get closer and closer to their true levels. There is always the potential for error in the observed parameters, because there is always case-specific error in the variables used in the models. Nonetheless, when models use large numbers of cases, the amount of error in observed parameters can be very small. Standard error is a measure of the amount of error associated with an observed parameter. The standard error of an observed parameter tells us how close it is likely to be to the true parameter. This is extremely important, because it enables us to make inferences about the levels of true parameters like means, slopes, and intercepts. Standard error depends on the number of cases used and on the overall amount of error in the model. Standard error is easy to calculate in mean models, but follows a more complicated formula in regression models. The calculation of standard error is covered in Section 5.4. As with the standard deviations of variables, statistical software programs routinely calculate the standard errors of all parameters. For the purpose of understanding where standard errors come from, it's enough to know that as the numbers of cases go up, the standard errors of parameters go down. Smaller standard errors mean that observed parameters more accurately reflects true parameters. Returning to the race gap in income (Figure 5-1), the observed mean income for twentysomething blacks was $30,826. This mean model had a very high error standard deviation ($22,723). It turns out that the standard error of the observed mean in this model is just $903. The standard error of a parameter can be interpreted in roughly the same way as the standard deviation of a variable: most of the time, the true mean is somewhere within one or two standard errors of the observed mean. So in Figure 5-1 the observed mean income for blacks is $30,826 with a standard error of $903. This implies that the true mean income for blacks is probably somewhere in the neighborhood of $29,900 to $31,700. The standard error of the mean income of whites is even smaller. Because of the large number of cases for whites (4331) the standard error of the mean is just $457. The regression of income on race in Figure 5-2 reported a slope of -6656, meaning that the observed race gap in income was $6656. The regression model had a very high level of error (regression error standard deviation = $29,263). Nonetheless, the standard error of the slope is just $1245. This means that the true race gap in income is likely somewhere between $5400 and $7900. The true race gap might be equal to exactly $6656 (the observed gap), but it probably isn't. Nonetheless, it's probably close. Based on the standard error of $1245, we can infer that it almost certainly isn't $0. In other words, we can infer that the race gap in incomes really exists. It's not just a result of random error in our data.

5.4. Sample size and statistical power (optional/advanced) The calculation of the standard error of a mean in a mean model is relatively straightforward. It is equal to the standard deviation of the variable divided by the square root of the number of cases. The calculation of the standard error of a regression slope is much more complicated. Like the standard error of a mean, it depends on the regression error standard deviation and the number of cases, but it also depends on the amount of spread in the independent variable. From a conceptual standpoint, the standard error of the slope is like stretching out the standard error of the mean of the dependent variable over the range of the independent variable, much like the values of the independent variable are spread over the range of the independent variable in Figure 4-10. The calculation of the standard error of a regression intercept is even more complicated. With all parameters, though, the standard error declines with the square root of the number of cases. This means that you can make more accurate inferences when you have more cases to work with. Because of the square root relationship, the number of cases is usually more important than the amount of model error for achieving a low standard error. Even models with enormous amounts of error (like the regression of Taiwanese democracy ratings on age) can have very low standard errors for their parameters, with enough cases. The relationship between the number of cases used in a mean model (N) and the standard error of the observed mean (SE) is depicted graphically Figure 5-8. The line on the graph can be read as the standard error of the mean of a variable when the standard deviation of the variable is equal to 1. The standard error of a mean goes down very rapidly as the number of cases rises from 1 to 20. Between 20 and 100 cases the standard error of a mean also declines rapidly, but not so steeply as before. After about 100 cases the standard error of a mean continues to fall, but at a very slow pace. Broadly speaking, once you have 1000 or so cases in-hand, enormous numbers of additional cases are needed to make any real difference to the standard errors of the mean. Sample sizes of N = 800 - 1,000 cases are sufficient for most social science applications.

In the regression model for Taiwanese democracy ratings (Figure 5-7) the observed slope was just 0.105, meaning that every extra year of age was associated with a 0.105 point increase in a person's democracy rating. We found that only a tiny portion (0.1 point out of 14.1 points) of the total case-specific error in people's democracy ratings could be attributed to age. Nonetheless, due to the large number of cases used in the model (1216 people), the standard error of the observed regression slope is just 0.25 points. Based on this figure, we can infer that the true effect of a year of age on people's democracy ratings likely lies somewhere between (roughly) 0.080 and 0.130. In other words, we can infer that the true effect is age is almost certainly not 0. Despite the enormous amount of error in the regression model, we can still make conclusions about how attitudes change with age with confidence. This ability to make conclusions about a true mean using an estimate of the mean based on real data is called the power of a statistical model. The power of any statistical model rises as the number of cases rises both because more cases means lower standard errors and (much less importantly) because more cases means more degrees of freedom in the model, and thus smaller error standard deviations. Both of these contributions to the power of a statistical model show diminishing returns once the sample size reaches 1,000 or so cases. Since most quantitative research in the social sciences is based on survey data and most surveys cost a fixes amount of time and money for each additional respondent, most studies are based on 800 or so cases. After surveys have about 800 respondents, they add very little additional power for each additional person.

5.5. Case study: Aid generosity and the Monterrey Consensus At the 2002 United Nations International Conference on Financing for Development in Monterrey, Mexico the rich countries of the world made a commitment to raise their levels of foreign aid to 0.70% of their national income levels. Many of the richest countries in the world have done this. Figure 5-17 shows levels of rich countries' overseas development assistance (ODA) spending as a proportion of national income for 20 rich countries. Each country's level of foreign aid is represented by a bar. Descriptive statistics can be used to describe the observed distribution of ODA spending. The observed mean level of aid across all 20 countries is 0.52% of national income. This and the Monterrey target of 0.70% of national income are marked on the chart. The observed mean is 0.18% less than the target. Though the observed mean is well below the target level, is it possible that the true mean of ODA spending as a percent of national income might really be equal to 0.7%?

The observed mean may differ from the true mean for a variety of reasons. Although the observed mean level of aid spending across all 20 countries is less than the target level of 0.70%, 5 countries have aid levels above the target and one more comes reasonably close to the target. If all 20 countries were targeting aid levels of 0.70%, it seems possible that 5 would overshoot, 1 could come close, and 13 would undershoot the target. There may be measurement error in countries' reported levels of ODA spending due to poor accounting practices or researcher mistakes. More likely, there is probably a lot of case-specific error. Countries may have targeted 0.7% but underspent due to the recession or overspent due to emergency spending on a humanitarian crisis. There's no sampling error in this example because the data represent all the world's richest countries, not a sample of rich countries. The standard deviation of ODA spending is 0.27%. There are 20 countries in the analysis. These two figures can be used to calculate the standard error of the mean of ODA spending, which comes out to 0.06%. Based on this standard error, inferential statistics can be used to make inferences about the true mean level of ODA spending. A standard error of 0.06% means that the true mean level of ODA spending is probably in the range of 0.46% to 0.58% (plus or minus one standard error from the observed mean). It is possible that the true mean is even farther from the observed mean, but it is very unlikely that the true mean is 0.70%. The Monterrey target of 0.70% is a full three standard errors away from the observed mean of 0.52%. The true mean level of ODA spending may not be 0.52%, but it is almost certainly not 0.70%. The rich countries of the world must increase ODA spending dramatically in order to meet their Monterrey obligations.

Chapter 5 Key Terms

Case-specific error is error resulting from any of the millions of influences and experiences that may cause a specific case to have a value that is different from its expected value.
Descriptive statistics is the use of statistics to describe the data we actually have in hand.
Inferential statistics is the use of statistics to make conclusions about characteristics of the real world underlying our data.
Measurement error is error resulting from accidents, mistakes, or misunderstandings in the measurement of a variable.
Observed parameters are the actually observed values of parameters like means, intercepts, and slopes based on the data we actually have in hand.
Sampling error is error resulting from the random chance of which research subjects are included in a sample.
Standard error is a measure of the amount of error associated with an observed parameter.
True parameters are the true values of parameters like means, intercepts, and slopes based on the real (but unobserved) characteristics of the world.

Statistical Inference Using the t Statistic

One of the biggest changes in society over the past fifty years has been the expansion of economic rights for women. More women have jobs outside the home than ever before, and women are able to work in a wider variety of jobs than ever before. Women still face many challenges including discrimination in the workplace, but high-paying jobs are no longer reserved just for men. Opportunities are becoming more equal. It is not so long ago that many careers were closed to women. The women who made up the original survey sample for the US National Longitudinal Survey of Youth (NLSY) were born in the years 1957-1964. These women started their careers in the early 1980s, at a time when most professions were open to women but serious wage discrimination still existed. In many cases these women were also expected to put childcare responsibilities ahead of career development. Today, as these women near retirement, the discrimination they faced over the decades probably means that they are still making less money than the should be given their knowledge and experience. They suffered a lifetime of challenges that helped open opportunities for the women of the future. The daughters of these women were mainly born in the 1980s They entered the labor market in the 2000s. These women are experiencing much less wage discrimination than their mothers did. As a result, we might hypothesize that the daughters of the original NLSY women would earn higher wages than their mothers did before them. A database comparing NLSY daughters' wages to their mothers' wages is illustrated in Figure 6-1. Daughters' wages are taken from the 2008 NLSY and pertain to wages earned in the calendar year 2007. Only daughters who were approximately 23-30 years old at this time are included. Mothers' wages are taken from the 1988 NLSY and pertain to calendar year 1987, when they were also 23-30 years old. The mothers' wages have been adjusted for inflation. Only daughters and mothers who reported having wage income are included in the database (those with no income or missing income are excluded). The first 30 rows of the database are shown in Figure 6-1, but the full database contains a total of 642 daughter-mother pairs. The database includes 7 columns. The first two are metadata items: the daughters' and mothers' case identification numbers. The five variables included in the database are: B.YEAR -- the year of the daughter's birth D.WAGE -- the daughter's wage income in 2007 M.WAGE -- the mother's wage income in 1987 M.ADJ -- the mother's wage income adjusted for inflation to 2007 dollars DIFF -- the difference between each daughter's wage income and her mother's wage income, or how much more the daughter makes than the mother did

Descriptive statistics for the daughters' wages and their mothers' wages (adjusted for inflation) are reported in Figure 6-2. The observed mean of the daughters' wages ($23,881) is much higher than the observed mean of their mothers' wages ($17,181). This suggests that there has been real generational change in women's employment opportunities.

Inferential statistics can be used to make conclusions about the intergenerational daughter-mother difference in wages with a high degree of confidence. The observed mean of the daughter-mother difference in wages is $6700. The standard error of this mean difference in wages is just $792. This implies that the true mean difference in wages is somewhere in the vicinity of $5900 to $7500. It may fall somewhere outside this range, but it is extremely unlikely give the observed mean and standard error that the true mean of the difference in wages could be $0. We can confidently conclude that the employed NLSY daughters make more money than their mothers did twenty years earlier. At first glance, this is a surprising result. The standard deviation of the difference in wages is very large. The observed mean difference in wages is $6700, but the standard deviation is nearly three times as big: $20,071. There are many reasons for the massive amount of error in the difference in wages. First, incomes are notoriously difficult to measure. People often don't know their incomes in detail, and even more often lie about their incomes. Second, there may be sampling error in the data, since only 642 daughter-mother pairs are being used to represent the entire female population of the United States. Third and most important, people's incomes vary widely. Differences in education levels, career choice, ability, personality, and personal connections all create case-specific error in incomes. The reason we can be so confident about the size of the mean of the difference in wages despite all this error is that the mean difference is calculated based on a large number of cases (N = 642). The use of a large sample drives down the standard error of the mean. In effect, all those sources of error tend to cancel each other out. The result is that the observed mean is probably pretty close to the true mean. How close? The standard error is a useful guide to the likely value of the true mean, but what we really need is a way to determine the actual probabilities of different values of the true mean. In regression models, we'd like to know the actual probabilities of different values of the slope. In order to judge the importance or significance of the results of a statistical model, we need more detailed information about the distributions of true means and slopes.

This chapter shows how formal inferences can be made about the likely ranges of the true values of the parameters of statistical models. First, observed parameters and their standard errors can be combined to calculate a new measure called the "t" statistic (Section 6.1). The t statistic is a measure of how big an observed parameter is relative to its standard error. Second, t statistics can be used to determine whether or not a true mean is significantly different from zero (Section 6.2). This is especially important in the study of paired samples, like daughters and their mothers. Third, t statistics can also be applied to regression slopes(Section 6.3). The t statistic of a regression slope can be used to infer whether or not a regression model adds any explanatory power compared to a simple mean model. An optional section (Section 6.4) demonstrates how the t statistic can be used to make inferences about how true means differ from specific target levels. Finally, this chapter ends with an applied case study of the relationship between poverty and crime for a large selection of US counties (Section 6.5). This case study illustrates how t statistics can be used to make inferences about means and regression slopes. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should be able to make formal inferences about the statistical and substantive significance of the parameters of statistical models.

6.1. The t statistic Standard errors are a lot like standard deviations. Every variable has a mean and a standard deviation. Standard deviations are meaningful because in the majority of cases the value of a variable falls within one standard deviation either direction of its mean. In nearly all cases the value of a variable falls within two standard deviations either direction of its mean. Any case that falls more than two standard deviations away from the mean is exceptional and likely to be an outlier. On the other hand, parameters like means, slopes, and intercepts have standard errors. Most of the time the true parameter of a model falls within one standard error of the observed parameter. The true parameter is almost always within two standard errors of the observed parameter. Standard errors, however, also have one more very important property. It is possible to prove mathematically that true parameters differ from observed parameters with an exact probability that can be calculated from the standard error of the parameter. The main difference between a standard deviation and a standard error is that a standard deviation describes a collection of data points (like a variable) while a standard error describes an observed parameter (like a mean, slope, or intercept). Standard errors represent the amount of error in the observed parameters. Standard deviations are used to calculate standard errors, but standard errors are much smaller than standard deviations. The key differences between standard deviations and standard errors and how they are used are summarized in Figure 6-3.

In inferential statistics standard errors are used to make inferences about the true values of parameters. For example, we often want to know the value of a true mean. We know the values of observed means of variables, and we know that the true means of variables are probably close to their observed means, but never know for certain exactly what the true means are. The standard error of the observed mean of a variable helps us make inferences about the probably value of its true mean. In Figure 6-2, it's very important (from a social policy perspective) to know whether or not the true mean of the daughter-mother difference in wages in wages might be zero. If the true mean were zero, that would mean that women were making no progress at all in fighting discrimination in the workplace. The observed mean difference in wages is $6700 with a standard error of $792. Another way of saying this is that the observed mean is 8.46 standard errors away from 0. If you started at $6700 and subtracted one standard error, you'd get $5908. If you went down a second standard error, you'd get to $5116. If you went down a third standard error, you'd get to $4324. You'd have to go down 8.46 standard errors to get to $0. If the true mean difference in wages really were $0, the observed mean would be off by 8.46 standard errors. Statisticians call this ratio of an observed parameter to its standard error the "t" statistic. t statistics are measures based on observed parameters that are used to make specific inferences about the probabilities of true parameters. The label "t" doesn't actually stand for anything. By an accident of history, the person who first calculated the t statistic in 1908 had used "s" to represent the standard deviation and "t" just happened to be the next letter of the alphabet. The t statistic is a measure of how big a parameter is relative to its standard error. The t statistic of a parameter can be calculated very easily by dividing a parameter by its standard error, but it's usually unnecessary to do the calculation yourself. Statistical software programs routinely report t statistics alongside parameters and their standard errors. The t statistic measures the size of a parameter. When an observed parameter has a large t statistic, we can infer that the true parameter is significantly different from 0. For example, a t statistic of 10 means that a parameter is 10 times as large as its standard error and is thus 10 standard errors away from 0. This is a large and significant difference. Statistical significance is when a statistical result is so large that is unlikely to have occurred just by chance. An observed parameter that has a t statistic larger than 2 is usually statistically significantly different from 0. In the NLSY women's wages example (Figure 6-2), the t statistic for the observed mean of the daughter-mother difference in wages is 8.46. This is much bigger than 2. We can infer that the true mean daughter-mother difference in wages is very significantly different from $0. Statistical computer programs can tell us exactly how statistically significant this result is. Statistical software can be used to calculate the exact probability of finding a t statistic of any given size. This probability is based on the numbers of degrees of freedom in a model. For example, the mean model for the daughter-mother wage gap in Figure 6-2 is based on 642 cases. Since the mean model uses 1 parameter, the model has 642 - 1 = 641 degrees of freedom. A computer program can tell us that when the t statistic of an observed mean is 8.46 with 641 degrees of freedom, the probability that the true mean could be something like $0 is 0.000000000000018%. In other words, the true mean is certainly not $0. Technically, what the probability of the t statistic tells us is that "the probability that the true mean could be 8.46 or more standard errors in either direction away from the observed mean of $6700 is 0.000000000000018%." So technically, this probability is the probability that the true mean could be $0, less than $0, $13400, or greater than $13400. The practice in some disciplines (like psychology) is to break out these probabilities into different "tests" and perform "1-tailed" and "2-tailed" analyses. In the social sciences, the usual practice is much more straightforward. The probability of the t statistic is simply considered to be the probability that the parameter is significantly different from 0. Figure 6-4 gives some idea of how big a t statistic has to be to be considered statistically significant. Figure 6-4 reports the probability associated with a t statistic with 641 degrees of freedom (as in the daughter-mother wage example). The actually observed t statistic of 8.46 is off the chart. Social scientists usually consider a t statistic to be statistically significant if it is associated with a probability of 5% or less. So when an observed mean is so large (relative to its standard error) that the probability that the true mean could be 0 is under 5%, we proclaim the true mean to be statistically significantly different from 0.

For a mean model with 641 degrees of freedom, any t statistic greater than about 1.96 indicates that the true mean is significantly different from 0. As with other statistics, there's usually no need to calculate any of this. Statistical software programs can provide all the necessary information. For example, statistical software output reporting the results of a regression of smoking rates on temperature in Canadian provinces (Figure 4-9) would usually look something the table in Figure 6-5. While it is helpful to be able to understand the standard errors and t statistics, all you really need from the table is the probability. In the example of the Canadian provincial smoking rates, both the intercept (37.041) and the slope (-.443) for the effect of temperature on smoking are statistically significant.

6.2. Inferences using the mean model In the mean model, the t statistic is used to make inferences about the level of the true mean, but we're usually not very interested in true means. Usually the observed means are good enough. For example, the observed means for daughters' and mothers' wages for the NLSY sample (Figure 6-2) are $23881 (daughters) and $17181 (mothers). The t statistic for daughters' wages is 36.1 and the t statistic for mothers' wages is 33.2 (both with 641 degrees of freedom). The very large t statistics tell us that the true means of both daughters' and mothers' wages are significantly different from $0. That's correct, but not very interesting. Of course their true wages are different from $0. Why would they work if their employers paid them $0? The t statistic is only really useful in mean models when there's some reason to demonstrate that the true mean couldn't be 0. This usually happens when pairs of linked cases are being compared, like when daughters' incomes are compared to their mothers' incomes. Paired samples are databases in which each case represents two linked observations. With paired samples, often what we want to know is whether or not the true mean of a variable has changed significantly from one time period to another. We know that the observed means have changed. If we survey 642 women in 1988, then survey their daughters twenty years later in 2008, it's almost impossible for the two means to be exactly the same. Just by chance one or the other will be higher. What we want to know is whether or not the mean twenty years later is significantly higher. With paired sample data, mean models are often used to make inferences about the true mean change over time. As with daughters' and mothers' incomes, there are often important social policy reasons for knowing whether or not change has occurred. For example, many people believe that schools today suffer because they spend too much time and money on social support services for children and families and not enough on education. There is a general impression in society today that schools now spend much more of their limited resources on student services instead of direct classroom instruction. Have schools really moved from a focus on education to a focus on social work? This is an ideal question for a mean model based on paired sample data. Figure 6-6 contains a database of school spending figures for the 50 US states plus the District of Columbia for 1988 and 2008. In addition to the usual metadata items there are six variables: EXPENDxxxx -- Total school expenditures in 1988 and 2008 SUPPORTxxxx -- Student support services expenditures in 1988 and 2008 Sup%xxxx -- Student support as a proportion of total expenditures in 1988 and 2008 Student support services expenditures include spending on school nursing, school psychology, counseling, and social work services. The 1988 figures have been adjusted for inflation to 2008 dollars. Note that all expenditures have risen in part because all state populations have increased since 1988 and in part because all states spend more on education per student than they did in 1988.

Descriptive and inferential statistics for the student support spending as a percentage of total educational spending are summarized in Figure 6-7. Descriptive statistics are reported for student support spending in 1988 and 2008 and for the change in student support spending. Inferential statistics are only reported for the change in student support spending over time. Inferential statistics about the level of student support spending in 1988 and 2008 would be meaningless, since the true means for both variables are clearly far greater than 0%.

The observed mean change in student support spending was 1.36%. Observed state spending on student support services has in fact gone up. Does this mean that states are truly focusing more on student support services than they did in the past? Or is this rise more likely just random variation from a true mean of 0% (indicating no change)? The probability of the t statistic can be used to make inferences about the true mean change over time. The t statistic for the change in student support spending is 2.21 with 50 degrees of freedom (there are 51 cases, so the degrees of freedom are 51 - 1 = 50). The probability associated with this t statistic is 0.039, or 3.9%. In other words, there is only a 3.9% chance that the true mean change in student support spending between 1988 and 2008 was 0%. Since the chance that there was no change in the true mean is less than 5%, we can infer that the true mean level of student support spending has changed between 1988 and 2008. States spent a significantly higher proportion of their budgets on student support services in 2008 than they did in 1988. The mean proportion of education spending that goes to student support services has clearly increased since 1988. The observed mean increase was 1.36% and the t statistic confirms that this increase was statistically significant. Does this mean that it is important? After all, the mean level of student support spending only increased from 34.04% to 35.40% over a twenty year period. In 23 states is actually went declined. These seem like very weak results on which to base social policy. The increase is statistically significant, but is does not seem large enough to be meaningful from a policy standpoint. Substantive significance is when a statistical result is large enough to be meaningful in the view of the researcher and society at large. The increase in student support spending since 1988 is statistically significant, but it's probably not large enough to be considered substantively significant.

6.3. Inferences about regression slopes In regression models, the t statistic is used to make inferences about the true slope. The t statistic can also be used to make inferences about regression intercepts, but this is rarely done in practice. While inferences about true means are only made in special situations (like with paired samples), inferences about true slopes are made all the time. It's so common to use t statistics with regression slopes that statistical software programs usually print out t statistics and their associated probabilities by default whenever you use them to estimate a regression model. In writing up statistical results in the social sciences, almost any regression slope is accompanied by a note reporting its statistical significance. Returning to the example of official development assistance (ODA) spending as a proportion of national income for 20 rich countries, a mean model for ODA spending is depicted on the left side of Figure 6-8. The observed mean level of ODA spending for the 20 rich countries is 0.52% (as noted on the chart), but individual countries deviate widely from this mean. Sweden (SWE) gives almost twice the mean level (1.01% of national income) while the United States (USA) gives much less than half the mean level (0.19% of national income). What makes some rich countries more generous than other countries in helping poor countries with ODA aid?

One theory to account for some of the case-specific error in the mean model might be that richer countries have more money to spend and so can afford to be more generous. There is wide variability among rich countries in just how rich they are. The poorest rich country is New Zealand (NZL) with national income of $27,940 per person, while the richest is Norway (NOR) with national income of $87,070 per person. The theory would suggest that Norway can afford to give much more in aid than New Zealand, and it does. Generalizing from these two cases, we might hypothesize that country ODA spending levels rise with national income levels. The right side of Figure 6-8 shows how ODA spending is related to national income levels. The hypothesis seems to be correct: a large part of the case-specific error in ODA spending can be attributed to differences in national income. From a descriptive standpoint, differences in national income account for a "large" amount of the case-specific error in ODA spending, but is the effect of national income statistically significant? Model 1 in Figure 6-9 reports the results of a regression of ODA spending on national income in thousands of dollars. The data for this and the other models reported in Figure 6-9 are taken from the database depicted in Figure 4-1. The slope for national income is 0.013, indicating that every $1000 increase in national income is associated with an expected increase of 0.13% in ODA spending. Based on the data we have, the probability that the true slope for national income might really be 0 is tiny. We can infer that the true slope for national income is almost certainly not 0. National income has a highly significant impact on ODA spending.

What other factors might explain some of the case-specific error in ODA spending levels? The results of two more regression models are reported in Figure 6-9. In Model 2, ODA spending is regressed on European status (as in Figure 4-3). The observed slope is 0.328. This represents the observed difference in mean ODA spending between non-European and European countries. European countries tend to give 0.328% more in ODA than non-European countries. The probability of the t statistic associated with this slope is 0.013 (or 1.3%), indicating that there is only a tiny chance that the true slope for European status is 0. Based on the small probability that the true slope is 0, we can infer that the true slope is not 0. We can infer that European countries are significantly more generous than non-European countries. Model 3 illustrates a non-significant slope. In Model 3, ODA spending is regressed on administrative efficiency (administrative costs as a percentage of total official development assistance). We might hypothesize that part of a country's case-specific deviation from the mean level of ODA spending could be due to high administrative costs. If administrative costs are high, ODA spending would be high, because the total level of spending equals a country's true "generosity" in giving aid plus its costs in administering its aid budget. The observed regression slope of -.003 indicates that this is not in fact what happens. High administrative costs are actually associated with less ODA spending, not more. The observed effect of administrative costs is very small, but it is definitely negative, not positive. The observed effect of administrative costs on ODA spending may negative, but the effect is not significantly different from 0. The probability of .927 for the t statistic for the slope of administrative costs indicates that there is a 92.7% chance that the true slope could be 0 (or as far away from the observed slope as 0 is). We would infer from this that administrative costs have no significant effect on ODA spending. Another way of thinking about a non-significant slope is depicted in Figure 6-10. Figure 6-10 contrasts the mean model for ODA spending (left side) with a regression model for ODA spending based on administrative costs (right side). Thought the regression line does slope slightly downward, the scatter plot on the right side of the chart doesn't particularly move with the line. This is very different from the right side of Figure 6-8, where the scatter plot tracks the line much more closely. Figure 6-10 illustrates a situation in which only a small part of the case-specific error in the mean model for ODA spending is explained by the regression model. When a regression model explains very little of the case-specific error in the dependent variable, the slope tends to be small and not statistically significant.

6.4. One-sample t statistics (optional/advanced) The t statistic associated with a parameter is usually used to make inferences about whether or not a true parameter is significantly different from 0. By default, this is how all statistical software programs are programmed to use the t statistic. Nonetheless, sometimes social scientists want to make other inferences about true parameters. It takes some extra work, but is it possible to use t statistics to evaluate whether or not true parameters are significantly different from any number, not just 0. This is most commonly done in mean models. In regression models, we almost always want to know whether or not the line truly slopes, and nothing else. In mean models, on the other hand, we often want to know whether or not the true mean hits some target or threshold. This can be illustrated once again using the data on ODA spending levels. The observed mean level of ODA spending across the 20 rich countries listed in Figure 4-1 is 0.52%. As discussed in Chapter 5, these countries agreed a target level for ODA spending of 0.70% of national income. The standard error of ODA spending was used in Chapter 5 to argue that it is "very unlikely" that the true mean level of ODA spending met the target of 0.70%. Just how unlikely is it? One way to answer this question would be to construct an artificial paired sample database. Each country's actual level of ODA spending could be paired with the target level of 0.70% and the difference calculated. This is done in Figure 6-11. The t statistic for the mean difference between actual and target ODA spending is 3.03 with 19 degrees of freedom. The probability associated with this t statistic is just 0.007 (0.7%). In other words, there is only a 0.7% chance that countries are truly meeting their target of spending 0.7% of national income on ODA (the fact that both figures are 0.7 is just a coincidence). The true mean spending level falls significantly short of the 0.7% target.

Another, more direct way to answer the question would be to compare the observed mean to 0.70%. The observed mean level of ODA spending is 0.518%. This is 0.182% short of the target level. The standard error of this observed mean is 0.060%. As discussed in Chapter 5, the observed mean is 3 standard errors lower than 0.70 (it's actually 3.03 standard errors, as shown in Figure 6-11). Since the observed mean is 3.03 standard errors away from the target, the t statistic for the difference between the observed mean and the target is 3.03. A t statistic of 3.03 with 19 degrees of freedom has a probability of 0.007. This is the same result as found using the paired sample design. The true mean level of ODA spending is significantly less than 0.7%. This use of the t statistic is called a "one-sample" t statistic. It works because the difference between a mean and its target (used in the one-sample scenario) is the same as the mean of the differences between cases and their targets (used in the paired sample scenario). The one-sample t statistic can be used to evaluate the gap between an observed mean and any arbitrary target level of the true mean. In principle, the same logic can also be used to evaluate the gap between observed regression slopes and intercepts and arbitrary targets, but this rarely occurs in practice. A common use of the one-sample t statistic is to make inferences about sampling error. For example, according to the 2000 US Census the observed mean size of a US household was 2.668 persons. This figure is based on an actual count of the entire population, so while it may have measurement error and case-specific error, it has no sampling error. The observed mean size of a US household in the 2000 Current Population Survey (CPS) was 2.572 persons. The CPS is a sample survey of the US population that uses the same measures as the Census itself. The measurement error of the CPS should be identical to the measurement error of the Census, and the case-specific error of the CPS should be equivalent to the case-specific error of the Census. That means that the only difference between the CPS observed household size and the Census observed household size should be sampling error in the CPS. The difference between the Census observed mean of 2.668 and the CPS observed mean of 2.572 is 0.096 persons. The standard error of the CPS mean is 0.0057, giving a t statistic of 16.79. The CPS mean is based on 64,944 households. A t statistic of 16.79 with 64,943 degrees of freedom has a tiny probability that is very close to 0. From this we can infer that the CPS mean is significantly different from the Census mean. In other words, the level of sampling error in the CPS is statistically significant. On the other hand, the mean difference of 0.096 persons indicates that it is probably not substantively significant.

6.5. Case study: Poverty and crime Poverty is strongly associated with crime. Poverty is usually measured as a lack of money income. People who live in households with less than a certain income threshold are considered to live in poverty. The exact income threshold depends on the country, household size and composition, and sometimes on the area within the country. In the United States, the overall national poverty rate has been stable at around 12.5% of the population for the past forty years. Since the whole concept of poverty is so closely tied to the idea of having too little money, one might expect poverty to be more closely related to property crime than to violent crime. If poverty is fundamentally a lack of money, then people in poverty might be expected to commit property crimes in order to gain more money. This is a materialist theory of poverty. On the other hand, it is possible that poverty is not fundamentally an economic phenomenon. It might be argued that poverty really means much more than just a lack of income. In this theory of poverty, living in poverty means living a life that is lacking in the basic human dignity that comes from having a good job, a decent education, and a safe home. If poverty has more to do with personal dignity than with income, poverty might be more closely related to violent crime than to property crime, as people lash out violently at loved ones and others around them in response to their own lack of self-respect. This is a psychosocial theory of poverty. Which is correct, the materialist theory of poverty or the psychosocial theory of poverty? In terms of specific hypotheses, is poverty more closely related to property crime or to violent crime? In the United States, poverty rates are available from the US Census Bureau for nearly every county, while crime data are available from the Federal Bureau of Investigation for most (but not all) counties (data are missing for many rural counties). All in all, both poverty and crime statistics are available for 2209 out of the 3140 US counties for 2008. In these 2209 US counties property crime rates are much higher than violent crime rates. Considering the two crime rates for US counties to be a paired sample, the observed mean violent crime rate of 85.9 crimes per 100,000 population is much lower than the observed mean property crime rate of 636.7 crimes per 100,000 population. The mean difference in the two crime rates is 550.8 with a standard error of 18.52. The t statistic associated with this mean difference is t =13.937 with 2208 degrees of freedom, giving a probability of .000 that the true levels of property and violent crimes are equal across the 2209 counties. Property crimes are indeed significantly more common than violent crimes. The difference is both statistically significant (probability = 0%) and substantively significant (the mean violent crime rate is 7.4 times the mean violent crime rate). The results of regressing both the property and violent crime rates on the poverty rates of the 2209 US counties are reported in Figure 6-12. Both slopes are positive and statistically highly significant. Every 1% rise in the poverty rate is associated with an expected increase of 13.0 per 100,000 in the property crime rate and an expected increase of 4.5 per 100,000 in the violent crime rate. Clearly, crime rates rise with poverty. The relative slopes seem to imply that poverty is more important for property crime than for violent crime, but the two slopes aren't really comparable. Since property crime is so much more common than violent crime, an extra point of poverty would be expected to cause more of a change in property crime rates than in violent crime rates.

The two t statistics, on the other hand, are comparable. The t statistics represent the statistical significance of each relationship. Put differently, the t statistics are related to how much of the county-specific deviation from the mean crime rate is captured by the regression models for property crime and for violent crime. The t statistic for violent crime is about 2.5 times as large as the t statistic for property crime. This implies that poverty explains much more of the variability in violent crime rates than the variability in property crime rates. In other words, poverty is more important for understanding violent crime than for understanding property crime. This tends to lend more support to the psychosocial theory of poverty than to the materialist theory of poverty. Poverty is not just a matter of money. It is also -- or maybe even more so -- a matter of dignity.

Chapter 6 Key Terms

Paired samples are databases in which each case represents two linked observations.
Statistical significance is when a statistical result is so large that is unlikely to have occurred just by chance.
Substantive significance is when a statistical result is large enough to be meaningful in the view of the researcher and society at large.
t statistics are measures based on observed parameters that are used to make specific inferences about the probabilities of true parameters.

Introduction to Multiple Linear Regression

Parents and politicians are forever convinced that their children are not getting a good enough education. In part to meet parents' and politicians' demands to compare educational outcomes across countries, the Organization for Economic Cooperation and Development (OECD) administers the Program for International Student Assessment (PISA). The program organizes standardized tests comparing the knowledge of 15 year old students across in OECD member and other countries. The PISA tests focus very heavily on the topics that parents and politicians seem to worry most about -- math and science -- while ignoring other subjects that are probably much more useful for ensuring a happy and successful life, like literature, the arts, and of course the social sciences. Nonetheless, countries' PISA test results can be used to help answer important social scientific questions about national educational outcomes. One concern that is often raised by parents and politicians is the small number of women who choose to enter scientific and engineering professions. This may or may not be a problem -- after all, saying that there's a shortage of women in the sciences is the same as saying that there's a shortage of men in other areas -- but it is widely perceived to be a problem. Many OECD countries (including the United States) have special government-funded programs to increase the numbers of girls who study science and the numbers of women who choose scientific careers. Parents and politicians are particularly concerned that teenage girls don't seem to do as well in science in high school as teenage boys. Do teenage girls really underperform teenage boys in science? Cross-national data from the PISA tests can be used to answer this question. Data on PISA science scores are reported in Figure 7-1.

In addition to the usual metadata items, Figure 7-1 contains seven variables: BOYS -- The national mean PISA science score for boys GIRLS -- The national mean PISA science score for boys GAP -- The gender gap in science education (BOYS - GIRL) INCOME -- National income per person in US Dollars SPEND -- Education spending as a percentage of total national income TEACHERS -- The number of teachers per 100 students The PISA scores are constructed to have a mean of 500 for the OECD as a whole. National scores above 500 are above the OECD mean, while national scores below 500 are below the OECD mean. Since each country has a science score for both girls and boys, the database in Figure 7-1 is a paired sample. The mean difference between boys' and girls' scores is 0.36 points (the boys' mean is 0.36 points higher than the girls' mean). This difference is associated with a t statistic of t = 0.31 with 44 degrees of freedom. Based on this t statistic, there is a probability of 0.759 that the true mean difference between boys and girls could be 0. Since this probability of 75.9% very high, we would infer that it is entirely possible that there is no true difference between boys' and girls' performance in science. Even though there is no evidence for a gender gap overall across the 45 countries, there are many individual countries that have large gender gaps. The thirteen countries with a gender gap greater than 5 points are listed in Figure 7-2. Policy makers in these countries might ask social scientists to explain the gender gap and then recommend policies that could help reduce it. Three theories that might explain the gender gap in science scores are: (1) Income -- Richer countries have greater gender equality and so girls in richer countries are encouraged to study science more than girls in poorer countries (2) Spending -- High levels of educational spending tend to even out performance for all students, while countries that spend very little on education may give preference to boys over girls (3) Teachers -- Girls tend more than boys to learn through personal interaction, so having more teachers and smaller class sizes benefits girls' education more than boys' education

Each of these theories can be operationalized into a specific hypothesis using the data reported in Figure 7-1. The income theory predicts that countries that have higher income levels will have smaller gender gaps (as incomes go up, the gap goes down). The spending theory predicts that countries that spend more on education will have smaller gender gaps (as spending goes up, the gap goes down). Finally, the teachers theory predicts that countries that have more teachers will have smaller gender gaps (as the number of teachers goes up, the gap goes down). The results of regression models associated with each of these hypotheses are reported in Figure 7-3.

The results completely contradict the income theory. The slope in Model 1 of Figure 7-3 indicates that richer countries actually have bigger gender gaps than poor countries (though the effect is not statistically significant). On the other hand, the results do tend to confirm the spending theory, but the effect of spending is not statistically significant. In Model 2, the probability of 0.693 indicates that there is a very large probability that the true effect of spending is 0. The only strong result in Figure 7-3 is the slope for teachers. According to the slope in model 3, every additional teacher per 100 students tends to reduce the gender gap by more than 1 point. This result is unlikely to have occurred by chance (probability less than 2.3%). The policy implication seems to be that more teachers are required if a country wants to reduce its gender gap in science education. Obviously, hiring more teachers costs money. Yet the relationship between spending and the gender gap is not significantly different from 0. Moreover, it's possible that only rich countries can afford to increase their spending on education. In short, it is difficult to change any one of these three determinants of the gender gap without changing the others at the same time. What we really need is an integrated model that take all three variables into account at the same time. For that, new statistical tools are required.

This chapter introduces the multiple linear regression model. First, there is no reason why a regression model can't have two, three, or even dozens of independent variables (Section 7.1). The potential number of independent variables is limited only by the degrees of freedom available, but if there are too many independent variables none of them will be statistically significant. Second, the slopes of multiple regression models represent the independent effects of all of the independent variables on the dependent variable (Section 7.2). Regression models are often used to study the effect of one independent variable while "controlling for" the effects of others. Third, like any statistical model, multiple regression models can be used to predict values of the dependent variable (Section 7.3). Prediction in multiple regression works exactly the same way as when there is only one independent variable, just with additional variables. An optional section (Section 7.4) explains how control variables can be used to reduce the amount of error in regression models and thus indirectly boost the significance of regression coefficients. Finally, this chapter ends with an applied case study of the determinants of child mortality rates in sub-Saharan African countries (Section 7.5). This case study illustrates how regression coefficients can either increase or decrease when additional variables are added to a regression model. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should be able to use multiple regression to make basic inferences about the effects of multiple independent variables on a single dependent variable.

7.1. The multiple regression model Social scientists often have many competing theories to explain the same phenomenon. The gender gap in education might be due to national income, spending, or teachers. Countries' foreign aid spending levels might depend on their national incomes, European status, or aid efficiency levels. People's incomes might depend on their ages, races, genders, and levels of education. Moreover, these theories are not mutually exclusive. People's incomes differ by both race and gender, not one or the other. Most outcomes in the social sciences are the result of multiple causes. Models designed to study them must have multiple causes as well. Multicausal models are statistical models that have one dependent variable but two or more independent variables. Though many different kinds of multicausal models are possible, the most commonly used multicausal model is a straightforward extension of the linear regression model. Multiple linear regression models are statistical models in which expected values of the dependent variable are thought to rise or fall in a straight lines according to values of two or more independent variables. Multiple regression models work the same way as simple linear regression models except that they have additional independent variables. They produce expected values that are the values that a dependent variable would be expected to have based solely on values of the independent variables. They do this by determining the combination regression coefficients (slopes and intercepts) that minimizes the regression error standard deviation. In effect, multiple regression models take the observed values of the dependent variable and spread them out according to the values of two or more independent variables at the same time. An example of a social science phenomenon that has multiple causes is foreign aid. A multiple linear regression model for Official Development Assistance (ODA) spending is presented in Figure 7-4. This model integrates the three ODA spending models that were presented in Figure 6-9: one based on income (Model 1), one based on European status (Model 2), and one based on administrative costs (Model 3). In the simple linear regression models, both national income and European country status were found to be significantly related to ODA spending levels (the effect of administrative costs was non-significant). The multiple linear regression model (Model 4) spreads the total variability in ODA levels in the 20 rich countries across all three explanations at the same time. The coefficients in Model 4 represent the unique combination of coefficients that result in the smallest possible regression error standard deviation for the model as a whole.

In Model 4, the slope for national income is slightly smaller than it was in Model 1 (0.010 versus 0.013). Although it is smaller, it is still statistically significant (probability = .007 or 0.7%). As countries get richer, they give more of their national incomes in ODA spending. The slope for European status has also declined in Model 4, but much more so (from 0.328 to 0.199). The new, smaller slope for European status is no longer statistically significant (probability = 0.128 or 12.8%). European countries still have observed ODA spending levels that are 0.199% higher than non-European countries, but this difference is not statistically significant. In other words, the results reported in Model 4 indicate that the ODA spending difference between European and non-European countries could be due to random chance error. In Model 4 as in Model 3 administrative costs have no measurable impact on ODA spending. The mean level of ODA spending across all 20 countries is 0.52% of national income with a standard deviation of 0.268%. The regression error standard deviation for Model 4 is 0.185%. The multiple regression model has substantially less error than the simple mean model. A portion of countries' overall deviations from the mean spending level of 0.52% can be traced to countries' European status (European or non-European), but much more can be traced to countries' national income levels (rich versus poor). The contrast between the coefficients of European status in Model 2 versus Model 4 indicates that part of the difference between European and non-European countries' levels of ODA spending is due to the fact that European countries tend to be richer than non-European countries. This is illustrated in Figure 7-5.

The mean level of ODA spending for European countries is much higher than the mean level for non-European countries, but so is the mean level of national income. Do European countries spend so much on foreign aid because they're European, or because they're rich? The multiple regression model suggests that the true answer is a combination of the two explanations. European countries do spend a lot on ODA just like other rich countries do, but they spend even more than would be expected just based on their national income levels. How much more? The best estimate is that European countries spend 0.199% more of their national income on ODA than do other countries of similar income levels. This figure comes from the coefficient for European status in Model 4. The difference of 0.199% is not statistically significantly different from 0%, but it is still the best estimate of the difference. In other words, out best guess is that being European makes a country spend 0.199% more on aid than it otherwise would based on its income level alone. Just as European countries may spend more on aid because they have higher incomes, it is possible that higher income countries spend more on aid in part because many of them are European. In Figure 7-4, the slope for national income is 0.013 in Model 1, but this drops to 0.010 in Model 4. The slope for national income is lower in the multiple regression model (Model 4) than in the simple linear regression model (Model 1) because in the multiple regression model the total variability in ODA spending levels is split between national income and European status. Ultimately, what multiple linear regression does is split the total variability in the dependent variable among all the independent variables. In essence, the multiple independent variables are all competing for the same available variability. This usually (but not always) shows up as smaller slopes in the multiple regression model. In Figure 7-3 three different independent variables were used to explain the gender gap in science scores in three separate linear regression models. The three independent variables were national income, educational spending, and teachers per 100 students. Figure 7-6 presents a multiple linear regression model of the gender gap in science that uses all three variables. The slopes in Figure 7-6 are actually stronger, not weaker, than those from the original three models. This can only happen when the multiple independent variables complement each other, capturing different aspects of the dependent variable. Some countries have large gender gaps because they have high incomes but also have small gender gaps because they have lots of teachers. In the simple linear regression models these two effects cancel each other out, but in the multiple linear regression model the two separate effects are revealed.

Multiple liner regression is by far the most commonly used statistical model in the social sciences. It summarizes an enormous amount of information about how variables are related in a very compact space. Multiple regression tables always report the model intercept and the slopes of each of the independent variables. Sometimes they report the standard errors of the coefficients, sometimes the t statistics, and sometimes the probabilities of the t statistics. When social scientists want to report a large number of results in a single table, they report only the coefficients and use footnotes to indicate the probabilities of their associated t statistics, as illustrated in Figure 7-7. Because multiple regression tables contain so much information, an entire paper can be written around a single table of results. In short, multiple linear regression analysis is the workhorse method of social statistics.

7.2. Prediction using multiple regression Multiple linear regression models can be used to calculate predicted values of dependent variables in exactly the same way as simple linear regression. Since multiple linear regression models include more predictors than simple regression models, they tend to produce more accurate predictions. Predictors are the independent variables in regression models. A multiple regression model using four predictors to predict the incomes of employed American twentysomethings is presented in Figure 7-8. All four predictors (age, race, gender, and education) have highly significant slopes. Based on the t statistics, race is the least important of the four independent variables, but even race is highly significant statistically. Note that the intercept of this model is not very meaningful on its own, but is nonetheless necessary for calculating predicted values.

The equation for wage income based on the regression coefficients reported in Figure 7-8 is spelled out in Figure 7-9. Predicted income starts out at -$68,933 for a black female age 0 who has no education. Of course, this is a meaningless extrapolation of the regression analysis: newborn babies don't have incomes or education. Nonetheless, it is the starting point for calculating predicted values. Starting at -$68,933, each additional year of age brings $1843 in income, being white adds $4901 to a person's predicted income, being male adds $7625 to a person's predicted income, and each additional year of education brings $3599 in income. Using the equation in Figure 7-9, the incomes of any white or black Americans in their twenties can be predicted. The predictions may not be correct, but they will be more correct than simply predicting people's incomes based on the mean income for American twentysomethings.

The calculations for predicted wage income levels for 10 American twentysomethings are illustrated in Figure 7-10. The values in the table illustrate how a single regression model (Figure 7-8) can produce a very wide variety of predictions. The predicted incomes range from $21,885 for a 21 year old white male high school dropout to $61,822 for a 29 year old white male with an MBA. Lower and higher incomes are also possible. For example, a 21 year old black female high school dropout would be expected to earn just $9,359 per year. This is below the US minimum wage for a full-time worker, but the SIPP data are based on all employed people, including part-time employees. As predicted by the regression model, a 21 year old high school dropout might have trouble finding a full-time job.

Of course, most people have incomes that are very different from their predicted values. How different? Figure 7-11 reports the model error standard deviation for six different ways of predicting people's incomes. In the mean model, each person's income is predicted using the observed mean income for all 4964 American twentysomethings in the sample. The four simple regression models each use a single independent variable to calculate predicted values for income, while the multiple regression model uses all four independent variables together. The error standard deviation is based on the deviation from their expected incomes in each model for all 4964 people. The multiple linear regression model has less model error than any of the other models, but not much less. Even knowing people's age, race, gender, and education, it is very difficult to predict their incomes with accuracy.

7.3. The meaning of statistical controls When the purpose of multiple regression is to predict a specific outcome (like people's wage income levels), the statistical significance of the regression coefficients isn't really very important. Whether or not a true slope in a regression model is significantly different from 0 doesn't change the fact that the observed slope is the best available estimate of the true slope. In other words, when using regression for prediction the observed slopes are good enough. On the other hand, when using regression to evaluate hypotheses, the statistical significance of the slopes is crucially important. For example, in Figure 7-4 the observed slope for Administrative costs is so small that there is a very high probability that the true slope might be something like 0 (probability = 0.912 in Model 4). We infer from this that Administrative costs probably aren't an important cause of countries' ODA spending levels. Similarly, in Figure 7-6 the t statistic associated with Educational spending has a probability of 0.243, suggesting that Educational spending is not an important predictor of the gender gap in science scores. That's not surprising, since Educational spending was also not significant in its simple linear regression model (Model 2 in Figure 7-3). In contrast, National income was not significant in its simple linear regression model (Model 1 in Figure 7-3), but it is significant in the multiple regression model for the gender gap (Model 4 in Figure 7-6). In Figure 7-3, the observed slope for National income was 0.09 and the probability that the true slope might be 0 was 0.208. In Figure 7-6, the observed slope for National income was 0.16 and the probability that the true slope might be 0 was 0.048. Is the true slope for National income 0 or isn't it? Do richer countries have wider gender gaps or not? The simple answer to this question comes from the simple linear regression: higher National income is associated with higher gender gaps, but the relationship is weak, and the possibility that there really is no true relationship cannot be ruled out. A more nuanced answer comes from the multiple linear regression results. The multiple linear regression results tell the effect of National income controlling for Educational spending and Teachers per 100 students. Control variables are variables that are "held constant" in a multiple regression analysis in order to highlight the effect of a particular independent variable of interest. The multiple regression slope of 0.16 for National income means that every additional $1000 of National income is associated with an increase of 0.16 in a country's gender gap in science score, holding spending on education and the number of teachers in the country constant. This is different from the meaning of the 0.09 slope for National income in the simple linear regression model. Thinking of the slope in terms of predicted values, Model 1 predicts the gender gap using just National income. Countries that have higher incomes tend to have bigger gaps. But countries that have higher incomes also tend to have more spending on education and more teachers. When countries' incomes change, so do their spending and teacher levels. Predicting the gender gap for a rich country means predicting the gender gap for a country that spends a lot on education and has a lot of teachers. Since Educational spending and Teachers per 100 students aren't included in Model 1, the effect of National income includes the effects of everything that goes along with higher National income: bigger houses, better roads, more TV channels, nicer clothes -- and, of course, more Educational spending and more Teachers per 100 students. Model 4 predicts the gender gap using National income, Educational spending, and Teachers per 100 students all at the same time. In Model 4, higher National income still means bigger houses, better roads, more TV channels, and nicer clothes, but it doesn't mean more Educational spending or Teachers per 100 students. That's because Educational spending and Teachers per 100 students are "held constant" in making predictions using National income in Model 4. To see this, think about predicting the value of the gender gap. When all three independent variables are 0, the predicted gender gap is the intercept, 13.95 points. When National income goes up from $0 to $1000, the predicted gender gap is 13.95 + 1 x 0.16, or 14.11 points. When National income goes up to $2000, the predicted gender gap goes up another 0.16 points to 14.27 points. Every additional $1000 in income leads to another 0.16 point increase in the gender gap. What happened to Educational spending and Teachers per 100 students? They stayed at 0. They didn't change. The multiple linear regression slope of 0.16 for National income is the slope for National income considered independently of Educational spending and Teachers per 100 students. It is the slope for National income "holding constant" or "controlling for" Educational spending and Teachers per 100 students. The simple linear regression slope of 0.09 for National income is the slope for National income with any association between National income and the other two variables mixed in. The multiple regression in Model 4 examines the validity of the income theory of the gender gap independently of the spending theory and the teachers theory. There's nothing special about the order in which independent variables appear in regression models. The multiple linear regression in Model 4 also examines the validity of the spending theory independently of the income theory and the teachers theory, as well as the validity of the teachers theory independently of the income theory and the spending theory. Each variable is analytically equivalent, and regression results will be the same no matter what order the variables are entered. Why did the slope associated with National income go up between Model 1 and Model 4? There's no rule that regression slopes must go up or go down when control variables are used. The slope for National income went up because higher National incomes are usually associated with higher numbers of teachers. In Model 1, whenever National income goes up, Teachers per 100 students also tends to go up. National income has a positive effect on the gender gap, while Teachers per 100 students has a negative effect on the gender gap. So rising incomes tend to increase the gap, but the additional teachers associated with rising incomes tend to reduce the gap. The net result is a small increase in the gap (+0.09 points) for every $1000 increase in National income. It's a matter of two steps forward, one step back. In Model 4, the number of teachers is held constant. So is the level of Educational spending. As a result, Model 4 reveals the full impact of National income, which is +0.16 points for every $1000 increase in national income. The multiple linear regression slope for National income is larger than the simple linear regression slope because the other two variables are acting against the effect of National income. Controlling the other two variables unmasks the true explanatory power of National income. In effect, Educational sending and Teachers per 100 students complement Educational spending. Complementary controls are control variables that complement an independent variable of interest by unmasking its explanatory power in a multiple regression model. Complementary controls are highly desirable because they help clarify the true effects of independent variables on dependent variables. Independent variables don't always complement the other independent variables in a multiple regression model. In fact, they usually don't. Most of the time controlling for additional independent variables either has no effect on a model or reduces the strengths of the observed slopes in the model. For example, Figure 7-12 presents a reanalysis of the ODA spending regressions from Figure 7-5. Figure 7-12 starts with a simple linear regression of ODA spending on National income (Model 1), then adds in a control for Administrative costs (Model 2), then adds on an additional control for European status (Model 3). Controlling for Administrative costs has no effect on the slope for National income, while controlling for European status reduces the slope for National income.

Controlling for European status reduces the slope for National income because the variable European status competes with the variable National income in explaining levels of ODA spending across rich countries. Competing controls are control variables that compete with an independent variable of interest by splitting its explanatory power in a multiple regression model. From the standpoint of National income, European status is a competing control. On the other hand, from the standpoint of European status, National income is a competing control. They both compete to explain the same fact, that rich European countries have higher ODA spending than other countries. This was illustrated in Figure 7-5. The fact that the coefficient for National income remains significant in Model 3 while the coefficient for European status is not significant suggests that National income is the stronger of the two predictors of ODA spending. Any independent variable in a multiple regression model can be thought of as a control variable from the perspective of other independent variables. Whether or not a variable should be thought of as a control variable is up to the judgment of the researcher. If a variable is used with the intent that it should be held constant in order to bring out the true effect of another variable, it is a control variable. If a variable is of interest in its own right, then it is not. From a purely statistical standpoint, every independent variable in a multiple regression model is a control variable for all the other variables in the model. From a social science standpoint, a variable is a control variable if the researcher thinks it is, and if not, not.

7.4. Controlling for error (optional/advanced) Control variables are usually used to hold constant or control for one variable in trying to understand the true effect of another. Depending on the situation, the control variable might have no effect on the observed coefficient of the variable of interest, or it might complement or compete with the variable of interest. In all of these situations, the impact of the control variable is straightforward and easy to see: the observed slope for the variable of interest changes (or in the case of an ineffectual control variable, doesn't change) in response to the inclusion of the control variable. It may seem like these three possibilities (complement, compete, no effect) are the only possible effects of a control variable, but in fact there is one more way in which a control variable can affect a regression model. The control variable might reduce the amount of error in the model. Just such a situation is illustrated in Figure 7-13. Model 1 of Figure 7-13 repeats the regression of Canadian provincial smoking rates on average temperatures from Figure 4-8. Smoking rates fall with higher temperatures. Every 1 degree Fahrenheit increase in Temperature is associated with a 0.44% decline in smoking rates, and this result is highly significant statistically. Model 2 of Figure 7-13 takes the simple regression from Model 1 and adds a control for the Heavy drinking rate. Alcohol consumption is closely associated with smoking all across the rich countries of the world, including Canada (though, interestingly, in many poor countries it is not). Controlling for rates of Heavy drinking in Model 2 has no effect whatsoever on the slope for Temperature, which remains -0.44. It does, however, affect the standard error of the slope for Temperature.

In Model 1, the standard error of the slope for Temperature is 0.087, but the standard error declines to 0.062 in Model 2. The smaller standard error in Model 2 results in a larger t statistic. In this example, the effect of Temperature on the smoking rate is already highly significant (the probability that the true slope for Temperature is 0 is less than 0.001), so the higher t statistic doesn't change our interpretation of the model. Nonetheless, the slope for Temperature is more statistically significant in Model 2 than it is in Model 1. Why does the standard error of the slope go down when a control variable is introduced? Heavy drinking is completely unrelated to Temperature, but it is related to the smoking rate. In fact, Heavy drinking accounts for an important part of the total variability in smoking rates. As a result, there is less model error in Model 2 than in Model 1. Standard error is a function of the strength of the relationship between the independent variable and the dependent variable, the number of cases used to estimate the model, and the amount of error in the model. From Model 1 to Model 2 the strength of the relationship hasn't changed (it's still -0.44), the number of cases hasn't changed (it's still 13), and the amount of model error has declined (due to the effect of Heavy drinking). The net effect is that the standard error associated with Temperature has declined. Temperature is an even more significant predictor of smoking after controlling for Heavy drinking than it was before.

7.5. Case study: Child mortality in sub-Saharan Africa Out of every 1000 children born in Africa, only 850 live to their fifth birthdays. This mortality rate of 150 per 1000 children is shockingly high. By comparison, the child mortality rate in rich countries is typically around 5-6 per 1000 children. The United States has the highest child mortality rate in the developed world, with the loss of 7.7 out of 1000 children by age 5. Child mortality rates in African countries are typically 20 times as high. Child mortality and related statistics for 44 sub-Saharan African countries are reported in Figure 7-14. In addition to the metadata items, four variables are included: MORT -- The under-5 mortality rate per 1000 births INCOME -- National income per person in US Dollars FERT -- The fertility rate (mean births per woman of childbearing age) IMMUN -- The DPT (Diphtheria-Pertussis-Tetanus) childhood immunization rate A multicausal model of child mortality would predict that childhood mortality rates should decline with income (richer countries should have lower mortality), decline with immunization (countries with better immunization should have lower mortality), and rise with fertility (countries with more children should have higher mortality).

The results of three regression models to predict child mortality in sub-Saharan Africa are reported in Figure 7-15. Model 1 is a simple linear regression model with just one predictor, National income. Each additional $1000 of national income is associated with a decline in the child mortality rate of 6.84 children per 1000 children born in the country. This result is highly significant statistically.

Models 2 and 3 of Figure 7-15 are multiple linear regression models. Model 2 introduces the DPT immunization rate as a control variable. The inclusion of DPT immunization actually increases the size of the slope for National income from 6.84 to 8.49. This indicates that DPT immunization is complementary to national income. Counter-intuitively, immunization rates in Africa fall as national income rises, in part due to parental resistance to immunization in the richer African countries. As a result, controlling for immunization reveals an even stronger impact of National income in reducing child mortality rates. Model 3 introduces the Fertility rate as a control variable. Controlling for the Fertility rate dramatically reduces the size of the slope for National income. In fact, the slope for National income in Model 3 is not significantly different from 0. Fertility strongly competes with National income as an explanation of child mortality rates. It also competes with DPT immunization. The slope for DPT immunization is much smaller in Model 3 than in Model 2, but it is still statistically significant. How can child mortality be reduced in Africa? Obviously, higher incomes wouldn't hurt, but Model 3 suggests that immunization and family planning would be much more effective in reducing child mortality. That's good news, because social scientists know much more about ways to improve immunization and family planning than about ways to raise incomes. Model 3 suggests that rich countries' official development assistance (ODA) spending should focus on expanding immunization and family planning programs to support African families in their efforts to improve their children's health.

Chapter 7 Key Terms

Complementary controls are control variables that complement an independent variable of interest by unmasking its explanatory power in a multiple regression model.
Competing controls are control variables that compete with an independent variable of interest by splitting its explanatory power in a multiple regression model.
Control variables are variables that are "held constant" in a multiple regression analysis in order to highlight the effect of a particular independent variable of interest.
Multicausal models are statistical models that have one dependent variable but two or more independent variables.
Multiple linear regression models are statistical models in which expected values of the dependent variable are thought to rise or fall in a straight lines according to values of two or more independent variables.
Predictors are the independent variables in regression models.

← Chapter 6 · Chapter 8 →

Standardized Coefficients

We all know that when we drive, our cars pollute the atmosphere. We can literally see, feel, hear, and smell the pollution coming out of our exhaust pipes. Of course, cars aren't the only source of air pollution. Almost everything we do in modern society causes air pollution, and in particular the emission of carbon dioxide (CO2) into the atmosphere, which cases global warming. Shopping causes CO2 emissions because of all the energy used to get products into the stores in the first place. Sending an e-mail (CO2) emissions because of the electricity used by our computers. Eating causes CO2 emissions because of the electricity and gas used by our kitchen appliances. Even sleeping causes CO2 emissions if we use air conditioning or heating in our bedrooms, listen to music, or set an alarm clock. There's no way around it: simply living in modern society pollutes the air and contributes to global warming. In Chapter 3, countries' levels of CO2 emissions were regressed on their numbers of passenger cars in a simple linear regression model of CO2 emissions. Given that CO2 emissions come from multiple sources, not just passenger cars, it seems like a multicausal model would be more appropriate. Ideally, a multicausal model of CO2 emissions would include all sorts of variables, like electricity usage, air, rail, and truck transportation, agricultural CO2 emissions, and other sources of pollution. The inclusion of all of these variables in a multiple linear regression model would help create a model that might predict CO2 emissions very accurately, since all the contributors to CO2 emissions would be accounted for. A much simpler multicausal model of CO2 emissions is presented in Figure 8-1. Using data from Figure 3-1, tons of CO2 emissions per person in 51 countries are regressed on three predictors: passenger cars per 1000 people, national income per person, and western European status. Theoretically, greater numbers of passenger cars and higher overall national income per person should be associated with higher levels of CO2 emissions. Western European status should be associated with lower levels of CO2 emissions, since western European countries have been very active in promoting action on climate change in recent years. Three models are presented in Figure 8-1: a simple linear regression model based on passenger cars (Model 1), a multiple linear regression model that adds national income (Model 2), and an additional multiple linear regression model that also adds European status (Model 3).

From the perspective of passenger cars as an independent variable of interest, national income is a control variable. The slope associated with passenger cars is 0.013 in Model 1, but after controlling for national income the slope declines to 0.008. This decline means that national income is a competing control from the perspective of passenger cars: it competes with passenger cars in explaining the same facts about CO2 emissions. This is not surprising. After all, driving a car is an integral part of living life in a rich country. When countries have higher levels of national income per person, they have more cars. As a result, the two variables compete in explaining CO2 emissions in a country. For national income to complement passenger cars, it would have had to explain something else about a country that might have obscured the true relationship between passenger cars and CO2 emissions. Something that does complement both passenger cars and national income is European country status. European country status helps bring out the true relationships between passenger cars and CO2 emissions and between national income and CO2 emissions because European countries have relatively low emissions levels for their passenger car and national income levels. In western Europe, passenger cars tend to be small and fuel-efficient, so western European countries have lower levels of CO2 emissions for the same number of cars. Similarly, western Europe relies heavily on nuclear and wind power, resulting in lower CO2 emissions for the same level of national income. As a result, European status is a complementary control from the perspective of both passenger cars and national income. It complements national income especially strongly. Which variable has a stronger overall effect on CO2 emissions, the number of passenger cars or the level of national income more broadly? It's hard to say for sure, because the variables are expressed in very different units. An increase of one car per 1000 people has a smaller effect than an increase of $1000 in national income, but it's not obvious that this is a fair comparison. After all, an increase of 100 cars per 1000 people would have a much bigger effect than an increase of $1000 in national income. We could compare the t statistics for passenger cars and national income to determine which one is more significant statistically, but we don't yet have a mechanism for comparing the absolute sizes of the effects of different variables on the same scale. Without this, we can't determine which variable has a bigger impact on CO2 emissions. Going one step further, how much of the international variability in CO2 emissions is explained by these two variables taken together, or by these two variables plus European status? After all, the ultimate goal of statistical modeling is to explain things about the world. The models presented in Figure 8-1 partially explain country differences in CO2 emissions, but we don't know how much they explain CO2 emissions. This would be a very nice thing to know, certainly from a scientific standpoint but also from the standpoint of social policy. Politicians and the public have a legitimate desire to know just how much of the wide variability in the real world can be explained by our statistical models. If we can explain 90% of the observed variability in the world, great. If we can explain 50%, alright, at least that's something. If we can only explain 10% of the observed variability in the world and the rest of reality is fundamentally random, the world has a legitimate right to ignore us and our statistical results.

This chapter shows how the relative explanatory power of different variables can be directly compared in the context of multiple regression models. First, in order to compare variables, they have to be put on the same scale through a process called standardization (Section 8.1). Regression slopes estimated using standardized variables can be used to directly compare the relative explanatory power of each variable. Second, when standardized variables are used in a simple linear regression the result is a correlation coefficient that measures the strength of the relationship between the variables (Section 8.2). The correlation conveniently measure the strength of the relationship between two variables on a scale from -1 to +1. Correlation coefficients can also be used to evaluate the overall predictive power of any regression model (Section 8.3). The total variability in the dependent variable that is explained by the independent variables can also be measured. An optional section (Section 8.4) illustrates how correlation coefficients can be used to explore the structure of the relationships connecting a large number of variables at the same time. Finally, this chapter ends with an applied case study of people's satisfaction with democracy in Taiwan (Section 8.5). This case study illustrates how standardized regression coefficients are used to evaluate and compare the performance of different variables in multiple regression models. It also illustrates how the relative explanatory power of different regression models can be compared. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should be able to use multiple regression to make basic inferences about the effects of multiple independent variables on a single dependent variable.

8.1. Comparing like with like using standardized variables Linear regression involves comparing the values of variables that mean very different things. In Model 2 of Figure 8-1 it is reported that every 1 additional passenger car per 1000 people in a country is associated with an increase of 0.008 tons of CO2 emissions per person, while every $1000 in national income is associated with an increase of 0.074 tons of CO2 emissions. The variable passenger cars is expressed as a number per 1000 people, the variable national income is expressed in thousands of dollars, and the variable CO2 emissions is expressed as tons per person per year. The use of so many different units makes it hard to compare countries across different variables. For example, Australia has 542 cars per 1000 people, a national income of $29,480 per person, and CO2 emissions of 18.1 tons per person. Are these figures high, low, or about average? How do they compare to each other, and to other countries? One way to judge whether a value of a variable is high or low is by using means and standard deviations. Figure 8-2 reports the means and standard deviations of CO2 emissions, passenger cars, and national income for the 51 countries used in Figure 8-1. Australia's CO2 emissions (18.1 tons) are well above the mean level for CO2 emissions across the 51 countries. In fact, Australia's CO2 emissions are more than 2 standard deviations above the mean. The mean is 6.15 tons. The mean plus one standard deviation is 6.15 + 4.34 = 10.49 tons. The mean plus two standard deviations is 6.15 + 4.34 + 4.34 = 14.83 tons. Australia, with emissions of 18.1 tons, is far above this level.

Australia also has a large number of cars per 1000 people, 542 cars versus a cross-national mean of 242 cars. Australia's level is more than 1 standard deviation above the mean, but not quite 2 standard deviations. Australia's national income level of $29,480 is well above the mean, but by a little less than 1 standard deviation. It's actually just 0.83 standard deviations above the mean. So while Australia is around 1 standard deviations above the mean on passenger cars and national income, it's more than 2 standard deviations above the mean on CO2 emissions. This suggests that CO2 emissions are especially high in Australia. Looking back at Figure 3-2, this seems to be the case: Australia's observed CO2 emissions are much higher than its expected levels as indicated by the regression line. Australia is a clear outlier. On the other hand, Mexico is 0.47 standard deviations below the mean on CO2 emissions, 0.51 standard deviations below the mean on passenger cars, and 0.42 standard deviations below the mean on income. It is below the mean by roughly the same amount on all three variables. It is also much closer the mean on all three variables than Australia is, at least in terms of standard deviations. For example, where Mexico is 0.47 standard deviations below the mean on CO2 emissions, Australia is 2.75 standard deviations above the mean. Discussing variables in terms of standard deviations above or below the mean is actually a very useful technique. Instead of computing standard deviations above or below the mean for particular cases, it makes more sense to convert all the values of a variable into standard deviations above or below the mean at the same time in a process called "standardization." Standardized variables are variables that have been transformed by subtracting the mean from every observed value and then dividing by the standard deviation. Because of the way they are constructed, standardized variables always have a mean of 0 and a standard deviation of 1. Also because of the way they are constructed, standardized variables have no units. For example, Mexico is 0.42 standard deviations below the mean on national income. It is not 0.42 dollars below the mean or 0.42 percent below the mean. It is just 0.42 standard deviations below the mean. This is the only downside of standardized variables: they have no units. When social statisticians are interested in doing something that requires the original units, like using a regression model to make predictions, they need the original units. Unstandardized variables are variables that are expressed in their original units. All variables start out as unstandardized variables, expressed in dollars, pounds, percentages, cars per 1000 people, or some other unit. In general, "unstandardized variables" are just "variables." The term "unstandardized variable" is only used to when it is necessary to distinguish an unstandardized variable from a standardized variable. The most important use of standardized variables is in linear regression models. In Figure 7-13, smoking rates in the 13 Canadian provinces and territories were regressed on average daily temperatures and rates of heavy alcohol drinking. Both temperature and heavy drinking were statistically significant predictors of smoking rates, but since they are recorded in different units (degrees versus percents) their effects were difficult to compare. Standardizing all three variables (smoking, temperature, and drinking) makes possible a meaningful comparison of the effects of temperature and drinking on smoking rates. The first step in standardizing variables is to find their means and standard deviations. Means and standard deviations for all three variables are reported in Figure 8-3. The second step is to use these means and standard deviations to convert each value of each variable into a standardized value.

Normally, standardization is performed automatically by statistical computer software, but the steps in the process of standardization are illustrated in Figure 8-4 for the variable "heavy drinking." All 13 Canadian provinces and territories are listed in Column 1 and their heavy drinking rates are reported in Column 2. The mean value of heavy drinking is recorded in Column 3. The difference between each value and the mean is calculated in Column 4. The standard deviation of heavy drinking is recorded in Column 5. The standardized value of heavy drinking for each province is calculated in Column 6. The values in Column 6 represent how many standard deviations each province is from the mean level of heavy drinking for all provinces.

Standardization changes the value of each case in a variable into a standardized value, but it does not change the distribution of a variable in any way. High cases are still high cases and low cases are still low cases. It's only the units that change. This is illustrated in Figure 8-5. The left side of Figure 8-5 is a scatter plot of smoking rates versus heavy drinking rates for the 13 Canadian provinces and territories using the original, unstandardized variables. The right side of Figure 8-5 depicts the same relationship using standardized variables. The layout of the points is identical, but the scales of the axes change. The standardized plot is centered on 0 and runs from a low of -3 to a high of +3 in each direction. Notice also how the regression line depicted on the standardized plot runs right through the center point. This happens with any regression estimated using standardized variables.

The coefficients of a multiple linear regression model regressing the provincial smoking rates on average temperatures and heavy drinking rates are reported in Figure 8-6. Two sets of coefficients are reported, one set using the unstandardized variables and one using the standardized variables. Unstandardized coefficients are the coefficients of regression models that have been estimated using original unstandardized variables. Standardized coefficients are the coefficients of regression models that have been estimated using standardized variables. The unstandardized coefficients are just the regular coefficients found using the three variables in their original units. They are the same as the coefficients that were reported in Figure 7-13, Model 2. The standardized coefficients, on the other hand, are the coefficients of the model that result when the new, standardized versions of the variables are used.

Since the standardized coefficients are both expressed in standardized units (in terms of standard deviations, not degrees or percentages), they are directly comparable. The relationship between temperature and smoking is more than twice as strong as the relationship between heavy drinking and smoking. Every one standard deviation increase in temperature is associated with a 0.832 standard deviation decline in the smoking rate, while every one standard deviation increase in heavy drinking is associated with a 0.398 standard deviation increase in the smoking rate. No intercept is reported for the standardized model because the intercept for standardized models is always 0. It would not be incorrect to report 0 as the intercept, but it is customary to leave the intercept blank for standardized models. Because of this custom, it is easy to tell at a glance whether a model uses unstandardized or standardized variables. Whenever an intercept is reported, the model is unstandardized. When no intercept is reported, the model must be standardized. The t statistics and probability levels are the same for the unstandardized and standardized coefficients. Since standardization doesn't change anything about the layout of the points in an analysis or the amount of error, it doesn't have any effect on significance levels. The standardized coefficients for the regressions models for CO2 emissions are reported in Figure 8-7. In Model 2, the standardized coefficient for passenger cars is larger than the standardized coefficient for national income. This indicates that the number of passenger cars predicts CO2 emissions more strongly than does the level of national income. The difference between the two standardized coefficients is small but clear. Controlling for western European status in Model 3 changes the situation. In Model 3, the standardized coefficient for national income is stronger than the coefficient for passenger cars. This happens because controlling for western European status removes a lot of the error from the relationship between national income and CO2 emissions (western European status strongly complements national income).

So which variable most strongly predicts CO2 emissions? The answer is that their effects are about equal. Which one is stronger depends on whether or not we control for western European status. Western European status itself has a much weaker effect on CO2 emissions, a little more than half as strong as either of the other variables. The use of standardized variables to produce standardized coefficients makes all these comparisons possible.

8.2. Correlation In Figure 8-6 and Figure 8-7, standardized coefficients are used to compare the relative strengths of relationships within a model. The relationship between temperature and the smoking rate is much stronger than the relationship between heavy drinking and the smoking rate across Canadian provinces. The relationship between passenger cars and CO2 emissions is roughly the same strength as the relationship between national income and CO2 emissions across countries. In each of these cases, the strengths of different relationships are compared within a single regression model. Standardized coefficients can also be used to compare the strengths of relationships across models. For example, in Chapter 1 it was theorized that low incomes led to higher junk food consumption. This theory was operationalized into two specific hypotheses. First, it was hypothesized that US states with higher median incomes would have less soda consumption. Second, it was hypothesized that states with higher incomes would have less sweetened snack consumption. It turned out that the first hypothesis was correct, but the second was wrong. Contrary to expectations, states with higher incomes actually had more sweetened snack consumption, not less. We might want to know which relationship was stronger, the (expected) relationship between income and soda or the (unexpected) relationship between income and sweetened snacks. The results of regressions of each dependent variable on state median income are reported in Figure 8-8 and Figure 8-9. The unstandardized coefficients in each model are the same coefficients as were reported in Chapter 1. The unstandardized coefficients indicate that each additional $1000 in state median income is associated with a 0.603 gallon decline in soda consumption per person per year and a 0.611 pound increase in sweetened snack consumption per person per year. The standardized coefficients indicate that the strength of the relationship between income and soda consumptions is actually slightly stronger than the strength of the relationship between income and sweetened snack consumption.

Figure 8-8. Comparison of metric and standardized coefficients for regression of soda consumption on state median income for 48 US states, 2008 (data from Figure 1-2)

Figure 8-9. Comparison of metric and standardized coefficients for regression of sweetened snack consumption on state median income for 48 US states, 2008 (data from Figure 1-2)

Standardized coefficients from simple linear regression models are often used in this way to gage the strengths of the relationships between variables. Standardized coefficients are a convenient shorthand for the relationship between two variables for several reasons. First, since they are based on standardized variables, they are always comparable, no matter what units the original variables were measured in. Second, it turns out that in simple linear regression models with one predictor, it doesn't matter which variable is the dependent variable and which is the independent variable. Either way the standardized coefficient will be the same. Third, again only in simple linear regression models with one predictor, it turns out that the standardized coefficient will always fall somewhere between -1 and +1. The slope is never larger than 1 in either direction. This use of standardized coefficients from simple regression models is so common that it has its own name and symbol: correlation, denoted using the symbol "r." Correlation (r) is a measure of the strength of the relationship between two variables that runs from r = -1 (perfect negative correlation) through r = 0 (no correlation) to r = +1 (perfect positive correlation). The correlation between two variables is exactly the same thing as the standardized coefficient from a regression of one of the variables on the other variable. Figure 8-10 demonstrates how the correlations of state income with soda and sweetened snacks might be compared. Notice how the correlation coefficients are identical to the simple linear regression coefficients reported in Figure 8-8 and Figure 8-9. Similarly, their probabilities correspond to those from the t statistics reported in Figure 8-8 and Figure 8-9.

Figure 8-10. Correlation of state median income with soda and sweetened snack consumption for 48 US states, 2008

8.3. R and R2 In addition to gaging the strengths of the relationships between variables in general, correlations have another, very specific use. Correlations can be used to evaluate the overall predictive strength of any regression model. For example, the table in Figure 8-11 repeats the results of the regression of the gender gap in science scores on three independent variables (national income, educational spending, and number of teachers) from Figure 7-6. In Figure 8-11 both unstandardized and standardized coefficients are reported. The standardized coefficients indicate that the effects of teachers and national income are stronger than the effects of educational spending, but they don't tell us how well the model as a whole does in predicting the gender gap in science.

Correlations can be used to help shed light on this. The key question in evaluating the performance of a model is: how well do the values of the dependent variable predicted by the model correspond to the actually observed values of the dependent variable? In other words, what is the strength of the relationship between the dependent variable's expected values and its actual values? A correlation is ideal for measuring the strength of the relationship between two variables. When the two variables being correlated are the actual and expected values of a dependent variable from a regression model, the correlation is represented by the capital letter R (to distinguish it as a specific type of correlation). For Model 1 of Figure 8-11, R is 0.446. This means that in Model 1 of Figure 8-11 the actual values of the gender gap in science are correlated r = 0.446 with the expected values generated by the regression model. This is not ideal (a perfect correlation would be r = 1), but it's something. Figure 8-12 plots the actual values of the gender gap in science scores against the expected values generated by Model 1 of Figure 8-11. There is a definite positive relationship between the two, but it is not very strong. By way of comparison, for the regression predicting smoking rates across Canadian provinces (Figure 8-6) the model's predictive performance was R = 0.928, while for the regression predicting CO2 emissions across countries (Model 3 of Figure 8-7) the model's predictive performance was R = 0.632. The regression model in Figure 8-11 does predict the gender gap in science scores, but not especially well.

In addition to summarizing the predictive strength of a regression model, the regression model R statistic also has one more very important use. The R statistic plays a role in linking regression models back to mean models. In Chapter 4, Figure 4-10 showed how the mean model for smoking rates across Canadian provinces could be mapped into the regression model for smoking. Each province's deviation from the mean smoking rate (left side of Figure 4-10) was spread out over the range of average temperatures in the regression model for smoking (right side of Figure 4-10). In Figure 8-13, the same kind of mapping is done for the relationship between smoking rates and heavy drinking rates. Again, each province's deviation from the mean smoking rate (left side) is spread out over the range of the independent variable, which in this case is heavy drinking (right side).

Viewed in this way, a regression model is nothing more than an explanation of why certain cases deviate from the mean more than other cases do. In this view, Ontario has a low smoking rate at least in part because it has a low drinking rate, while the Northwest Territories have a high smoking rate at least in part because they have a high drinking rate. These provinces' smoking rates are also explained in part by their temperatures (Figure 4-10). Together, temperatures and heavy drinking rates explain a large portion of the total cross-province variability in smoking rates, but how much? Answering this question properly requires a lot of algebra, but the end result of all that algebra is that the proportion of the total variability in the dependent variable that is explained by the independent variables in a regression model is equal to R x R, or R2 ("R squared"). R2 is a measure of the proportion of the total variability in the dependent variable that is explained by a regression model. As with other regression-related statistics, there is no need to calculate R2. Any software program that estimates regression models will automatically report the R2 statistic for the model. The R2 for the model predicting the gender gap in science scores in Figure 8-11 is 0.199 or 19.9%, indicating that together national income, educational spending, and the number of teachers in a country explain almost 20% of the international variability in the gender gap in science. The R2 for the model predicting Canadian provincial smoking rates (Figure 8-6) is 0.861, indicating that over 86% of the variation across provinces in smoking rates can be explained by differences in temperatures and heavy drinking. The R2 for the full model predicting CO2 emissions across countries (Model 3 of Figure 8-7) is 0.399, indicating that nearly 40% of international differences in CO2 emissions are explained by differences in national income, passenger cars, and western European status. Since R2 has such an important intuitive meaning (proportion of variability explained), most tables of regression results report R2, not R. Since by definition R2 equals R squared, it is easy to calculate one from the other (if necessary) using a calculator. In practice, R is rarely used, but R2 is reported and discussed for almost every regression model.

8.4. Correlation matrices (optional/advanced) Correlations are summary measures of the strengths of the relationships between variables. As such, they are useful even outside the context of regression models. Sometimes we just want to know what relationships exist among a group of variables. A table of all the correlations connecting a group of variables is called a correlation matrix. For example, the correlation matrix for the four variables included in Figure 8-6 (the regression model for CO2 emissions) are reported in Figure 8-14. The dependent variable from the regression model is listed first in Figure 8-14, followed by all the independent variables, but the order of variables in a correlation matrix doesn't have any effect on the correlations. The table or matrix is just a convenient way to organize all the correlations among all the variables.

Correlations matrices like the one depicted in Figure 8-14 always have the same number of rows as columns, because every variable is listed both as a row and as a column. Where a variable is matched with itself in the table, the correlation is always 1 (every variable is perfectly correlated with itself). As a result, correlations matrices always have a diagonal of 1's running through the middle. Another feature of correlation matrices is that the correlations reported in the upper right corner are the mirror image of the correlations reported in the lower left corner. This happens because correlations are symmetrical: the correlation of income with cars is the same as the correlation of cars with income. Since the entries in the upper right corner repeat the entries in the lower left corner, the upper right corner is sometimes left blank in correlation matrices. These half-blank matrices with the redundant correlations removed are known as triangular matrices. A triangular correlation matrix with seven variables is depicted in Figure 8-15. These correlations are based on the characteristics of 1145 Taiwanese respondents to the 2006 World Values Survey (to be discussed in Section 8.5). Due to the long names of some of the variables, each variable is listed on a numbered row, and the numbers are used as headings for the columns. Means and standard deviations for all of the variables have also been included for easy reference. Correlations matrices with means and standard deviations summarize all of the important features of a group of variables in a compact space. Though many authors do use triangular matrices like the one depicted in Figure 8-15, full (square) matrices are much more convenient. It can take a few minutes to find the correlation you're looking for in a triangular matrix, but in a square matrix you can always read across a row to find any correlation you want.

Correlation matrices can be used both to pick out which independent variables are likely to be significantly related to the dependent variable. For example, in Figure 8-15 the variables that are most closely related to the democracy rating are age, education, and confidence in institutions. Correlations matrices can also be used to pick out which independent variables are likely to compete with or complement each other based on what independent variables are correlated with each other. Highly correlated groups of variables like age, education, and income, or trust and confidence, are likely to compete with or complement each other. Variables that are not correlated with each other are unlikely to be either competing or complementary when used in a regression model. Differentiating between competing and complementary controls based on the correlation matrix, however, is difficult or impossible.

8.5. Case study: Satisfaction with Taiwan's democracy In Chapter 5, data from the Taiwan edition of the 2006 World Values Survey (WVS) were used to study the relationship between people's ages and their ratings of the quality of democracy in Taiwan. People's rating of democracy in Taiwan was scored on a scale from 0 to 100 where: Rating = 0 means the respondent thinks there is not enough democracy in Taiwan Rating = 50 means the respondent thinks there is just the right amount of democracy in Taiwan Rating = 100 means the respondent thinks there is too much democracy in Taiwan In a regression model reported in Figure 5-7, age was found to be positively related to people's rating of Taiwan's democracy, with each additional year of age predicting a 0.105 point increase in the democracy rating (older people thought Taiwan was more democratic than younger people). The mean democracy rating among the 1216 people studied was 38.7, indicating the most people were less than satisfied with the amount of democracy in Taiwan. The results of two more extensive multiple regression models for the democracy rating in Taiwan are reported in Figure 8-16. These models are based on only 1145 survey responses because some people didn't answer all of the questions used in the models. The models reported in Figure 8-16 include six independent variables: Age -- the respondent's age in years Gender -- the respondent's gender, coded as Female=0 and Male=1 Education -- the respondent's yeas of education Income -- the respondent's income decile (lowest tenth, second tenth, third tenth, etc.) Trust in society -- a variable measuring the respondent's level of trust in society on a scale from 0 to 18 Confidence in institutions -- a variable measuring the respondent's level of confidence in the institutions of society (like government, corporations, and churches) on a scale from 0 to 45 It is expected that education and income would be positively related to people's ratings of democracy, since people who have been more successful at advancing in society usually have a higher opinions of that society. Similarly, those who have a higher level of trust and confidence in their society's institutions would be expected to rate their society's democracy more highly. Gender is also included as a control variable, but with no particular expectation of its effects.

The first column of results in Figure 8-16 reports the correlations of the democracy rating with each of the six independent variables. Only three of these correlations are statistically significant: those for age, education, and confidence in institutions. Figure 8-16 also reports the results of two regression models. For each model, both unstandardized coefficients and standardized coefficients are reported. The unstandardized coefficients are just the ordinary regression coefficients based on the unstandardized variables for each of the variables in the model. The standardized coefficients are the regression coefficients that result from the same regression model estimated using standardized variables. The standardized coefficients in Model 1 indicate that age has the most powerful effect on the democracy rating of any of the four variables included in the model. In Model 2, confidence in the institutions of society (including government) is positively associated with people's ratings of their country's democracy. This makes sense, since people who have no confidence in government would be unlikely to rate their government as being very democratic. Surprisingly, trust in society has no significant effect on people's ratings of how democratic their government is in Taiwan. The R2 statistics for both models are shockingly low. The R2 of 0.019 for Model 1 indicates that the variables in Model 1 altogether explain only 1.9% of the total variability in people's ratings of Taiwan's democracy. The R2 rises as variables are added in Model 2, but at 0.026 (2.6%) it is still very low. These low R2 scores call into question the substantive significance of the two models. Both models have statistically significant coefficients, but a model that explains less than 3% of the total variability in the dependent variable may not be very useful from a policy standpoint. The real reasons behind people's ratings of the level of democracy of their own government remain a mystery, at least in Taiwan.

Chapter 8 Key Terms

Correlation (r) is a measure of the strength of the relationship between two variables that runs from r = −1 (perfect negative correlation) through r = 0 (no correlation) to r = +1 (perfect positive correlation).
R2 is a measure of the proportion of the total variability in the dependent variable that is explained by a regression model.
Standardized coefficients are the coefficients of regression models that have been estimated using standardized variables.
Standardized variables are variables that have been transformed by subtracting the mean from every observed value and then dividing by the standard deviation.
Unstandardized coefficients are the coefficients of regression models that have been estimated using original unstandardized variables.
Unstandardized variables are variables that are expressed in their original units.

Regression Model Design

Many people worry that modern society is alienating. Alienation means that people feel disconnected from larger society. Alienation was one of the first problems studied by the sociologists who founded the discipline in the late 19th century, and it continues to be a major concern today. A major symptom of alienation is a lack of trust in society. In small, closed communities where everyone knows everyone else, people have the opportunity to develop trusting relationships over years of mutual interaction. In modern societies, people end up being strangers to the people around them in stores and restaurants, their neighbors, and even their extended families. People still have friends, but their friends are spread out in wide networks. The era of village societies when you were likely to marry your next-door neighbor disappeared long ago. Nonetheless, trust is extremely important for the functioning of modern society, especially in democratic countries. If people don't have trust in society, they won't help their neighbors in times of need, enter into long-term contracts like university degree programs, or participate in democratic elections. At the most basic level, trust in society is necessary for society to function at all. Without it, we're all on our own. The World Values Survey (WVS), conducted in more than 80 countries, includes six questions about trust in society. They are: How much do you trust your family? How much do you trust people in your neighborhood? How much do you trust people you know personally? How much do you trust people you meet for the first time? How much do you trust people of another religion? How much do you trust people of another nationality? Each question can be answered on four levels, ranging from 0 = "No trust at all" through 3 = "Trust completely." An index of overall trust in society can be calculated by adding together each respondent's answers to all six questions. This index, "Trust in society," then ranges from a possible low score of 0 (the respondent answers "No trust at all" on all six questions) to 18 (the respondent answers "Trust completely" on all six questions). Of course, most people fall somewhere in the middle. Using data from the United Kingdom edition of the 2006 World Values Survey (WVS), the mean level of trust in society was 12.5 with a standard deviation of 2.4. Most people in the United Kingdom have a high level of trust in society. The full distribution of trust in society in the United Kingdom is plotted in Figure 9-1.

While most people in the United Kingdom have high levels of trust in society, there are still may people who don't. Regression models could be used to help us understand why. First off, we might expect that many of the differences between people in their levels of trust in society would be determined by basic demographic factors: who they are, where they live, and how they were brought up. These should certainly be included in any model as control variables. Since trust in society includes trust in your family and in people of other religions, we might also control for family and religious factors. People's levels of trust in society might also be determined in part by differences in the ways people of different social statuses experience society. A regression of trust in society on social status should show a positive, statistically significant effect of social status. People of high social status should show significantly more trust in society because society has, in general, been good to them, while people of low social status should show less trust in society. Using WVS data, ten variables have been selected to use in studying differences in trust in society. Seven of them are background variables and three are alternative operationalizations of social status. The ten variables are: Gender -- the respondent's gender, coded as Female=0 and Male=1 Age -- the respondent's age in years Size of city or town -- population of the respondent's city of residence, scaled from 1 = less than 2000 people to 8 = greater than 800,000 people Marital status -- whether or not the respondent is married (Married=1) Parental status -- whether or not the respondent is a parent (Yes=1) Religiosity -- coded on a ten-point scale from 1 = "religion is not at all important in my life" to 10 = "religion is very important in my life" Race -- white (1) versus non-white (0) Education -- the respondent's yeas of education Income -- the respondent's income decile (lowest tenth, second tenth, third tenth, etc.) Supervisory position -- the respondent supervises other people at work (Yes=1) The results of a series of regression models using these ten independent variables to predict trust in society are reported in Figure 9-2. The first column in Figure 9-2 reports the correlation of each variable with trust in society. The remaining columns report the regression results. All of the coefficients are standardized so that the effects of the three different social status indicators can be compared. The original, unstandardized variables for education, income, and supervisory position are all measured on different scales, so their unstandardized coefficients would not have been directly comparable. The significance level for each coefficient is marked with an appropriate symbol, and the R2 for each model is reported at the bottom of each column. The R2 scores indicate that the models explained anywhere from 5.5% to 9.3% of the total variability in trust in society in the United Kingdom.

Model 1 includes all the background factors together in a single regression model. Interestingly, marriage and parenting seem to complement each other. Neither marital status nor parental status is significantly correlated with trust in society, but in the regression model both variables are significant when controlling for the other. Model 2 also includes all of the background factors, but adds education, which is highly significantly related to trust in society. In Model 3, income is found to be highly significantly related to trust in society, but in Model 4 the effect of holding a supervisory position at work is non-significant. In the final model, Model 5, the only social status variable that has a highly significant coefficient is education. The fact that the coefficients of all three social status variables are smaller in Model 5 than in the other models indicates that these three variables compete with each other in explaining trust in society. This would be expected, since they are all different ways of operationalizing the same concept. People who are highly educated tend to have high incomes and supervise other people at work, while people who are poorly educated tend to have low incomes and not supervise other people at work. Since the (standardized) coefficient for education in Model 5 is much larger than the (standardized) coefficients for income and supervisory position, we can conclude that education is the most important of the three social status determinants of trust in society. Which of the five models is the best model for explaining how social status affects trust in society? That depends on just what it is that the researcher wants to know about the effects of social status. All of the models add information that might be useful. A fuller picture of the determinants of trust in society can be developed using all five models than from any one of the models by itself.

This chapter examines in greater detail how independent variables are selected for inclusion in multiple regression models. First, background control variables that are not particularly of theoretical interest in an analysis are often lumped together in an initial base model (Section 9.1). The selection of variables to include in a base model depends on the kinds of cases being used: individual people, whole countries, or something in between. Second, the proper selection and layout of variables in regression analyses depend on the purposes for which the results of the models will be used (Section 9.2). The main distinction is between whether the models will be used for prediction or for explanation. Third, the concepts of competing and complementary controls can help make sense of some of the many reasons for including control variables in models (Section 9.3). Six reasons are highlighted, though other reasons are possible. An optional section (Section 9.4) focuses on the problems that can arise when a single model contains two or more variables that operationalize the same concept. Finally, this chapter ends with an applied case study of the gender gap in wages in the United States (Section 9.5). This case study illustrates how regression models can be designed to help shed light on an important topic in social policy. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should have a more sophisticated understanding of how independent variables are selected for and used in regression models.

9.1. The base model Compared to the models used so far in this book, models like those reported in Figure 8-16 and 9-2 have a large number of independent variables. Most regression models used by social scientists include many independent variables, from 6 or 8 up to sometimes 20 or more. When models include so many variables, it is necessary to have some way to organize them. A good place to start is with a base model. Base models are initial models that include all of the background independent variables in an analysis that are not of particular theoretical interest for a regression analysis. For example, in studying the relationship between social status and trust in society, variables like gender, age, town size, and all the other variables included in Model 1 of Figure 9-2 are not of particular theoretical interest. They are only included in order to control for the backgrounds of the people in the study. Model 1 would be considered a base model for Figure 9.2. The kinds of variables that are typically used in base models for different kinds of data are summarized in Figure 9-3. The variables to be included in a base model often depend simply on what data are available. For databases where the cases are individuals, many different variables are usually available. As you move up the chain to larger and larger units, less and less data are available, and so fewer and fewer base model variables tend to be included. For models comparing countries, the one variable that is almost always included is national income per person. The inclusion of national income in regression analysis helps adjust for the fact that rich countries like the United States and Japan are different in almost every way from poor countries like Cambodia and Haiti. If a researcher using cross-national data didn't control for national income, people who disagrees with the researcher's views would almost certainly raise this as a major criticism of the researcher's regression models.

The main purpose of base models is usually to make cases equivalent for comparison. In the data underlying Figure 9.2, the respondents range in age from 16 to 89 years old. Some are British born and bred for generations, while others are recent migrants from Jamaica or Pakistan. Of course, some are men and some are women. They are an incredibly diverse group of people who have had very different experiences of society. Controlling for these background factors allows us to compare like with like. Because age is included as a control variable in the analyses, we can make statements like these about Model 2: Holding age constant, the relationship between education and trust in society is significant. For any given age, education has a significant effect on trust in society. The age-adjusted relationship between education and trust in society is significant. The relationship between education and trust in society is significant net of age. These are all different ways of expressing verbally the fact that we have controlled for age. In mathematical terms, part of the difference in trust levels between people of different ages has been attributed to age, while another part has been attributed to education (and other variables). An important function of the base model is to control for basic background variables that are likely to be confounded with the explanatory variables of interest in an analysis. Confounding variables are variables that might affect both the dependent variable and an independent variable of interest. So, for example, age affects trust in society (the correlation of r = 0.162 is the strongest for any of the 10 variables in Figure 9.2), but it also affects social status. Your own education level can only go up as you get older, but at any one time for society as a whole older people are less educated, because people used to spend fewer years in school than they do today. It turns out that among the 567 United Kingdom WVS respondents used in Figure 9-2, the correlation between age and education is r = -0.218. Since older people have lower education and higher trust in society, age is a confounding variable in the analysis of the relationship between education and trust. If regression analyses usually start out with a base model, they usually end with a saturated model. Saturated models are final models that include all of the variables used in a series of models in an analysis. Model 5 in Figure 9-2 is an example of a saturated model. Saturated models can sometime be difficult to interpret because of the large numbers of variables used, but they are almost always included for completeness.

9.2. Explanatory versus predictive models In between the base model and the saturated model, there are no real rules about what variables should be included in regression models or in what order. A common approach is to do what's been done in Figure 9-2: start with the base model, then add the independent variables of interest one at a time in separate models, then report a saturated model in which all of the independent variables are used at the same time. When models are designed to evaluate the relative strengths of different explanations of the dependent variable, the independent variables have to be entered one at a time in separate models. This makes it possible to compare how well each of them explains the dependent variable. Explanatory models are regression models that are primarily intended to be used for evaluating different theories for explaining the differences between cases in their values of the dependent variable. On the other hand, sometimes the objective of a regression analysis is simply to predict the values of a dependent variable, without any interest in the theoretical implications of the models. Predictive models are regression models that are primarily intended to be used for making predictions about dependent variables as outcomes. For example, in Figure 3-9 a very simple predictive model was used to predict levels of soft drink consumption in the US states of Alaska and Hawaii. In predictive models, it is less important to understand how the coefficients of variables change between models or to control for potentially confounding variables. All that really matters is getting a high R2 score, since R2 indicates the proportion of the total variability in the dependent variable that is accounted for by the model. In general, models with higher R2 scores make more accurate predictions of the dependent variable. Some of the key differences between explanatory models and predictive models are laid out in Figure 9-4. A major difference is the way that independent variables are selected for inclusion in each model type. The main objective of an explanatory model is to make inferences about the effects of different independent variables on the dependent variable. Independent variables are carefully selected for inclusion based on specific theoretical reasons, and unimportant or irrelevant variables are never included. Keeping the number of independent variables to a minimum also makes it easier to understand the role each one plays in explaining the dependent variable. In other words, explanatory models place a premium on parsimony. Parsimony is the virtue of using simple models that are easy to understand and interpret. A good explanatory model is one that sheds light on relationships that are of theoretical interest. In contrast, predictive models often take much more of a wild-west, anything-goes approach. So long as the independent variables are correlated with the dependent variable, they help in making predictions. A bizarre example of this is the use of sewage treatment flows in so-called "toilet flush models" of hotel occupancy rates. In beach resort areas, city managers want to know how many visitors they have over a major holiday weekend, but there is no single database that includes a list of all the people who stay in a city's hotels, in private rentals, or visiting friends and relatives. Instead, city managers use the amount of sewage flowing through their sewage treatment plants over the weekend to estimate the number of people who must have been in the city. There's no theoretical sense in which sewage causes people to visit a city, but sewage is a very good predictor of the number of people who actually have visited.

9.3. Reasons for controlling in explanatory models A major challenge in designing regression models is deciding just what to control for. In predictive models, the decision is easy: if a variable is available for use and it helps predict the dependent variable, use it. In explanatory models, the decision is much harder. There are at least six reasons why control variables might be used in an explanatory model, though others are possible as well. They are: A. To eliminate alternative explanations B. To compare the power of different explanations C. To hold constant a competing explanation D. To make cases equivalent for comparison E. To reduce model error F. To bring out effects that were hidden by error The first three reasons (A-C) mainly apply in cases where the control variable tends to compete with other independent variables in explaining the dependent variable. In such cases, the use of the control variable tends to reduce the size and statistical significance of the effects of the other independent variables. The last three reasons (D-F) mainly apply in cases where the control variable tends to complement the other independent variables. In such cases, the use of the control variable can actually increase the size and significance of the effects of the other independent variables. The six reasons and explanations of the kinds of situations in which they are used are summarized in Figure 9-5.

All six reasons for using control variables can be illustrated using a series of regression models that are designed to shed light on the reasons why some countries are more successful than others at immunizing their children against common infections. Though there are some controversies surrounding its use, the combined diphtheria-pertussis-tetanus (DPT) vaccine is widely used around the world to immunize infants between 12 and 23 months old against three potentially deadly childhood diseases. The World Health Organization and most national health authorities have official DPT immunization programs. Nonetheless, DPT immunization rates vary from under 40% in some of the poorest countries of Africa to over 98% in many of the middle-income countries of the middle east and eastern Europe. The DPT immunization rate is not a major policy issue in rich countries, both because immunization rates are usually over 90% and because the three diseases -- diphtheria, pertussis, and tetanus -- are not generally life threatening in countries with good medical systems. On the other hand, in poor countries DPT immunization can literally be a matter of life and death for young children. From a policy standpoint, we would like to understand why DPT immunization programs are more successful in some countries than in others, especially in poor countries. Several explanations are possible. First, in many rich countries DPT immunization rates fall well below their potential because of parental concerns about the safety of vaccines, combined with the fact that these diseases are now so rare that most people no longer fear them. Parental fear of vaccines is difficult to measure, but (with a few exceptions) it doesn't seem to be a major factor in most poor countries. It would be useful to study the effects of parental fear across countries, but the data simply aren't available. Other explanations include countries' levels of development, how easy it is to reach infants who need to be immunized, the amount that countries spend on health, the number of trained medical personnel in a country who could give immunizations, and the number of children to be immunized. Specific variables that might be used to operationalize each of these explanations are: Level of development National income -- national income per person ('000s of US Dollars) Improved water -- percentage of the population with "improved" water supply (e.g., a well) Improved sanitation -- percentage of the population with "improved" sanitation (e.g., an outhouse) Ease of reach Urbanization -- urban population (percent of the total population) Health spending Health expenditure -- national health expenditure as a percentage of national income Trained personnel Doctors -- number of physicians per 1,000 population Number of children Fertility -- the mean lifetime number of children per woman Other variables could be included, but data for DPT immunization rates plus all seven of these explanatory variables are available in the World Development Indicators for 100 countries representing over 85% of the world's poor countries by population. From a social policy standpoint, we are particularly interested in knowing what can be done to increase the immunization rate. We can't easily make a country richer or more developed, and we can't do much to make children easier to reach or make there be fewer children. On the other hand, we can give countries foreign aid to help them increase their spending on health. We can also seek volunteer doctors to help in administering immunizations. An important policy question is thus: which would be more useful, giving money or finding volunteers? The series of regression models for DPT immunization presented in Figure 9-6 help answer this question. They also illustrate the six reasons for using control variables. The letter for each reason has been attached to its corresponding illustration in the regression table.

Moving from left to right across the models, the inclusion of national income per person as an independent variable (Model 1) is an example of a control variable that makes cases equivalent for comparison (D). The 100 countries included in the analysis differ enormously in their levels of wealth. Controlling for national income helps adjust for those disparities so that we can compare like with like. The inclusion of controls for improved water and improved sanitation (Model 2) is an example of the use of control variable to reduce model error (E). Notice how the R2 score jumps from 15.5% in Model 1 to 46.0% in Model 2. The difference (30.5%) means that the two variables added in Model 2 together explain almost one-third of the total variability in immunization rates. Water and sanitation aren't really direct causes of immunization rates -- you don't need a toilet to conduct an immunization -- but they are general attributes of countries that are more developed. The inclusion of urbanization (Model 3) controls for a potentially competing explanation (C). Despite being significantly correlated with DPT immunization, the coefficient for urbanization is not significant in the regression model after controlling for national income, water, and sanitation. That's not a problem. Urbanization is not being included because of its significance. It's being included because it could potentially compete with our two variables of interest, health expenditure and doctors. The coefficients of heath expenditures and the number doctors are compared in Model 4 and Model 5 (B). Even though the number of doctors has a larger effect, the effect of health expenditures is statistically significant, while the effect of the number of doctors is not. This is a contradictory result, and the reasons for it are not clear. We could try to eliminate one or the other theory by including both health expenditures and doctors in a single model to see if one or the other becomes clearly unimportant when controlling for the other (A). This is done in Model 6. Unfortunately, in Model 6 both coefficients are almost identical, and neither is strongly significant. The odd and ambiguous behavior of the coefficients for health expenditures and doctors may be due to the fact that some other factor is obscuring the true effects of each. A control variable that might bring out these true effects is the fertility rate (F). Countries with high fertility rates have large numbers of children compared to their numbers of adults. This places major burdens on their health systems, since children tend to require much more healthcare than adults. Of course, it places a particular burden on immunization programs, since it is children who receive the DPT vaccine. The same amount of health expenditure or the same number of doctors per person would have much less impact in a country with high fertility than in a country with low fertility. Controlling for fertility (Model 7) increases the coefficient for health expenditure and makes it clearly statistically significant. On the other hand, it dramatically reduces the coefficient for doctors. From Model 7, it seems clear that -- after controlling for other complementary and competing factors -- having higher health expenditures is far more important for promoting immunization than having more doctors. Based on the results reported in Figure 9-6, the best policy would be for rich countries to increase their aid to poor countries rather than to recruit volunteer doctors. If expenditures are increased while holding the number of doctors (and other factors) constant, we would expect immunization rates to rise. If the number of doctors is increased while holding expenditures (and other factors) constant, we would expect no significant change in immunization rates.

9.4. Partialling and the partialling fallacy (optional/advanced) In Model 5 of Figure 9.2, three different operationalizations of social status (education, income, and supervisory status) are used in the same model to explain trust in society. In this model, it turned out that education was significantly related to trust even after controlling for income and supervisory status, while the coefficient for income was only marginally significant and the coefficient for supervisory status was not significant at all. Supervisory position was never very closely related to trust, but in Model 3 income was very highly significantly related to trust in society. In fact, the coefficient for income in Model 3 had a probability of less than .01, indicating that there was less than a 1 in 100 chance that such a strong relationship could have arisen purely at random. Why was the coefficient for income so highly significant in Model 3 but much smaller and only marginally significant in Model 5? The answer, of course, is that education and income are competing controls. Like the coefficient for income, the coefficient for education declined in Model 5, just not as much. Could it have declined more? Since all three variables measure social status, we might have expected none of them to be have significant coefficients. After all, by including three operationalizations of social status in the same model we are effectively measuring the effect of social status while controlling for social status and then controlling again for social status. We might reasonably have expected the three variables to compete with each other more fully in explaining trust in society. We might have expected that, after controlling for social status in one way, other measures of social status would have had no additional impact on trust in society. This didn't happen in Figure 9-2, but it does happen all the time in regression modeling. When two or more operationalizations of the same concept are included in a regression model and they compete to the point where their coefficients end up being non-significant, they are said to "partial" each other. Partialling is a specific form of competition between variables in which the two (or more) variables are alternative operationalizations of the same concept. An example of partialling is depicted in Figure 9-7. Figure 9-7 reports the results of a series of regression models of county murder rates on two operationalizations of county income for 37 large US counties (populations between 500,000 and 1,000,000 people). County murder rates (per 100,000 population) come from the FBI Uniform Crime Reports database. County income is operationalized in two ways. The county poverty rate is the percent of the population in each county that lives on an income of less than the federal poverty line. County median income is the income of the average person in each county. County poverty rates and median incomes come from the US Census Bureau. County poverty rates and county median incomes are correlated r = -0.780. As incomes go up, poverty rates go down.

As would be expected, counties that have higher poverty rates also have higher murder rates (Model 1). Every 1% increase in the poverty rate is associated with a 0.082 person increase in the number of people murdered per 100,000 population. That's not a lot, but it is statistically significant (probability = 0.021, which is less than 5%). Also in line with expectations, counties that have higher median incomes have lower murder rates (Model 2). Every $1000 increase in median income is associated with a 0.031 person decline in the number of people murdered per 100,000 population. Again, the relationship is small but (just) statistically significant (probability - 0.050, or 5%). In Model 3, however, neither poverty nor income is significantly related to the murder rate. Both variables have non-significant coefficients. A researcher who only looked at Model 3 without running models like Model 1 and Model 2 that examined the effect of each variable individually might conclude that neither poverty nor income was significantly related to murder rates. This error is called the "partialling fallacy." The partialling fallacy is a false conclusion that independent variables are not related to the dependent variable when, in fact, they are. The partialling fallacy label applies only in those situations where the variables partialling each other are meant to operationalize the same concept. There are at least three ways around the partialling fallacy. The simplest is to pick just one operationalization of the concept and ignore any others. A better approach is to combine the multiple operationalizations of the concept into a single variable. At the most sophisticated level, multiple operationalizations of a concept can be used together in a model and their joint power to explain the dependent variable studied through their collective impact on the model's R2 score. Notice how the R2 score in Model 3 is slightly higher than that from Model 1 (0.146 versus 0.144). This indicates that poverty and income together explain slightly more of the cross-city variation in murder rates than does poverty alone. The joint analysis of R2 scores has the advantage that it allows the researcher to use all of the available data in all its complexity. On the other hand, complexity is also its main drawback. Sometimes joint analysis adds value, but most times it makes more sense just to keep things simple. Model 1 explains nearly as much of the variability in murder rates as Model 3, without the distraction of managing multiple variables. It would be a reasonable compromise to study city murder rates based on city poverty levels, without worrying about median income.

9.5. Case study: The gender gap in wages in the United States In all countries that have ever been studied, women receive substantially lower wages than men. This doesn't necessarily mean that employers discriminate against women, but the balance of the evidence is that they do. Nonetheless, not all of the age gap is due to discrimination. Two competing explanations of the gender gap are that women accept jobs that pay lower wages in order to have greater flexibility in their family lives and that women earn lower wages because they work fewer hours. There are also other potential competing explanations that will be examined in Chapter 10. Control variables can be used to help us evaluate the validity of these competing explanations. The raw gender gap was illustrated in Figure 4-6 and a primitive regression model of the gender gap was presented in Figure 7-8, but a much more detailed series of explanatory models of the relationship between gender and wages is presented in Figure 9-8. Explanatory models are used instead of predictive models because the goal of the analysis is to understand the gender gap in general, not to predict any particular woman's wages. As in previous chapters, the analyses are restricted to employed twentysomething Americans who identify themselves as being either black or white. Data from Wave 1 of the 2008 Survey of Income and Program Participation (SIPP) have been used. In Figure 9-8 individual wages are regressed on 8 independent variables (including gender) in a series of four regression models.

Model 1 is a base model that includes four background variables: the respondent's age, race, Hispanic status, and years of education. As expected, people have higher incomes when they are older, white versus black, non-Hispanic, and more educated. In Model 2, the coefficient of -7230 indicates that, on average, twentysomething women earn $7,230 less per year than twentysomething men, even after controlling for age, race, Hispanic status, and years of education. Model 3 adds two family variables, marriage and children. Married people earn more than single people and people with children earn less than people without children. These two variables remove some error from the model, but they have very little effect on the gender gap. The possibility that women make less than men because of family obligations can safely be discarded as a competing explanation for women's lower wages. The final, saturated model (Model 4) adds two labor market variables: whether or not people work full-time and whether or not they are attending school (which might mean that they're not working to full potential). Controlling for these competing explanations does reduce the gender gap, but only by $803, from $7,149 to $6,346. These competing explanations both have highly significant coefficients and seem to be important determinants of wages, but they do not explain the majority of the wage differences between women and men. Though the gender gap may not be due to discrimination, we can conclude from the models presented in Figure 9-8 that it probably isn't caused by family factors or labor market factors. Incidentally, it is impossible for any of the variables in Figure 9-8 to be confounded with gender because gender is determined randomly at the time of conception, but there may be other confounded effects. For example, it is possible that older people are more educated (since the youngest people in the sample would not have finished their educations by the time of the study) and earn higher wages, so education is likely to be confounded with age. This might be a problem if the purpose of the analysis was to understand the relationship between education and income, but age and education are used here only with the intent of making cases equivalent for comparison. Similarly, marriage and children may be confounded, but again this is not an issue from the standpoint of the gender gap. The models presented in Figure 9-8 are reasonably parsimonious. Very few variables are included, and all of them have statistically significant effects. A fuller model of twentysomething wages might control for many more variables and still not be considered overly complex. For example, an important alternative explanation of the gender gap in wages is that it might be due to women's choices of what industry to work in. This will be investigated further in Chapter 10.

Chapter 9 Key Terms

Base models are initial models that include all of the background independent variables in an analysis that are not of particular theoretical interest for a regression analysis.
Confounding variables are variables that might affect both the dependent variable and an independent variable of interest.
Explanatory models are regression models that are primarily intended to be used for evaluating different theories for explaining the differences between cases in their values of the dependent variable.
Parsimony is the virtue of using simple models that are easy to understand and interpret.
Predictive models are regression models that are primarily intended to be used for making predictions about dependent variables as outcomes.
Saturated models are final models that include all of the variables used in a series of models in an analysis.

Multiple Categorical Predictors: ANOVA Models

In the Twentieth Century Germany invaded its neighbors in two tragically destructive wars. World War I (1914-1919) and even more so World War II (1939-1945) left Europe in ruins. In the seven years of World War II in Europe, roughly 18 million soldiers and 25 million civilians lost their lives, including 6 million Jews systematically killed in the Holocaust. These deaths amount to around 7% of the total population of Europe at the time, or about 1 out of every 13 people. It is difficult for us today to comprehend the scale of the losses. After the slaughter of World War II, European leaders were adamant that Europe should never go to war again. In 1951 six western European countries signed a treaty that set up the European Coal and Steel Community. In the sixty years since then, this limited international partnership has evolved into a European Union (EU) of 27 countries with a combined population of over 500 million people and an economy larger than that of the United States. Today's EU is dedicated to supporting peace, development, democracy, and human rights across Europe. It does this through economic cooperation and collective decision-making in which the approval of all 27 countries is required for major decisions. Considering its 60-year track record of preventing war and promoting prosperity across Europe, we might expect European citizens to have a high level of confidence in the EU. In fact, they do not. Over the years 2005-2008 the World Values Survey (WVS) was conducted in eleven EU countries. Two additional countries (Bulgaria and Rumania) participated in the WVS in 2006 and joined the EU one year later in 2007. In all thirteen countries, survey respondents were asked how much confidence they had in the European Union. Placed on a scale from 0 to 3, the available answers were: 0 -- None at all 1 -- Not very much 2 -- Quite a lot 3 -- A great deal The overall mean answer across the thirteen countries was 1.355, much closer to "not very much" than to "quite a lot." Excluding the two countries that had not yet joined by the time of their surveys, the mean was 1.31. In the United Kingdom, which has been an EU member since 1973, the mean level of confidence in the EU was just 1.03. In most countries, people expressed more confidence in "television" than in the EU.

On the other hand, all countries are not alike. People in some countries (like Italy and Spain) did express reasonably high levels of confidence in the EU. The observed mean level of confidence in the EU in the United Kingdom was 1.03 with a standard error of 0.027, so the true mean in the UK is probably somewhere between 0.98 and 1.08 (the observed mean plus or minus two standard errors). Similarly, the true mean for Italy is probably somewhere between 1.68 and 1.76. The true mean for Italy is almost certainly higher than the true mean for the United Kingdom. In Chapter 6 we learned how to use t statistics to evaluate the statistical significance of mean differences between groups, and in fact the difference between the United Kingdom and Italy is highly significant (t = 19.653 with 1850 degrees of freedom, giving a probability of .000 that the difference could have arisen by chance). How big are the cross-national differences in confidence in the European Union overall? One way to answer this is to ask whether or not the cross-national differences are statistically significant. We can use simple regression models to evaluate the significances of the mean differences between any two groups, but with 13 countries there are 78 distinct pairs of countries that could be compared. Obviously, we wouldn't want to compare all of them. We could instead compare each of the countries to the overall European mean. This is a more reasonable strategy, but it still requires thirteen separate comparisons that then have to be combined somehow. A completely different strategy would be to pick one country (like the United Kingdom) and compare all the other countries to it. This approach wouldn't provide significance levels for every possible comparison of countries, but it would be a start. If the twelve other countries were compared to the United Kingdom within a single multiple linear regression model, the R2 score would give some indication of how much of the total individual variability among respondents in confidence in the EU could be accounted for by differences between countries. This approach would have the added benefit that we already know how to use other variables multiple linear regression. Between-country differences could be included in larger regression models to explain dependent variables using both group memberships and ordinary independent variables.

This chapter introduces a new type of regression model design, the ANOVA model. First, mean models can be used to study how means differ across groups of cases (Section 10.1). The main limitation of the mean model is that it can only be used to examine each group individually, when what we really want to do is to consider all group differences together at the same time. Second, regression models can be used to determine the statistical significance of the differences between groups (Section 10.2). Importantly, they also tell us the total percentage of the variability in the dependent variable that can be traced to group differences. Third, ANOVA models can be embedded into larger regression models to create models that combine aspects of each (Section 10.3). These mixed models are interpreted no differently from ordinary regression models. An optional section (Section 10.4) develops a new statistic, the F statistic, that can be used to evaluate the overall statistical significance of an ANOVA model or any other regression model.. Finally, this chapter ends with an applied case study of racial differences in education levels in the United States (Section 10.5). This case study illustrates how group differences in he values of a dependent variable can be explained using mixed models. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should understand how regression can used to study between-group differences in the values of an independent variable.

10.1. Comparing group differences using mean models The natural way to think of group differences in the values of a variable is to think of each group as having a mean of its own. For example, in Figure 10-1 each of the thirteen countries has its own mean level of confidence in the EU. The 885 Bulgarians have a mean of 1.63, the 1,049 Cypriots have a mean 1.41, and so on down the list. This is the way people usually look at group means, and it is very intuitive. The problem with this approach is that it isn't necessarily an accurate reflection of reality. In reality, individual Europeans report more or less confidence in the EU for a variety of reasons. One of those reasons is the country in which a person lives. Another might be the person's age. More potential reasons include the person's gender, the person's level of education, the person's income, and whether or not the person has ever received funding or other assistance directly from the EU. Confidence in the EU as reported on the WVS can even be attributed in part to whether or not it was a sunny day when the question was asked: people are more likely to rate things highly on a sunny day than on a cloudy day. For all these reasons, a more appropriate way to think about group means is to think of them as group differences in the values of a single variable. The simplest way to do this is using a mean model (Chapter 4). Applying this approach to the European data, there is an overall mean level of confidence in the EU for all Europeans. People's actually reported levels of confidence at any particular time differ from this true mean for a wide variety of reasons. One of those reasons is their country of residence. The mean level of confidence in the EU for each country depends on the specific history and circumstances of that country. Mean models can be used to evaluate whether or not the true means for each country are significantly different from the overall mean level of confidence in the EU for all Europeans. In Chapter 6 we learned how to use the t statistic to evaluate the probability that a true mean might be zero. We can just as easily evaluate the probability that a true mean might be any number. In this situation, we want to know the probability that the true mean level of confidence in the EU in each country might be equal to the overall European mean. The observed mean across all European WVS respondents (14,154 individuals divided into 13 countries) was 1.355. Using the means for each country and their standard errors, t statistics can be calculated to evaluate how far each one is from the European mean. These t statistics and their associated probability levels are reported in Figure 10-2.

Based on the results reported in Figure 10-2, mean levels of confidence in Poland (mean = 1.39) and Cyprus (mean = 1.41) are not significantly different from the overall European mean, while the means for all other countries are highly significantly different from the overall European mean. Since some countries are significantly above the European mean and other countries are significantly below the European mean, we can conclude that overall there are important cross-national differences between European countries in confidence in the EU. In this example, nearly all of the t statistics are so highly significant that it is easy to see that the differences between countries matter. In other situations, things might not be so clear. For example, we might want to know whether or not there are regional differences in countries' success in immunizing young children against disease. An international database of rates of diptheria-pertussis-tetanus (DPT) immunization was described in Chapter 9. The database includes data for 100 poor countries organized into six regions. The distribution of the 100 countries in the database by official World Bank region is: EAP -- East Asia & Pacific (14 countries) ECA -- Eastern Europe & Central Asia (19 countries) LAC -- Latin America & Caribbean (9 countries) MNA -- Middle East & North Africa (8 countries) SAS -- South Asia (8 countries) SSA -- Sub-Saharan Africa (42 countries) The DPT vaccine is given to infants aged 12-23 months old. The mean immunization rate for infants these ages across all 100 countries is 81.2%. In five of the six World Bank regions the immunization rate is higher than 81.2%, but in one region (Sub-Saharan Africa) it is lower. The regional mean DPT immunization rates are plotted in Figure 10-3. The 100-country mean has also been placed on the chart as a reference line.

The mean model approach that was can be used to study cross-regional differences in DPT immunization rates. In the DPT example, the cases are countries and the countries are grouped into regions. In Figure 10-4, regional deviations from the overall 100-country mean of 81.23% are evaluated using t statistics. Of the six World Bank regions, two (ECA and LAC) have DPT immunization rates that are significantly higher than the 100-country mean, one (SSA) has a DPT immunization rate that is significantly lower than the 100-country mean, and three (EAP, MNA, and SAS) have DPT immunization rates that are not significantly different from the 100-country mean.

With two higher, one lower, and three the same, can we conclude that there are meaningful regional differences in DPT immunization rates? It's not so clear as in the EU example. The answer is probably yes (three of the six regions do show significant differences), but we don't have any firm guidelines to back this up.

10.2. ANOVA as a regression model Mean models can be useful for answering simple questions about the levels of variables, but most social scientists rarely use them. Social scientists usually want to study multiple aspects of how independent variables affect a dependent variable, and this can only be done in the context of regression modeling. In a regression model (or series of regression models), the total observed variability in a dependent variable can be divided up many different ways. The only real limitation of regression modeling is that all of the variables (both dependent and independent) have to be represented by numbers. You can't use a variable like the respondent's country of residence in a regression model. Most of the time when we talk about variables, statistics, and regression models we think of numbers. We have some data about a person (like age or years of education) that usually start at zero and run up from there. Numerical variables are variables that take numerical values that represent meaningful orderings of the cases from lower numbers to highest numbers. Numerical variables don't have to start at zero. For example, they could also be negative, like the gender gaps in science in different countries (Figure 7-1). It is possible for a variable to use numbers as values but still not be a numerical variable, but this is rare. For example, region codes for DVDs divide the world into six regions (1-6), but the numbers don't have any real meaning as numbers. There's no sense in which Region 2 (Europe) is "more regional" than Region 1 (North America). On the other hand, variables like WVS respondents' countries of residence (Figure 10-1) and the World Bank region in which a country is located (Figure 10-3) aren't attached to numbers at all. Instead, the values of these variables are names that describe groups of cases. Variables like World Bank region that describe groups of cases with names instead of numbers are called categorical variables. Categorical variables are variables that divide cases into two or more groups. Categorical variables include both variables with multiple groups (like World Bank region and WVS country) and variables with just two groups (like "gender" coded as being either male or female). Since categorical are not numeric, they can't be added, subtracted, multiplied, or divided. They also can't be used in regression models. When we've wanted to use categorical variables like gender in regression models, we've had to code them as 0/1 variables where one gender took the value "0" and the other gender was coded as "1." Even though the variable "gender" (male/female) is categorical, the variable "female" (0=no, 1=yes) is numerical. It represents how female the respondent is: 0 (not at all) or 1 (completely). Because "female" is numerical, it can be used in regression models. For example, in Model 2 of Figure 9-8 the coefficient for "female" was -7230, indicating that (after controlling for other factors) being female changed a person's expected wage by 1 x -7230 = -$7,230 compared to people who weren't female. Categorical variables with more than two groups are more complex. A special kind of regression model design exists to accommodate these variables. These models are called "analysis of variance" models. Analysis of variance (ANOVA) is a type of regression model that focuses on the proportion of the total variability in a dependent variable that is explained by a categorical variable. Since all regression models involve the analysis of variance, it's a little strange to use the name "analysis of variance" to refer to just this one type of regression model. Unfortunately, the name has been widely used in the social sciences for at least half a century, so it's too late to change it to something better. Partly as a response to this awkwardness, most social scientists today use the acronym "ANOVA" when referring to regression models that use categorical independent variables instead of spelling out the full name. Before categorical variables can be used in ANOVA models they have to be recoded into numerical variables. These new numerical variables are called ANOVA variables. ANOVA variables are the numerical variables in a regression model that together describe the effects of categorical group memberships. When a categorical variable only has two groups (like gender), it can be recoded into a single ANOVA variable (like female = 0 for men and 1 for women). This single numerical variable can then be used as an independent variable in regression models. When a categorical variable has three groups, two new variables are needed. For example, consider the variable "party affiliation" which in most US election surveys must take one of three values (Democratic, Republican, Independent). This can be recoded into the two ANOVA variables: Democratic -- coded 1 for Democrats and 0 for all others Republican -- coded 1 for Republicans and 0 for all others These two numerical variables can then be used as independent variables in a regression model. Why isn't there a third variable for Independents? Because if a person has the value "0" for the variable "Democratic" and the value "0" for the variable "Republican," that person must be an Independent. No extra variable is needed. More than that: if you tried to use a third variable for Independents in a regression model, the program wouldn't allow it. A categorical variable with two groups (gender) uses one ANOVA variable, a categorical variable with three groups (party) uses two ANOVA variables, a categorical variable with four groups uses three ANOVA variables, etc. The number of ANOVA variables is always one less than the number of groups in the original categorical variable. So for example the categorical variable describing what World Bank region a country belong to has six groups: EAP, ECA, LAC, MNA, SAS, and SSA. Before this categorical variable can be used in regression models, it has to be recoded into five ANOVA variables. One group is set aside and not made into a new variable. This group is known as the reference group. Reference groups are the groups that are set aside in ANOVA variables and not explicitly included as variables in ANOVA models. Setting aside SSA (Sub-Saharan Africa) as the reference group, the five ANOVA variables for World Bank region are: East Asia & Pacific -- coded 1 for EAP countries and 0 for all others Eastern Europe & Central Asia -- coded 1 for ECA countries and 0 for all others Latin America & Caribbean -- coded 1 for LAC countries and 0 for all others Middle East & North Africa -- coded 1 for MNA countries and 0 for all others South Asia -- coded 1 for SAS countries and 0 for all others Any country that is coded "0" on all five of these ANOVA variables must be, by process of elimination, an African country. A regression of DPT immunization rates on these five ANOVA variables is presented in Figure 10-5. The R2 of this model, 0.297, indicates that World Bank region explains 29.7% (almost 30%) of the total variability across countries in DPT immunization rates.

The coefficients in Model 1 of Figure 10-5 can be read just like those of any other regression model. When all five independent variables equal "0," the expected value of the DPT immunization rate is 71.7% (the constant). What does this mean? It means that 71.7% is the conditional mean rate of DPT immunization in Sub-Saharan Africa. In a straightforward ANOVA model like this, the constant gives the conditional mean value of the dependent variable for the reference group. This is no different from a simple regression model like that reported in Figure 4-6, where the constant represented the mean income for women (since for women, the value of the variable "Male" was 0). In Figure 10-5, Sub-Saharan African countries have the value 0 on all five ANOVA variables. As a result, their expected DPT immunization rates are: 71.7 + 11.3 x 0 + 22.5 x 0 + 15.7 x 0 + 18.1 x 0 + 9.6 x 0 = 71.7%. You can confirm this by looking up Africa's mean rate of DPT immunization in Figure 10-4. The coefficients for the five ANOVA variables represent the difference in mean DPT immunization rates between Sub-Saharan Africa and each of the regions. For example, the expected DPT immunization rate for countries in the World Bank region of Latin America & Caribbean is: 71.7 + 11.3 x 0 + 22.5 x 0 + 15.7 x 1 + 18.1 x 0 + 9.6 x 0 = 87.4%. Again, you can confirm this by looking it up in Figure 10-4. Since the actual regression coefficients in an ANOVA model represent differences from the reference group, different reference groups will yield different results. In Figure 10-5, all the coefficients are positive because every World Bank region has a higher mean level of DPT immunization than Sub-Saharan Africa. By contrast, every World Bank region has a lower mean level of DPT immunization than Eastern Europe & Central Asia. In an identical ANOVA using Eastern Europe and Central Asia as the reference group, all the coefficients would be negative. This is illustrated in Figure 10-6. In Figure 10-6, the R2 is the same as in Figure 10-5, but all the coefficients (including the constant) have changed.

The R2 is still 0.297, since World Bank region explains 29.7% of the cross-national variability in DPT immunization rates no matter what region is used as the reference group. The constant now represents the mean level of DPT immunization in Eastern Europe & Central Asia (the reference group). The coefficients for the regions now represent the differences between those regions' mean levels of DPT immunization and the level in Eastern Europe & Central Asia. Note that although all of the coefficients have changed, all of the expected values generated by the model remain the same. For example, the expected DPT immunization rate for countries in the World Bank region of Latin American & Caribbean is still: 94.3 - 11.3 x 0 - 6.8 x 1 - 4.4 x 0 - 12.9 x 0 - 22.5 x 0 = 87.5%. The slight difference from the earlier result (87.4% versus 87.5%) is due to rounding. No matter what group is chosen as the reference group in an ANOVA analysis, the R2 and the conditional means for each category (calculated from their expected values) remain the same. The only real difference between Figure 10-5 and Figure 10-6 is in the statistical significance of the coefficients. In Figure 10-5, all of the groups are compared to Sub-Saharan Africa, while in Figure 10-6 all of the groups are compared to Eastern Europe & Central Asia. The reported significance levels relate to how different the mean for each group is from the mean of the reference group, and different reference groups will produce different significance levels. As a result, in ANOVA models the specific statistical significance of each of the ANOVA variable coefficients is not usually very important. The ANOVA analyses reported in Figure 10-5 and Figure 10-6 are preferable to the six mean models reported in Figure 10-4 for several reasons. First, the ANOVA models tell us the total proportion of the cross-national variability in immunization rates that is due to differences between World Bank regions (almost 30%). Second, it tells us this using a single model (instead of six models). Third, it integrates the analysis of categorical independent variables into a regression modeling framework. This final point is by far the most important, because it allows us to apply all the tools of regression modeling to the study of the effects of categorical independent variables.

10.3. Mixed models ANOVA models are just regression models with a very particular setup of independent variables. Once appropriate ANOVA variables have been created to represent a categorical variable, they can be used in other regression models as well. For example, Figure 9-6 presented a series of seven regression models that used seven different variables to explain cross-national differences in DPT immunization rates. In Figure 10-7, these variables are combined with World Bank region into a single analysis that includes models that mix ANOVA variables with numerical variables. Mixed models are regression models that include both ANOVA components and ordinary independent variables. Like the coefficients of ANOVA models, the coefficients of mixed models are just ordinary regression coefficients and are interpreted the same way as any other regression coefficients.

Model 1 in Figure 10-7 is a base model that includes general development variables that are not directly related to immunization. Model 2 adds the five ANOVA variables for region. After controlling for level of development, the regional differences are much smaller than they were in Figure 10-6 (which also used Eastern Europe & Central Asia as the reference group). This indicates that most of the differences between region are due to regional differences in level of development. In fact, the R2 of Model 1 is 0.467 while the R2 of Model 2 is 0.476, for an improvement of just 0.009. This means that after controlling for level of development (Model 1), the additional explanatory power due to regional differences (Model 2) is just 0.9%. Health and demographic variables add much more explanatory power, bringing the final proportion of the cross-national variability in immunization rates explained by the models to 54.3% in Model 4. In the mixed model presented in Figure 10-7 the ANOVA variables add very little explanatory power and are not statistically significant (at least when Eastern Europe & Central Asia is used as the reference group). In other mixed models the ANOVA variables can have much greater impact. Figure 10-8 builds on Figure 9-8, using mixed models to improve our understanding of the gender gap in wages among American twentysomethings. In Figure 9-8, race was operationalized using a simple distinction between whites and non-whites. In Figure 10-8, race is operationalized as a four-group ANOVA variable, using whites as the reference group. Figure 10-8 also includes another ANOVA variable in Model 5: the industry in which a person works.

Industry in Figure 10-8 is operationalized as a categorical variable taking four possible values: AMM -- Agriculture, mining, and manufacturing Trade -- Wholesale and retail trade Services -- Education, healthcare, financial, and other services Government -- Federal, state, and local government, plus non-profit organizations The highest-paid group, AMM, has been used as the reference group. The coefficients reported in Model 5 indicate that (after controlling for all other variables) people working in trade and services make significantly less than people working in AMM, while people working in government make slightly (not significantly) less. Controlling for industry has very little effect on the R2 of the models (R2 improves from 0.210 to 0.214, or 0.4%), but it has a big effect on the gender gap. In Model 4, the gender gap is $5,501. This means that even after controlling for age, race, ethnicity, education, marriage, children, employment status, and educational enrollment, twentysomething American women are still found to make $5,501 less than twentysomething American men. Even after all those controls have been taken into account, controlling for the industry in which a person is employed reduces the gender gap by a further $791 a year, to $4,710. This is a pretty substantial drop, considering that industry has been only very broadly accounted for (for example, education, health, and finance have all been lumped together in "services"). Better controlling for industry and occupation would likely reduce the gender gap further. On the other hand, the gender gap is still very substantial, amounting to over $4000 out of a typical wage of $20,000 or so a year. Ever after controlling for many competing explanations, the gender gap in wages for American twentysomethings is at least 20%, and probably larger.

10.4. ANOVA and the F statistic (optional/advanced) Despite the fact that ANOVA is (mathematically) a regression model, most textbooks present it before teaching regression and do not draw a connection between the two. Instead, ANOVA is taught only as a tool for evaluating group differences. In this approach, the key question asked in ANOVA analysis becomes: are there significant differences between groups in the values of the dependent variable? This question is answered by comparing the differences in the values of the dependent variable between groups to the remaining differences in the values of the dependent variable within each group. If the between-group differences are large relative to the within-group differences, the ANOVA model explains a significant portion of the overall variability in the dependent variable. If the between-group differences are very small, the ANOVA model is not significant. This traditional approach is illustrated in Figure 10-9. Figure 10-9 uses the same DPT immunization data as Figure 10-3, but unlike Figure 10-3 it shows the immunization rate for every one of the 100 countries in the database of poor countries. A few sample countries have been labeled on the graph. Each country deviates from the overall mean of 81.2% immunization by a different amount and for different reasons. For example, the DPT immunization rate in Guinea is just 51.0%, far below the overall mean of 81.2%. Part of the reason DPT immunization in Guinea is so low is that it's in Africa, and part of the reason is model error that is specific to Guinea. The same division can be made for every country: part of each country's deviation from the overall mean immunization rate is due to its region, while part of its deviation is due to model error.

In the traditional ANOVA model, the deviations of the regional means from the overall mean are all squared and summed up into a sum of squared deviations. The remaining deviations of the countries from their regional means are also squared and summed up. Then the two sums are compared to determine whether or not the deviations due to region make up a statistically significant proportion of the total squared deviations. This process is summarized in Figure 10-10 for the DPT data. The sum of squared deviations for the regions is 8000.93, while the sum of squared error deviations is 18944.78. Each sum of squared deviations is then divided by its degrees of freedom. Since the six regions can be fully described using five ANOVA variables, region overall (as a categorical variable) only has five degrees of freedom. As with the t statistic (Chapter 6), estimating the mean also takes up one degree of freedom. Since there are 100 cases, this means that there are 100 - 5 - 1 = 94 degrees of freedom left over for model error.

The ratio of the mean squared deviation per degree of freedom attributable to group effects to that attributable to error is called the "F" statistic (named in honor of statistician Ronal Fisher). The F statistic has two different degrees of freedom, one for its numerator and one for its denominator. In Figure 10-10, the F statistic for the explanatory power of region is 7.94 with 5 and 94 degrees of freedom. Using a reference book or statistical software program to check its significance, this F statistic is associated with a probability of 0.000. World Bank region significantly predicts DPT immunization rates. The F statistic is usually taught with reference to ANOVA, but it actually applies to all regression models. Regression output from statistical software programs almost always includes the F statistic. It's not often used because it is almost always statistically significant. It's a rare regression (or ANOVA) model that doesn't explain a significant proportion of the overall variability in the dependent variable. The F statistic has some useful advanced applications in comparing the explanatory power of nested regression models (sets of models in which one model includes all of the variables used in another model, plus some additional variables), but it is not very useful for describing the results of ANOVA models. The R2 statistic is usually far more useful for diagnosing whether or not group differences are substantively meaningful.

10.5. Case study: Racial differences in education in the United States Americans of difference races have always faced different educational opportunities. Before the 1960s, many schools and universities were entirely closed to black students, and some schools and universities also discriminated against students of Asian and other racial backgrounds. In addition to outright discrimination by schools, people of different races also faced a range of educational barriers based on income, location, awareness of opportunities, and many other factors. Figure 10-11 reports the racial differences in education among American adults age 30 and over among participants in the 2008 Survey of Income and Program Participation (SIPP), Wave 2. The focus is on people aged 30 and over because most people have finished their education by age 30.

The data reported in Figure 10-11 show clear differences in educational levels between races. Asian Americans having the highest levels of education, while people of African American and "Other" race (mainly Native Americans) the lowest. An ANOVA model confirms that all three of these races have mean levels of education that are significantly different from Whites.. The categorical variable "race" is operationalized into three ANOVA variables in Model 1 of Figure 10-12. The White group is used as the reference group. The education levels of Asians, blacks, and others are all highly significantly different from those of whites, with Asians having more education and Blacks and Others less. On the other hand, despite the fact that these differences are very highly statistically significant, they explain less than 1% of the total individual variability in education. Most of the individual variability in levels of education are apparently unrelated to race. It is possible that at least some of the differences in levels of education between races in the United States is due to differences in the age and gender composition of the American population by race: age and gender may be confounding variables in Model 1. This proposition can be examined using a mixed model that controls for the numerical variable age alongside the categorical variable race. A base model using just age and gender to predict education is presented in Model 2 and a mixed model including race as well in Model 3. The coefficients of the ANOVA variables in Model 3 indicate that the gaps between Whites and Blacks and Whites and Others are actually larger after controlling for age and gender, not smaller. Controlling for age and gender, Blacks receive on average 0.581 fewer years of education than Whites, while Others receive 0.714 fewer years of education.

Clearly, racial differences in education exist in the United States. That is not very surprising, given what we know about the long history of racial discrimination and disadvantage in US society. It might be more interesting to know how the racial gap in education has changed over time. The older Americans in the SIPP sample grew up in a racially segregated America that often didn't allow non-Whites to attend universities, while the younger Americans in the SIPP sample grew up in a society that was officially race-free or even promoted attendance for racial minorities. Hopefully, this means that the racial gap is declining over time. Is the racial gap in education smaller for younger Americans who came of age in the 1980s and 1990s than it is for older Americans who came of age in the 1950s and 1960s? Answering that question requires a new type of model, the interaction model, that is the focus of Chapter 11.

Chapter 10 Key Terms

Analysis of variance (ANOVA) is a type of regression model that focuses on the proportion of the total variability in a dependent variable that is explained by a categorical variable.
ANOVA variables are the numerical variables in a regression model that together describe the effects of categorical group memberships.
Categorical variables are variables that divide cases into two or more groups.
Mixed models are regression models that include both ANOVA components and ordinary independent variables.
Numerical variables are variables that take numerical values that represent meaningful orderings of the cases from lower numbers to highest numbers.
Reference groups are the groups that are set aside in ANOVA variables and not explicitly included as variables in ANOVA models.

Interaction Models

It is often said that education is the key to a better life. Education makes people more intelligent and better-informed. Education opens up people's minds to new ideas, new experiences, and new opportunities. Education even leads to better health. Education has all these effects because education changes people's very identities. Because you pursued higher education, you are a different person than you would have been. You may not like to admit that attendance at a college or university is changing you, but for better or worse it is. It is impossible to spend several years of your life studying and socializing in an academic setting without being affected in any way. For most people, education leads to a fuller, happier, longer life. Education is also closely associated with income. The education people complete early in life is highly correlated with the wages they earn years later. This is true all over the world, in rich countries and poor countries alike. There are many reasons why more educated people earn higher wages than less educated people. First of all, people who have rich and highly educated parents and tend to receive more education themselves, so more-educated people often start out with more advantages then less-educated people. More importantly, educational credentials are required for admission to many careers, ranging from massage therapists to cancer doctors and everything in between. Education also gives people knowledge and social contacts that help them in their careers. Whatever the reasons, the fact is clear: more highly educated people earn higher wages than less highly educated people. We saw this in Figure 10-8. Though Figure 10-8 focused mainly on the gender gap in wages, it also showed that every extra year of education results in over $3000 more in expected wages for twentysomething Americans. This figure was shown to be robust across all five models estimated. The coefficients for education in Figure 10-8 ranged from a low of 3065 in Model 1 to a high of 3262 in Model 2, with the coefficients for the other models falling somewhere in between these two figures. A coefficient over 3000 means that a four-year college degree is worth more than $12,000 a year in extra wages ($3000 per year x 4 years) to a typical twentysomething American. Unfortunately, as we learned in Figure 10-10 and Figure 10-11, education in America depends strongly on race. This is true in other countries as well, but more detailed data on the subject are available for the United States than for any other country. Among Americans aged 30 and over, Asians are the most educated, followed by Whites, then Blacks, then Others. Model 1 of Figure 10-11 showed that Asians complete on average 0.632 more years of schooling than Whites, while Blacks complete 0.556 fewer years of schooling than Whites. Racial differences overall explain less than 1% of the differences in education between individuals (R2 = .008), but the effects of race are nonetheless statistically significant and substantively important. Figure 11-1 explores the role played by education in explaining racial differences in wage income for Americans aged 30 and over. Data come from the 2008 Survey of Income and Program Participation (SIPP), Wave 2. Model 1 of Figure 11-1 is a straightforward ANOVA model in which wages are regressed on race. The categorical variable "race" has been operationalized using three ANOVA variables: Asian, Black, and Other. The reference group is White. The coefficients for Asian, Black, and Other represent the mean wage differences between people of these races and Whites. The difference is especially large for Blacks. On average, Black Americans aged 30 and over earn $8,746 less than White Americans. Asian Americans earn (on average) $5,991 more than Whites. Combining these two figures, Asian Americans earn (on average) 5991 + 8746 = $14,737 more than Black Americans.

These differences between races are highly significant, but together they explain only a small proportion (juat half a percent) of the total variability in Americans' wages. This doesn't mean that race is unimportant. Around 80% of the American population identifies itself as White (including White Hispanics, such as most Mexican Americans). Since most of the population is White, most of the variability in people's wages is variability among White people. In other words, it is only possible for race to matter for the 20% of the population that is not White (considering White to be the reference group). Even for those people, other factors (like age, education, occupation, industry, place of residence, and employment) may matter more. So it's not surprising that race on its own explains only 0.5% of the total variability in people's wages. The large and significant coefficients in Model 1 indicate that race is important. Since we know from Figure 10-11 that levels of education differ significantly across races in the United States, we might hypothesize that the racial differences in wages observed in Model 1 of Figure 11-1 are due to racial differences in education. After all, if Blacks receive significantly less schooling than Whites, it would not be surprising to find that (on average) they earn lower wages. To investigate this possibility, Model 2 of Figure 11-1 controls for education. Since race is a categorical variable and education is a numerical variable, Model 2 is a mixed model. In Model 2, controlling for education reduces the racial gaps in wage income, but the remaining gaps are still highly significant. Model 2 indicates that Black Americans aged 30 and over and earn (on average) $5,810 less than white Americans of similar education levels. The affect of an additional year of education in Model 2 ($5,269) is almost as large as the wage gap between Blacks and Whites ($5,810). This suggests that one way to address racial differences in wages might be to encourage higher levels of education for Blacks. Right now, Blacks receive on average 0.556 fewer years of schooling than Whites (Model 1 of Figure 10-11). Might raising Black educational levels also raise wages for Blacks? Based on Model 2 of Figure 11-1, the answer seems like it might be yes. On the other hand, it is possible that an additional year of education will raise wages less for Blacks than for Whites. If this happens, it would be very difficult to use education to address the racial gap in wages. Figure 11-2 illustrates the differences between races in the effects of an additional year of education. For Whites, every additional year of education is associated with an increase of $5,393 in wage income. For Asians, the effect is similar, but slightly smaller ($5,298). For Blacks and Others, the economic impact of each additional year of education is much smaller. Black Americans earn on average an additional $4,394 in wage income for each additional year of education, while others earn an additional $4,422 for each year of education.

The results reported in Figure 11-2 are troubling. To begin with, Blacks and Others already have lower education levels on average than Whites and Asians. Then even when Blacks and Others do pursue higher education, they get less benefit from it (in terms of wages) than Whites or Asians. For example, the results reported in Figure 11-2 suggest that a four-year college degree raises White incomes by 5393 x 4 = $21,572 for adults aged 30 and over, while the same college degree raises Black incomes by just 4394 x 4 = $17,576. This is a big difference. On the other hand, we can't tell for sure that the racial differences reported in Figure 11-2 are statistically significant. All the coefficients are significantly different from zero, but that doesn't mean that they are significantly different from each other. It might be that the differences between the coefficients for education in the White model (5393) and the Black mode (4394) are just due to random error in the SIPP data. It seems pretty clear that they are different, but ideally we'd like to know for certain that the difference is statistically significant.

This chapter explains how regression models can be designed to evaluate the significance of group differences in the sizes of regression coefficients. First, special variables called "interaction variables" have to be constructed (Section 11.1). When these are used in regression models they reveal group differences in the slopes associated with independent variables. Second, the inclusion of an interaction variable in a regression model changes the meanings of both the slopes and the intercept for the model (Section 11.2). These changes are most easily understood using graphs to plot the model's regression lines. Third, models with interaction variables can have other control variables just like all other regression models (Section 11.3). In fact, interaction effects are most often found embedded in larger regression models. An optional section (Section 11.4) demonstrates how interaction variables can be calculated using ANOVA variables and applied to many groups at the same time. Finally, this chapter ends with an applied case study of the differences in the economic value of education between the United States and France. (Section 11.5). This case study illustrates how the effects of independent variables can differ significantly across groups of cases. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should understand how to evaluate and interpret between-group differences in regression models.

11.1. Interaction variables Does money set you free? That is to say, does having more money make people feel a greater sense of freedom in life? Not surprisingly, it does. In every country of the world for which data are available, there is a positive correlation between people's sense of personal freedom and their levels of income, though in some countries the relationship is not statistically significant. In the World Values Survey (WVS), personal freedom is measured using the question "How much freedom do you feel?" for which respondents circle a number ranging from 1 "none at all to 10 "a great deal." Mean levels of personal freedom across countries generally run around 7-8 on the scale from 1 to 10, with the poorest people in each country reporting scores that are 1-3 points less than the richest people. Clearly, income matters for people's feelings of freedom, but does it matter the same for all people? In particular, might income matter more for men than for women (or vice versa?). One country where income matters a great deal is Poland. Poland has one of the strongest correlations between income and feelings of freedom anywhere in the world (r = 0.239). Regression models for the impact of income on freedom for men and women in Poland are reported in the first two columns of Figure 11-3. Income is measured by breaking the population up into deciles on a scale from 1 (lowest income) to 10 (highest income). For every one point increase in income, Polish men's freedom ratings rise 0.384 points, while for the same increase in income Polish women's freedom ratings rise just 0.206 points. In Poland, money matters more to men than it does to women.

The male and female regression lines for Poland are plotted in Figure 11-4. The expected values of freedom for women are represented by the solid line while the expected values of freedom for men are represented by the dashed line. At low income levels (left side of the graph) women feel freer than men, while at high income levels men feel freer than women. The two lines cross somewhere between income level 4 and income level 5. For Polish people of middle incomes, men and women report roughly equal levels of personal freedom.

Since the slope for men is 0.384 while the slope for women is just 0.206 points, the difference between the slopes is 0.384 - 0.206 = 0.178. Every additional point of income results in 0.178 less freedom for women than it does for men. Income matters more for men than for women, but is this difference (0.178) statistically significant? In other words, is it possible that the true difference is zero, and that the observed difference (0.178) represents nothing more than random error? After all, if the two lines for men and women were drawn on Figure 11-4 purely at random, it's very unlikely that they would match up exactly. One would almost certainly have a steeper slope than the other. What we want to know is whether or not the observed difference in slopes might have arisen purely at random. To answer this question, it is necessary to set up a regression model in such a way that one of the coefficients represents the difference in slopes between men and women. Then, if this coefficient is significantly different from zero, we can conclude that the difference in the slopes is statistically significant. In such a model, the effects of income would be allowed to interact with a person's gender in such a way as to produce different slopes for income depending on a person's gender. Such models are called interaction models. Interaction models are regression models that allow the slopes of some variables to differ for different categorical groups. Interaction models include (at a minimum) three variables: An independent variable of interest (the variable that is thought to have different slopes for different groups) An ANOVA variable (this can be any 0/1 variable) An interaction variable (equal to the independent variable of interest times the ANOVA variable) The interaction variable is at the heart of the interaction model. Interaction variables are variables created by multiplying an ANOVA variable by an independent variable of interest. In the model for freedom in Poland, the interaction term is computed by multiplying gender (0 for female, 1 for male) by income (scale from 1 to 10). Since gender is zero for all females, the interaction variable is zero for all females (anything times zero is zero). Since gender is one for all males, the interaction variable is the same as income for all males (anything times one is just itself). In concrete terms, the interaction model for freedom in Poland reported in the final column of Figure 11-3 is: Freedom = 5.770 + 0.206 x Income - 0.805 x Gender + 0.178 x Gender x Income For women (gender = 0), this is the same as: Freedom = 5.770 + 0.206 x Income - 0.805 x 0 + 0.178 x 0 x Income Freedom = 5.770 + 0.206 x Income - 0 + 0 Freedom = 5.770 + 0.206 x Income This is the same as the female model reported in Figure 11-3. The interaction model is a little more complicated for men, but not much more. For men (gender = 1), the interaction model is: Freedom = 5.770 + 0.206 x Income - 0.805 x 1 + 0.178 x 1 x Income Freedom = 5.770 + 0.206 x Income - 0.805 + 0.178 x Income Freedom = 5.770 - 0.805 + 0.206 x Income + 0.178 x Income Freedom = 4.965 + 0.384 x Income This is the same as the male model reported in Figure 11-3. If the interaction model just gives the same two models we started with, why run the interaction model at all? One reason is that the interaction model uses all the data (N = 903 cases) all in one model instead of separating the data out into male and female models. Another, much more important reason is that the interaction model tells us the statistical significance of the interaction variable. The coefficient of the interaction variable represents the difference in slopes between the two groups in the model, in this case between men and women. Notice how the coefficient of the interaction variable in the interaction model in Figure 11-3 is 0.178, exactly equal to the difference between the slope for income in the male model and the slope for income in the female model. The interaction model tells us that this coefficient is statistically significant. As a result, we can conclude that the slope of the relationship between income and freedom is significantly higher for men than for women. Income is significantly more important for Polish men than for Polish women in promoting feelings of personal freedom.

11.2. Slopes and intercepts in interaction models In Figure 11-3, it's no coincidence that the results of the male and female models can be calculated from the interaction model. The interaction models is based on the same data and variables as the other models. The only real difference between the interaction models and the two separate models for men and for women is their purpose. The male model is used to evaluate the slope of the relationship between income and freedom for men. The female model is used to evaluate the slope of the relationship between income and freedom for women. The interaction model is used to evaluate the difference between the slope for men and the slope for women. Conveniently, the interaction model can also be used to find out the slope for men and the slope for women, so in the end only one model is necessary. The slope for income reported in the interaction model is the slope for income for the reference group. In the interaction model in Figure 11-3, the reference group is female (gender = 0). The slope for income for women is the main effect reported in the interaction model. Main effects are the coefficients of the independent variable of interest in an interaction model for the reference group. The difference in slopes between women and men in Figure 11-3 is 0.178 (the slope for men is 0.178 points steeper than the slope for women). This is the coefficient of the interaction variable (gender x income) in Figure 11-3. The coefficient of the interaction variable in an interaction model is called an interaction effect. Interaction effects are the coefficients of the interaction variables in an interaction model. When the interaction effect is statistically significant it means that there is a significant difference in slopes between the two groups. The interaction model in Figure 11-3 includes one more variable, gender. The coefficient for gender in the interaction model represents the difference between the intercept of the regression line for men and the regression line for women. This is called an intercept effect. Intercept effects are the coefficients of the ANOVA variables in an interaction model. In the regression of freedom on income for men, the intercept was 4.965, meaning that a man with zero income would be expected to report a personal freedom level of 4.965 on a scale from 1 to 10. In the regression of freedom on income for women, the intercept was 5.770, meaning that a woman with zero income would be expected to report a personal freedom level of 5.770 on a scale from 1 to 10. The intercept effect (-0.805) is the difference between the intercept for men and the intercept for women: 4.965 - 5.770 = -0.805. In interpreting interaction models, we're usually not interested in intercept effects, and they're usually ignored. It's necessary for the ANOVA variable to be included in the model though (like gender in Figure 11-3). Without it, interaction models produce meaningless results. In Poland, we found that income mattered much more to men than to women in determining their feelings of personal freedom. In other countries the situation might be different. Figure 11-5 reports the results of a set of models that are identical to those estimated in Figure 11-3, but this time the models are estimated using data from Australia. For Australian men (male model), every one-point rise in the scale of incomes is associated with a 0.061 point rise in feelings of personal freedom. For Australian women (female model) the associated rise is 0.143 points -- more than twice as much. For both men and women the association between income and freedom is statistically significant, but it is much more significant for women than for men.

The third model reported in Figure 11-5 is the interaction model. This model includes the independent variable of interest (income), a categorical ANOVA variable (gender), and an interaction variable (gender x income). In the interaction model, the main effect of income is 0.143, which is identical to the coefficient for income in the female model. This main effect represents the impact of a one-point increase in income on women's expected feelings of personal freedom. The interaction effect is -0.083. This is the difference between the slope for men and the slope for women in the relationship between income and freedom: 0.061 - 0.143 = -0.083. The interaction effect is statistically significant, indicating that the slope for men is significantly shallower than the slope for women. The intercept effect reported in Figure 11-5 is 0.393, but this is not of any particular theoretical interest. The statistical results reported in Figure 11-5 are graphed in Figure 11-6. The results of interaction models can be difficult to visualize, but plotting them out usually makes them very clear. Figure 11-6 shows that the relationship between income and freedom is weaker for Australian men than it is for Australian women. Both lines rise with income, but the line for women rises faster. Poor women experience less personal freedom than poor men, but rich women experience greater personal freedom than rich men.

Interaction effects are not always significant. In fact, it can be difficult to find significant interactions. For example, in the United States the gender differences in the importance of income are not statistically significant. The results of freedom versus income regressions for the United States are reported in Figure 11-7. The slopes for both men and women are highly significant, but the interaction effect examining the difference in slopes is not.

Figure 11-8 represents the United States results graphically. The two regression lines (women and men) are nearly parallel. The graph seems to show an intercept effect (the line for women is higher than the line for men), but the model results show that this difference is also not significant, though in any case it is not of theoretical interest. In the United States, rich people feel significantly freer than poor people, but there is no evidence of differences between women and men in the importance of income for freedom. For both women and men, higher income makes Americans feel more free in equal measure.

11.3. Interaction effects in mixed models with control variables The results reported in Figure 11-2 showed that every additional year of education raises wages for Whites more than it does for Asians, Blacks, and Others. If education has a different impact on wages for people of different races, might is also have a different impact on wages for people of different genders? In Figure 10-8 it was shown that every extra year of education results in over $3000 more in expected wages for twentysomething Americans. The main results of Figure 10-8 are reprinted as Model 1 in Figure 11-9. Figure 11-9 uses the same 2008 SIPP Wave 2 data to regress wage income on a number of predictors, including gender (coded as 0 for men and 1 for women). Model 1 of Figure 11-9 shows that twentysomething American women earn, on average, $6,591 less than twentysomething American men (after controlling for age, rage, Hispanic status, and education).

Model 2 of Figure 11-9 introduces an interaction variable, Education x Female. In this new model, the main effect of Education is now 3114, indicating that for men (Female = 0) every additional year of education increases the expected value of wages by $3114 The coefficient of the interaction variable (Education x Female) is 312, indicating that for every additional year of education women can expect to receive $312 more than men do. Since men receive $3114 (on average) for every year of education, this means that women receive (on average) 3114 + 312 = $3326 more in wages. The positive interaction effect of 312 means that education actually helps women more than it helps men. This suggests that education could be effective in reducing the gender gap in wages. On the other hand, the interaction effect in Model 2 is not statistically significant. This means that the positive result might have occurred at random. In Model 2 the intercept effect (the coefficient for the variable Female) is -10857. Unlike in Model 1, this coefficient doesn't directly say anything about the differences in wages between women and men. The intercept effect in an interaction model is not very meaningful from the standpoint of interpreting results (though it does have to be included in the model). In order to make conclusions about the overall differences in wages between men and women, you would have to look at the coefficient for Female in Model 1, which doesn't include any interaction effects. Since the interaction between education and gender is not significant, Model 3 in Figure 11-9 examines a different interaction variable: the interaction between gender and age (Age x Female). This interaction is highly significant. As women get older, their incomes lag farther and farther behind men's incomes. The main effect for age in Model 3 (2430) indicates that American men are expected to earn $2430 more every year throughout their twenties. The interaction effect for age (Age x Female) of -786 implies that women's incomes go up by $786 less than men's incomes for every year they get older. In other words, while men's expected wages rise by $2430 a year, women's expected wages rise by 2430 - 786 = $1644 a year. This is a large and statistically significant difference (probability < .001). Aging is incredibly more remunerative for men than it is for women. There's no reason why both interaction variables can't be included in the same model. This is done in Model 4. In Model 4, both interaction effects are significant, but the interaction for age is much more so. In Model 5, additional control variables are included alongside the interaction variables. Even after controlling for marriage, children, full-time employment status, school enrolment status, and industry of employment, the interaction effect for age remains highly significant. On the other hand, the interaction effect for education is reduced to a very small and insignificant figure (less then $100 per year of education). The results reported in Model 5 suggest that additional education will not do much to reduce the gender gap in wages between men and women in America. Instead, the gap tends to widen further and further as men and women age, at least over the course of their twenties. As Figure 11-9 illustrates, interaction effects can be used in mixed models with other numerical and categorical independent variables. Multiple interaction effects can even be estimated within a single model. The interpretations of these models are no different from the interpretation of ordinary regression and interaction models. Any model that includes both numerical and ANOVA variables can include one or more interactions as well.

11.4. Multiple categorical interactions (optional/advanced) If a regression model can include multiple interactions for the same ANOVA variable (education and age by gender in Figure 11-9), it stands to reason that a regression model can include the same interaction for multiple ANOVA variables. In Figure 11-2 it was shown that the expected effects of education on wages were different for Americans of different races. The impacts ranged from a low of $4394 in extra wages per year of education for Black Americans aged 30 and over to a high of $5993 in extra wages per year of education for White Americans. Figure 11-10 shows how an interaction model can be used to examine the statistical significance of these interracial differences. Model 1 of Figure 11-10 includes three ANOVA variables for race (White is the reference group), the independent variable of interest (Education), and three interaction variables for Race x Education.

The main effect of Education in Model 1 is 5393, confirming that every additional year of education is associated with an increase of $5393 in annual wages for White Americans aged 30 and over. The three interaction effects are all negative, confirming that for all other races education increases wages less than it does for whites. For Asians, the interaction effect is small and not statistically significant: education raises wages for Asians at roughly the same rate as it does for Whites. While impact of each additional year of education is $5393 for Whites, it is 5393 - 96 = $5297 for Asians (the difference between this result and that reported in Figure 11-2 is due to rounding). The interaction effects for Blacks and Others are negative and statistically significant (in the case of Blacks, highly significant). This means that the effects of each extra year of education on wages are significantly lower for Blacks and Others than it is for Whites. One shortcoming of Model 1 is that (as with any ANOVA model) all of the group differences are examined relative to the reference group (in this case, Whites). So, for example, Model 1 tells us whether or not the slope for Others differs significantly from the slope for Whites (it does), but it doesn't tell us whether or not the slope for the slope for Others differs significantly from the slope for Blacks. In order to find the statistical significance of the differences in slope between Blacks and the other three races, a new model has to be estimated that uses Blacks as the reference group. This is done in Model 2, in which the same variables are organized in such a way as to highlight the significance of differences from Blacks considered as a reference group (rather than Whites). Since Model 2 contains the same information as Model 1, the R2 doesn't change from Model 1, but the coefficients (and their significance levels) do. In Model 2 of Figure 11-10, the main effect of Education is now 4394, consistent with the fact that Black is now the reference group and every additional year of education is associated with an extra $4394 in expected annual wages for Black Americans aged 30 and over. The coefficient for the White interaction is 999, indicating that Whites are expected to earn an extra 4394 + 999 = $5395 for each additional year of schooling, just as in Model 1. What Model 2 tells us that Model 1 does not is that the difference between the impact of education for Others versus Blacks ($28 per year of education) is not statistically significant. It also tells us that the difference in the returns to education for Asians versus Blacks ($904 per year of education) is statistically significant. Model 1 and Model 2 represent the same information, but by using different reference groups they allow the examination of the significance of different racial differences. The expected values of wages based on education for all four races are plotted in Figure 11-11. The values plotted in this graph could be calculated from either of the two regression models (or from the models reported in Figure 11-2) Notice how the slope for Whites is steeper than the slopes for the other three races. Among high school dropouts, Whites are expected to earn barely more than Others, but among people with post-graduate education, Whites are expected to earn almost as much as Asians. The differences in slopes between Asians and Whites on the one hand and Blacks and Others on the other mean that racial inequalities in American wages increase as education levels rise. Rising education levels in society are not likely to make American society more equal. Quite the contrary: they seem likely to make existing racial inequalities even worse.

11.5. Case study: Cross-national comparison of democracy ratings In Chapter 5 it was argued that older people in Taiwan might rate the quality of Taiwan's democracy more highly because older Taiwanese had lived through a period of dictatorship before 1991. This might be called the "dictatorship theory" of democracy ratings. It was suggested in Chapter 5 that younger people who came of age in the democratic era might be more demanding, and as a result be less satisfied with Taiwan's democracy than older people. A regression model confirmed this reasoning. Taiwanese people's ratings of the democratic quality of their government was found to rise with age. The fact that Taiwanese people's ratings of Taiwanese democracy rise with age tends to support the dictatorship theory, but it doesn't prove the theory. An alternative theory, the "youth theory," might be that young people everywhere are more demanding when it comes to democracy, while older people are less demanding. One way to shed light on the relative merits of the two theories would be to compare the relationship between age and democracy ratings in Taiwan to those in another country. For this purpose, the United States has been chosen as a reference country, since the United States has never experienced a period of dictatorship. As a reminder, people's ratings of democracy have been scored on a scale from 0 to 100 where: Rating = 0 means the respondent thinks there is not enough democracy in her or his country Rating = 50 means the respondent thinks there is just the right amount of democracy in her or his country Rating = 100 means the respondent thinks there is too much democracy in her or his country The mean democracy rating (for all ages) was 38.7 in Taiwan and 37.2 in the United States. Regression models reporting the relationship between age and democracy ratings for the United States and Taiwan are reported in Figure 11-12. The Taiwan model is identical to that reported in Figure 5-7, except that now we have significance levels and an R2 to work with in addition to just the coefficients. The increase in democracy ratings with age is, in fact, highly statistically significant. The United States model, on the other hand, shows that democracy ratings decline with age in the United States. The decline with age in the US is even stronger than the rise with age in Taiwan. This seems to support the dictatorship theory over the youth theory of democracy ratings.

A formal interaction model of the differences in the slope of the relationship between age and democracy ratings is reported in the final column of Figure 11-12. This model includes the independent variable of interest (Age), the ANOVA variable that distinguishes between the two groups (Country), and an interaction variable (Country x Age). The main effect of Age in the interaction model is -0.117, which is the effect of age on democracy ratings in the United States. The interaction effect for age is 0.222, indicating that the coefficient for Age in Taiwan is 0.222 points higher than the coefficient for Age in the United States. This difference in the slope of the relationship between age and democracy ratings is highly significant (probability < .001). The intercept effect (-8.680) is of no theoretical interest in this model, though it is used when computing expected values. Those expected values of democracy ratings for people of different age in Taiwan versus the United States are plotted in Figure 11-13. Obviously, democracy ratings rise with age in Taiwan, while they decline with age in the United States. This tends to confirm the dictatorship theory that older Taiwanese might think less highly of Taiwan's democracy had they not themselves experienced what life was like under a dictatorship. Whether the differences between Taiwan and the United States are due to this reason or some other reason, it is very clear that the relationship between age and democracy ratings is different in the two countries. There is a significant interaction between country and the effects of age on people's democracy ratings.

Chapter 11 Key Terms

Interaction effects are the coefficients of the interaction variables in an interaction model.
Interaction models are regression models that allow the slopes of some variables to differ for different categorical groups.
Interaction variables are variables created by multiplying an ANOVA variable by an independent variable of interest.
Intercept effects are the coefficients of the ANOVA variables in an interaction model.
Main effects are the coefficients of the independent variable of interest in an interaction model for the reference group.