Statistics/Distributions/Normal (Gaussian)

Normal Distribution

Probability density function The red curve is the standard normal distribution
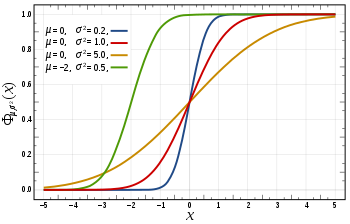
Cumulative distribution function
Notation	${\mathcal {N}}(\mu ,\,\sigma ^{2})$
Parameters	μ ∈ R — mean (location) σ2 > 0 — variance (squared scale)
Support	x ∈ R
PDF	${\frac {1}{\sigma {\sqrt {2\pi }}}}\,e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$
CDF	${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]$
Mean	μ
Median	μ
Mode	μ
Variance	$\sigma ^{2}\,$
Skewness	0
Ex. kurtosis	0
Entropy	${\frac {1}{2}}\ln(2\pi e\,\sigma ^{2})$
MGF	$\exp\{\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}\}$
CF	$\exp\{i\mu t-{\frac {1}{2}}\sigma ^{2}t^{2}\}$
Fisher information	${\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}$

Normal distribution is without exception the most widely used distribution. It also goes under the name Gaussian distribution. It assumes that the observations are closely clustered around the mean, μ, and this amount is decaying quickly as we go farther away from the mean. The measure of spread is quantified by the variance, $\sigma ^{2}$.

Some examples of applications are:

• If the average man is 175 cm tall with a variance of 6 cm, what is the probability that a man found at random will be 183 cm tall?
• If the average man is 175 cm tall with a variance of 6 cm and the average woman is 168 cm tall with a variance of 3cm, what is the probability that the average man will be shorter than the average woman?
• If cans are assumed to have a variance of 4 grams, what does the average weight need to be in order to ensure that the 99% of all cans have a weight of at least 250 grams?

The density function is:

$f_{\mu ,\sigma }(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}$

where $-\infty <x<\infty$.

and the cumulative distribution function cannot be integrated into a single expression.

Normal distribution with parameters μ and σ is denoted as $N(\mu ,\sigma )$. If the rv X is normally distributed with expectation μ and standard deviation σ, one denotes: $\!\,X\sim N(\mu ,\sigma )$

Probability mass function

To verify that f(x) is a valid pmf we must verify that (1) it is non-negative everywhere, and (2) that the total integral is equal to 1. The first is obvious, so we move on to verify the second.

$\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{\infty }e^{-(x-\mu )^{2}/2\sigma ^{2}}dx$

Now let $w={x-\mu \over \sigma {\sqrt {2}}}$. We see that $dw={dx \over \sigma {\sqrt {2}}}$.

${\frac {1}{\sqrt {\pi }}}\int _{-\infty }^{\infty }e^{-w^{2}}dw$

Now we use the Gaussian integral that $\int _{-\infty }^{\infty }e^{-w^{2}}\,dw={\sqrt {\pi }}$

${\frac {1}{\sqrt {\pi }}}{\sqrt {\pi }}=1$

Mean

We derive the mean as follows

$\operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot f(x)dx$

$=\int _{-\infty }^{\infty }x{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx$

$=\int _{-\infty }^{\infty }[(x-\mu )+\mu ]{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx$

$=\int _{-\infty }^{\infty }(x-\mu ){\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx+\int _{-\infty }^{\infty }\mu {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx$

$={\frac {1}{\sigma {\sqrt {2\pi }}}}(-\sigma ^{2})\int _{-\infty }^{\infty }{-x+\mu \over \sigma ^{2}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx+\mu \int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx$

We now see that the right integral is the complete integral over a normal pmf. This is therefore 1.

$\operatorname {E} [X]={\frac {1}{\sigma {\sqrt {2\pi }}}}(-\sigma ^{2})\left[e^{-(x-\mu )^{2}/2\sigma ^{2}}\right]_{-\infty }^{\infty }+\mu$

$={\frac {1}{\sigma {\sqrt {2\pi }}}}(-\sigma ^{2})[0-0]+\mu$

$=\mu$

Variance

$\operatorname {Var} (X)=\operatorname {E} [(X-{E}[X])^{2}]=\int _{-\infty }^{\infty }(x-\mu )^{2}\cdot f(x)dx=\int _{-\infty }^{\infty }(x-\mu )^{2}{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\cdot \left({\frac {x-\mu }{\sigma }}\right)^{2}}dx$

We let $w={x-\mu \over \sigma {\sqrt {2}}}$

$\operatorname {Var} (X)=\int _{-\infty }^{\infty }\sigma ^{2}2w^{2}{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-w^{2}}\sigma {\sqrt {2}}dw={\frac {2\sigma ^{2}}{\sqrt {\pi }}}\int _{-\infty }^{\infty }w\cdot we^{-w^{2}}dw$

We now use integration by parts with u=w and v=(-1/2)e^(-w^2)

$\operatorname {Var} (X)={\frac {2\sigma ^{2}}{\sqrt {\pi }}}\left(\left[w{-1 \over 2}e^{-w^{2}}\right]_{-\infty }^{\infty }-\int _{-\infty }^{\infty }{-1 \over 2}e^{-w^{2}}dw\right)$

We see that the bracketed term is zero by L'Hôpital's rule.

$\operatorname {Var} (X)={\frac {2\sigma ^{2}}{\sqrt {\pi }}}\left({1 \over 2}\int _{-\infty }^{\infty }e^{-w^{2}}dw\right)$

Now we use the Gaussian integral again

$\operatorname {Var} (X)={\frac {2\sigma ^{2}}{\sqrt {\pi }}}{1 \over 2}{\sqrt {\pi }}=\sigma ^{2}$

External links

• Interactive Normal (Gaussian) Distribution Web Applet (Java)