We will calculate the rate at which the fuzziness of a position probability distribution increases, in consequence of the fuzziness of the corresponding momentum, when there is no counterbalancing attraction (like that between the nucleus and the electron in atomic hydrogen).
Because it is easy to handle, we choose a Gaussian function

which has a bell-shaped graph. It defines a position probability distribution

If we normalize this distribution so that  then
then  and
and

We also have that

- the Fourier transform of
 is
is 
- this defines the momentum probability distribution

- and

The fuzziness of the position and of the momentum of a particle associated with  is therefore the minimum allowed by the "uncertainty" relation:
is therefore the minimum allowed by the "uncertainty" relation: 
Now recall that

where  This has the Fourier transform
This has the Fourier transform
![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
and this defines the position probability distribution
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)
Comparison with  reveals that
reveals that  Therefore,
Therefore,
![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)
The graphs below illustrate how rapidly the fuzziness of a particle the mass of an electron grows, when compared to an object the mass of a  molecule or a peanut. Here we see one reason, though by no means the only one, why for all intents and purposes "once sharp, always sharp" is true of the positions of macroscopic objects.
molecule or a peanut. Here we see one reason, though by no means the only one, why for all intents and purposes "once sharp, always sharp" is true of the positions of macroscopic objects.
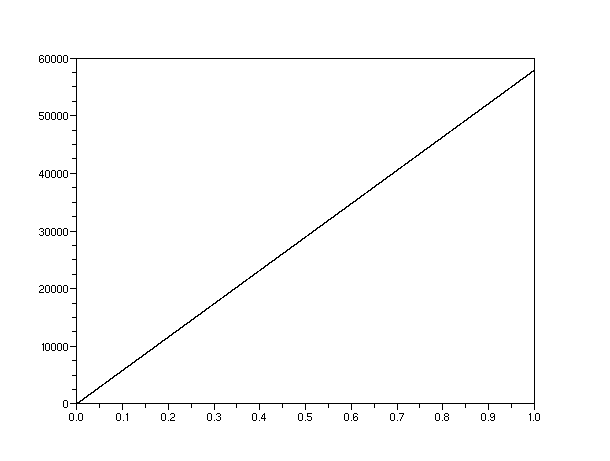
Above: an electron with  nanometer. In a second,
nanometer. In a second,  grows to nearly 60 km.
grows to nearly 60 km.
Below: an electron with  centimeter.
centimeter.  grows only 16% in a second.
grows only 16% in a second.

Next, a  molecule with
molecule with  nanometer. In a second,
nanometer. In a second,  grows to 4.4 centimeters.
grows to 4.4 centimeters.

Finally, a peanut (2.8 g) with  nanometer.
nanometer.  takes the present age of the universe to grow to 7.5 micrometers.
takes the present age of the universe to grow to 7.5 micrometers.















![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)


![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)






