The Intermediate Value Theorem is a fundamental theorem in calculus. The theorem states that if a function,
f
(
x
)
{\displaystyle f(x)}
[
a
,
b
]
,
{\displaystyle [a,b],}
y
{\displaystyle y}
(
f
(
a
)
{\displaystyle (f(a)}
f
(
b
)
,
{\displaystyle f(b),}
c
∈
(
a
,
b
)
{\displaystyle c\in (a,b)}
f
(
c
)
=
y
{\displaystyle f(c)=y}
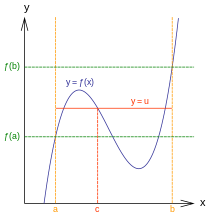
Intermediate Value Theorem: f(x) is continuous on [a, b], there exists at least one value c, that is defined on (a, b) such that f(c) = y. Statement: If a function,
f
{\displaystyle f}
[
a
,
b
]
,
{\displaystyle [a,b],}
y
{\displaystyle y}
f
(
a
)
{\displaystyle f(a)}
f
(
b
)
,
{\displaystyle f(b),}
c
∈
(
a
,
b
)
{\displaystyle c\in (a,b)}
f
(
c
)
=
y
{\displaystyle f(c)=y}
Proof: Assume that
f
(
x
)
{\displaystyle f(x)}
[
a
,
b
]
{\displaystyle [a,b]}
f
(
a
)
<
f
(
b
)
.
{\displaystyle f(a)<f(b).}
Consider a function
g
(
x
)
=
f
(
x
)
−
y
.
{\displaystyle g(x)=f(x)-y.}
g
(
x
)
{\displaystyle g(x)}
f
(
x
)
{\displaystyle f(x)}
y
{\displaystyle y}
Since
f
{\displaystyle f}
[
a
,
b
]
{\displaystyle [a,b]}
y
{\displaystyle y}
g
(
x
)
=
f
(
x
)
−
y
{\displaystyle g(x)=f(x)-y}
[
a
,
b
]
,
{\displaystyle [a,b],}
Now,
f
(
a
)
<
y
{\displaystyle f(a)<y}
c
∈
(
a
,
b
)
{\displaystyle c\in (a,b)}
y
=
f
(
c
)
{\displaystyle y=f(c)}
Or,
f
(
a
)
−
y
<
0
{\displaystyle f(a)-y<0}
∴
g
(
a
)
<
0
{\displaystyle \therefore g(a)<0}
In the same way,
g
(
b
)
>
0
{\displaystyle g(b)>0}
Since
g
(
x
)
{\displaystyle g(x)}
g
(
a
)
{\displaystyle g(a)}
x
{\displaystyle x}
g
(
b
)
{\displaystyle g(b)}
x
{\displaystyle x}
c
{\displaystyle c}
[
a
,
b
]
{\displaystyle [a,b]}
g
(
c
)
=
0
{\displaystyle g(c)=0}
Therefore, at the point
c
{\displaystyle c}
g
(
c
)
=
f
(
c
)
−
y
=
0
⟹
f
(
c
)
=
y
{\displaystyle g(c)=f(c)-y=0\implies f(c)=y}
∴ There exists at least one point
c
{\displaystyle c}
[
a
,
b
]
{\displaystyle [a,b]}
f
(
c
)
=
y
.
{\displaystyle f(c)=y.}
[Proved]


![{\displaystyle [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842)







![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)















