Topology/Vector Spaces
A vector space is formed by scalar multiples of vectors. The scalars are most commonly real numbers but can also be complex, or from any field.
Definition
[edit | edit source]A vector space on a field is a set equipped with two binary operations: common vector addition on elements of and scalar multiplication, by elements of on elements of . These operations are subject to 8 axioms (u,v, and w are vectors in and a and b are scalars in ):
1. Associativity (addition): (u+v)+w = u+(v+w).
2. Associativity (scalar and field multiplication): a(bu) = (ab)u
3. Distributivity (field addition): (a+b)u = au+bu
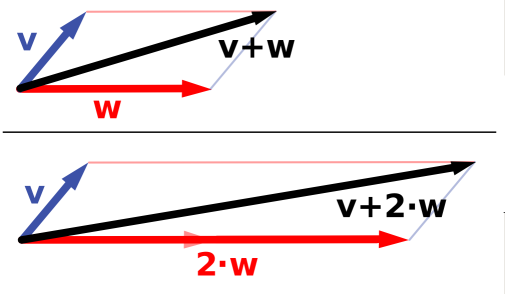
4. Distributivity (vector addition): a(u+v) = au+av
5. Identity element (addition): 0 such that u+0 = u u
6. Identity element (scalar multiplication): 1u = u
7. Commutativity: u+v = v+u
8. Inverse element: -u such that u+(-u) = 0 u