From Wikibooks, open books for an open world
Which of the following are vector quantities?
1.
4 miles northwest
2.
5 meters
3.
1200 people
4.
10 kilograms
5.
Pulling a cord straight down with a pressure of 10 pounds
6.
$200
Given
A
B
→
{\displaystyle {\overrightarrow {AB}}}
C
D
→
{\displaystyle {\overrightarrow {CD}}}
E
F
→
{\displaystyle {\overrightarrow {EF}}}
7.
G
H
→
=
A
B
→
{\displaystyle {\overrightarrow {GH}}={\overrightarrow {AB}}}
8.
I
J
→
=
−
A
B
→
{\displaystyle {\overrightarrow {IJ}}=-{\overrightarrow {AB}}}
9.
K
L
→
=
C
D
→
{\displaystyle {\overrightarrow {KL}}={\overrightarrow {CD}}}
10.
−
M
N
→
=
C
D
→
{\displaystyle -{\overrightarrow {MN}}={\overrightarrow {CD}}}
11.
O
P
→
=
−
E
F
→
{\displaystyle {\overrightarrow {OP}}=-{\overrightarrow {EF}}}
12.
Q
R
→
=
E
F
→
{\displaystyle {\overrightarrow {QR}}={\overrightarrow {EF}}}
Given the rectangle
A
B
C
D
{\displaystyle ABCD}
13.
A
D
→
=
B
C
→
{\displaystyle {\overrightarrow {AD}}={\overrightarrow {BC}}}
14.
O
D
→
=
−
B
O
→
{\displaystyle {\overrightarrow {OD}}=-{\overrightarrow {BO}}}
15.
A
B
→
=
C
D
→
{\displaystyle {\overrightarrow {AB}}={\overrightarrow {CD}}}
16.
A
O
→
=
−
O
C
→
{\displaystyle {\overrightarrow {AO}}=-{\overrightarrow {OC}}}
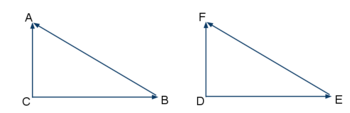
17. Using these two triangles we are given
C
A
→
=
D
F
→
{\displaystyle {\overrightarrow {CA}}={\overrightarrow {DF}}}
and
C
B
→
=
D
E
→
{\displaystyle {\overrightarrow {CB}}={\overrightarrow {DE}}}
Show that
B
A
→
=
E
F
→
{\displaystyle {\overrightarrow {BA}}={\overrightarrow {EF}}}
18.
Planes A , B , and C leave airport O at 8 A.M., plane A traveling N
60
∘
{\displaystyle 60^{\circ }}
B traveling due
north at 300 kilometers per hour, and plane C traveling southwest at 400 kilometers per hour. On paper or in drawing software, locate a point
representing the airport O . Through this point draw lines representing an east-west direction and a north-south direction, then sketch vectors
indicating the change in position of each of the first planes after the first hour of flight. Show correct scale by using 1 cm to represent 100 kilometers.
1.
Two forces, one of 300 N and the other of 200 N, act at a point on a body, and are perpendicular to each other.
Construct (on paper or using software) the vector representing the sum of the two forces.
2.
Construct the vector representing the sum of the two forces in Exercise 1 when the forces form an angle of
45
∘
{\displaystyle 45^{\circ }}
with each other.
3.
Two forces, one of 100 Newtons and one of 175 Newtons, act at a point on a body, and form an angle of
60
∘
{\displaystyle 60^{\circ }}
with each other. Construct the vector that represents the resultant of the two forces.
Various Vectors Using the vectors shown, construct:
4.
2
A
B
→
+
3
A
B
→
{\displaystyle 2{\overrightarrow {AB}}+3{\overrightarrow {AB}}}
5.
A
B
→
+
C
D
→
{\displaystyle {\overrightarrow {AB}}+{\overrightarrow {CD}}}
6.
2
(
A
B
→
+
C
D
→
)
{\displaystyle 2({\overrightarrow {AB}}+{\overrightarrow {CD}})}
7.
A
B
→
+
C
D
→
+
E
F
→
{\displaystyle {\overrightarrow {AB}}+{\overrightarrow {CD}}+{\overrightarrow {EF}}}
8.
A
B
→
+
C
D
→
+
E
F
→
+
G
H
→
{\displaystyle {\overrightarrow {AB}}+{\overrightarrow {CD}}+{\overrightarrow {EF}}+{\overrightarrow {GH}}}
Various Vectors Using the vectors shown, construct:
1.
A
B
→
−
E
F
→
{\displaystyle {\overrightarrow {AB}}-{\overrightarrow {EF}}}
2.
−
A
B
→
{\displaystyle -{\overrightarrow {AB}}}
3.
−
3
G
H
→
{\displaystyle -3{\overrightarrow {GH}}}
4.
E
F
→
−
A
B
→
{\displaystyle {\overrightarrow {EF}}-{\overrightarrow {AB}}}
5.
(
A
B
→
+
C
D
→
)
−
E
F
→
{\displaystyle ({\overrightarrow {AB}}+{\overrightarrow {CD}})-{\overrightarrow {EF}}}
Parallelogram ABCD Using parallelogram
A
B
C
D
{\displaystyle ABCD}
6.
A
C
→
−
A
B
→
=
?
{\displaystyle {\overrightarrow {AC}}-{\overrightarrow {AB}}=?}
7.
A
C
→
−
A
D
→
=
?
{\displaystyle {\overrightarrow {AC}}-{\overrightarrow {AD}}=?}
8.
A
B
→
=
−
?
{\displaystyle {\overrightarrow {AB}}=-?}