
The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:[1]

where  is the angle between sides
is the angle between sides  and
and  .
.
This formula had better agree with the Pythagorean Theorem when  .
.
So try it...
When  ,
, 
The  and the formula reduces to the usual Pythagorean theorem.
and the formula reduces to the usual Pythagorean theorem.
For any triangle with angles  and corresponding opposite side lengths
and corresponding opposite side lengths  , the Law of Cosines states that
, the Law of Cosines states that



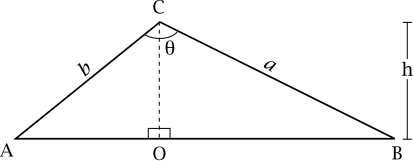
Dropping a perpendicular  from vertex
from vertex  to intersect
to intersect  (or
(or  extended) at
extended) at  splits this triangle into two right-angled triangles
splits this triangle into two right-angled triangles  and
and  , with altitude
, with altitude  from side
from side  .
.
First we will find the lengths of the other two sides of triangle  in terms of known quantities, using triangle
in terms of known quantities, using triangle  .
.

Side  is split into two segments, with total length
is split into two segments, with total length  .
.
 has length
has length 
 has length
has length 
Now we can use the Pythagorean Theorem to find  , since
, since  .
.

|

|
|
|

|
|
|

|
The corresponding expressions for  and
and  can be proved similarly.
can be proved similarly.
The formula can be rearranged:

and similarly for  and
and  .
.
This formula can be used to find the third side of a triangle if the other two sides and the angle between them are known. The rearranged formula can be used to find the angles of a triangle if all three sides are known. See Solving Triangles Given SAS.
- ↑
Lawrence S. Leff (2005-05-01). cited work. Barron's Educational Series. p. 326. ISBN 0764128922.



































