Trigonometric equations are equations including trigonometric functions. If they have only such functions and constants, then the solution involves finding an unknown which is an argument to a trigonometric function.
|
 |

|

|
![{\displaystyle {\begin{matrix}x=\alpha +2k\pi \\x=\pi -\alpha +2k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1a3e9f50511c58a1b5da92a54ebaa528586f4b0)
|

|

|

|

|

|

|

|

|
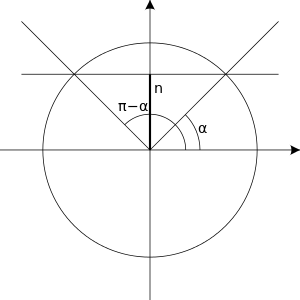
The equation  has solutions only when
has solutions only when  is within the interval
is within the interval ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) . If
. If  is within this interval, then we first find an
is within this interval, then we first find an  such that:
such that:

The solutions are then:


Where  is an integer.
is an integer.
In the cases when  equals 1, 0 or -1 these solutions have simpler forms which are summarized in the table on the right.
equals 1, 0 or -1 these solutions have simpler forms which are summarized in the table on the right.
For example, to solve:

First find  :
:

Then substitute in the formulae above:


Solving these linear equations for  gives the final answer:
gives the final answer:


Where  is an integer.
is an integer.

|
 |

|

|
![{\displaystyle {\begin{matrix}x=\pm \alpha +2k\pi \\\alpha \in [0,\pi ]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb327bcece984447ffb90d738e9f5c2246d7375d)
|

|

|

|

|

|

|

|

|
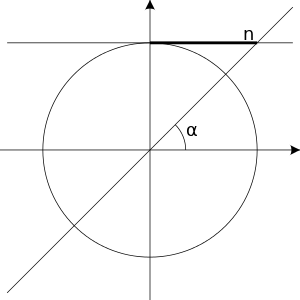
Like the sine equation, an equation of the form  only has solutions when n is in the interval
only has solutions when n is in the interval ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) . To solve such an equation we first find one angle
. To solve such an equation we first find one angle  such that:
such that:

Then the solutions for  are:
are:

Where  is an integer.
is an integer.
Simpler cases with  equal to 1, 0 or -1 are summarized in the table on the right.
equal to 1, 0 or -1 are summarized in the table on the right.

|
 |

|
General
case
|
![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091023c5ebe89e390dc7b3c08dc2aafd52f739cb)
|

|

|

|

|

|

|
An equation of the form  has solutions for any real
has solutions for any real  . To find them we must first find an angle
. To find them we must first find an angle  such that:
such that:

After finding  , the solutions for
, the solutions for  are:
are:

When  equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
|
 |

|
General
case
|
![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[0;\pi \right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a09654bc73208cf0114b0bbebf26b68271c20ad0)
|

|

|

|

|

|

|
The equation  has solutions for any real
has solutions for any real  . To find them we must first find an angle
. To find them we must first find an angle  such that:
such that:

After finding  , the solutions for
, the solutions for  are:
are:

When  equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
The trigonometric equations  and
and  can be solved by transforming them to other basic equations:
can be solved by transforming them to other basic equations:


Generally, to solve trigonometric equations we must first transform them to a basic trigonometric equation using the trigonometric identities. This sections lists some common examples.
To solve this equation we will use the identity:


The equation becomes:


This equation is of the form  and can be solved with the formulae given above.
and can be solved with the formulae given above.
For example we will solve:

In this case we have:



Apply the identity:


So using the formulae for  the solutions to the equation are:
the solutions to the equation are:


Where  is an integer.
is an integer.





![{\displaystyle {\begin{matrix}x=\alpha +2k\pi \\x=\pi -\alpha +2k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1a3e9f50511c58a1b5da92a54ebaa528586f4b0)








![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)














![{\displaystyle {\begin{matrix}x=\pm \alpha +2k\pi \\\alpha \in [0,\pi ]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb327bcece984447ffb90d738e9f5c2246d7375d)







![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091023c5ebe89e390dc7b3c08dc2aafd52f739cb)






![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[0;\pi \right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a09654bc73208cf0114b0bbebf26b68271c20ad0)

















