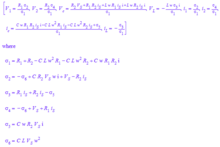From Wikibooks, open books for an open world
Complex 2R, L, C, voltage circuit Given that the voltage source is defined by
V
s
(
t
)
=
c
o
s
(
t
)
{\displaystyle V_{s}(t)=cos(t)}
I
s
(
t
)
=
2
s
i
n
(
t
−
p
i
3
)
{\displaystyle I_{s}(t)=2sin(t-{\frac {pi}{3}})}
Circuit marked up for analysis The values of capacitor, inductor, and
ω
{\displaystyle \omega }
Knowns:
V
s
,
R
1
,
R
2
,
L
,
C
,
I
s
{\displaystyle V_{s},R_{1},R_{2},L,C,I_{s}}
Unknowns:
v
1
,
v
2
,
v
C
,
v
L
,
i
1
,
i
2
,
i
C
,
i
L
{\displaystyle v_{1},v_{2},v_{C},v_{L},i_{1},i_{2},i_{C},i_{L}}
Equations:
v
1
=
R
1
∗
i
1
{\displaystyle v_{1}=R_{1}*i_{1}}
v
2
=
R
2
∗
i
2
{\displaystyle v_{2}=R_{2}*i_{2}}
i
C
=
C
∗
d
d
t
v
C
{\displaystyle i_{C}=C*{d \over dt}v_{C}}
v
L
=
L
∗
d
d
t
i
L
{\displaystyle v_{L}=L*{d \over dt}i_{L}}
i
1
+
I
s
−
i
2
−
i
C
=
0
{\displaystyle i_{1}+I_{s}-i_{2}-i_{C}=0}
i
c
−
I
s
−
i
L
=
0
{\displaystyle i_{c}-I_{s}-i_{L}=0}
v
1
+
v
2
−
V
s
=
0
{\displaystyle v_{1}+v_{2}-V_{s}=0}
v
C
+
v
L
−
v
2
=
0
{\displaystyle v_{C}+v_{L}-v_{2}=0}
Can not substitute and get one differential equation. Must solve all equations simultaneously.
mupad symbolic solution .. code mupad numeric solution .. code Can solve simultaneous linear equations in the phasor domain ... so must convert them to phasor domain:
V
s
(
t
)
→
V
s
=
1
{\displaystyle {V_{s}}(t)\rightarrow {\mathbb {V} _{s}}=1}
I
s
(
t
)
→
I
s
=
−
2
∗
s
i
n
(
π
3
)
−
j
∗
2
∗
c
o
s
(
π
3
)
=
−
1.7321
−
j
{\displaystyle {I_{s}}(t)\rightarrow {\mathbb {I} _{s}}=-2*sin({\frac {\pi }{3}})-j*2*cos({\frac {\pi }{3}})=-1.7321-j}
i
1
→
I
1
{\displaystyle i_{1}\rightarrow \mathbb {I} _{1}}
i
2
→
I
2
{\displaystyle i_{2}\rightarrow \mathbb {I} _{2}}
i
C
→
I
C
{\displaystyle i_{C}\rightarrow \mathbb {I} _{C}}
i
L
→
I
L
{\displaystyle i_{L}\rightarrow \mathbb {I} _{L}}
v
1
→
V
1
{\displaystyle v_{1}\rightarrow {\mathbb {V} _{1}}}
v
2
→
V
2
{\displaystyle v_{2}\rightarrow {\mathbb {V} _{2}}}
v
C
→
V
C
{\displaystyle v_{C}\rightarrow {\mathbb {V} _{C}}}
v
L
→
V
L
{\displaystyle v_{L}\rightarrow {\mathbb {V} _{L}}}
now transform the calculus operations into the phasor domain ..
d
d
t
i
→
j
ω
I
{\displaystyle {d \over dt}i\rightarrow j\omega \mathbb {I} }
d
d
t
v
(
t
)
→
j
ω
V
{\displaystyle {d \over dt}v(t)\rightarrow j\omega \mathbb {V} }
So:
V
1
=
R
1
∗
I
1
{\displaystyle \mathbb {V} _{1}=R_{1}*\mathbb {I} _{1}}
V
2
=
R
2
∗
I
2
{\displaystyle \mathbb {V} _{2}=R_{2}*\mathbb {I} _{2}}
I
C
=
C
∗
j
ω
V
C
{\displaystyle \mathbb {I} _{C}=C*j\omega \mathbb {V} _{C}}
V
L
=
L
∗
j
ω
I
L
{\displaystyle \mathbb {V} _{L}=L*j\omega \mathbb {I} _{L}}
I
1
+
I
s
−
I
2
−
I
C
=
0
{\displaystyle \mathbb {I} _{1}+\mathbb {I} _{s}-\mathbb {I} _{2}-\mathbb {I} _{C}=0}
I
c
−
I
s
−
I
L
=
0
{\displaystyle \mathbb {I} _{c}-\mathbb {I} _{s}-\mathbb {I} _{L}=0}
V
1
+
V
2
−
V
S
=
0
{\displaystyle \mathbb {V} _{1}+\mathbb {V} _{2}-\mathbb {V} _{S}=0}
V
c
+
V
L
−
V
2
=
0
{\displaystyle \mathbb {V} _{c}+\mathbb {V} _{L}-\mathbb {V} _{2}=0}
The symbolic solution is too complicated to mark up in wiki, but can be seen in a screen shot. Translating this into the time domain symbolically is doubles the complexity (and mistakes).
The numeric solution is:
variable
real
imaginary
magnitude
angle
v1
2
-1.73j
2.644
∠ -0.7131
v2
-1
1.73j
1,9982
∠ 2.0949
vC
-3.598
- 0.76795j
3.6789
∠ -2.9313
VL
2.598
2.5j
3.6055
∠ 0.7662
i1
2
- 1.73j
2.644
∠ -0.7131
i2
-0.5
0.866j
1
∠ 2.0944
iC
0.76785
- 3.598j
3.679
∠ -1.3605
iL
2.5
- 2.598j
3.6055
∠ - 0.8046