Engineering Acoustics/Anechoic Tiling

Introduction

HMS Triumph (S93) anechoic tiling.

One important application of acoustics research is the testing, design, and construction of anechoic tiles for underwater acoustic stealth. Anechoic tiling, first used in the Second World War by German U-boats (codenamed “Alberich” ), are used to reduce the acoustic signature of naval vessels. The tiles reduce both reflected active SONAR off the pressure hull, and reduce internal noise transmitted through the pressure hull that can be picked up by passive SONAR. In modern times, anechoic tiles are present on nearly all submarines. The frequency range of SONAR, and consequently the range of interest of anechoic tiling to minimize detection, is around 1-30 kHz .

The main sound attenuation mechanism in the tiles comes from resonant scattering the sound waves due to air cavities in the rubber. The use of air bubbles to attenuate sound was first published by German acousticians Erwin Meyer and Eugen Skudrzyk in a report written in the British occupied zone of Germany in 1946, translated to English in 1950 for an unclassified release by the U.S. Navy . The air bubbles work to attenuate sound by acting as resonant oscillators and dissipate acoustic energy through thermal losses, frictional losses, and other processes.

Tank measurements of acoustic parameters with the panel surround on both sides by water, or “free-field”, are theoretically simple measurements that can be conducted in an interior laboratory setting , and will be described in later sections. Audoly presents a method to transfer the results of free-field acoustic properties from tank acoustic measurements to the acoustic properties of panels with arbitrary backing, such as the rigid backing of a submarine hull.

Planar Waves

The transmission and reflection coefficients ${\hat {T}}$ and ${\hat {R}}$ are presented as ratios of the incident, reflected, and transmitted acoustic pressure magnitudes:

${\hat {T}}={\frac {{\hat {P}}_{transmitted}}{{\hat {P}}_{incident}}},\quad \quad {\hat {R}}={\frac {{\hat {P}}_{reflected}}{{\hat {P}}_{incident}}}$

(1)

The conservation of acoustic power from transmitted waves through a panel is as follows: $|{\hat {T}}|^{2}+|{\hat {R}}|^{2}+|{\hat {A}}|^{2}=1$

Where ${\hat {A}}$ is the acoustic absorption coefficient. From careful observation of the conservation of energy equation, it is evident that to minimize $|{\hat {T}}|$ and $|{\hat {R}}|$, acoustic energy dissipated $|{\hat {A}}|$ should be increased. In materials such as metals in the frequency ranges pertinent to this study, $|{\hat {A}}|\approx 0$. In rubber materials, and especially those with air voids , $|{\hat {A}}|$ can no longer be assumed to be negligible .

The terms "insertion loss" ($IL$) or "echo reduction" ($ER$) are used. The insertion loss is the reduction (in decibels) of the acoustic power of the insertion of a panel, related to the transmission coefficient: $IL=-10\log |{\hat {T}}|^{2}$, and the echo reduction is the reduction (in decibels) of the acoustic power after a reflection: $ER=-10\log |{\hat {R}}|^{2}$.

Three-layered media: No panel absorption

For three-layered medium with two infinite fluid layers, each with impedance $r_{1/3}=\rho _{1/3}c_{1/3}$ on either side of a sample of thickness $L$ and impedance impedance $r_{2}=\rho _{2}c_{2}$, and $k=\omega /c_{2}$, at normal incidence the following equation for the reflection coefficient ${\hat {R}}$ may be used :

${\hat {R}}={\frac {(1-r_{1}/r_{3})\cos kL+j(r_{2}/r_{3}-r_{1}/r_{2})\sin kL}{(1+r_{1}/r_{3})\cos kL+j(r_{2}/r_{3}+r_{1}/r_{2})\sin kL}}$

(2)

For the symmetrical case of the first fluid and third fluid identical $r_{3}=r_{1}$, equation (2) can be reduced into the following simplified formulations :

$IL=10\log \left[1+{\frac {(1-m^{2})^{2}}{4m^{2}}}\sin ^{2}kL\right],\quad ER=10\log \left[1+{\frac {4m^{2}}{(1-m^{2})^{2}\sin ^{2}kL}}\right]$

(3)

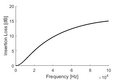
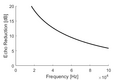
Where $m={\frac {r_{1}}{r_{2}}}$. By inspection of equations (3), resonances of minima of ${\hat {R}}$ and maxima of ${\hat {T}}$ occur at $kL=n\pi$. These lossless $IL$ and $ER$ are plotted over $kL$ in the following figures in the next section (for aluminum panels suspended in water) as the black lines.

Three-layered media: With panel absorption

For panel media with acoustic attenuation, the following formulas in (4) can be used to describe the insertion loss and echo reduction, where $\alpha$ is the attenuation constant in $dB/m$, and $r={\frac {\alpha }{\omega c_{2}}}$. For the case of no acoustic attenuation $\alpha =0$, equations (3) are recovered.

$IL=20\log \left|{\frac {(m+1-jr)^{2}\exp(2jkL)-(m-1+jr)^{2}\exp(-2\alpha L)}{4m(1-jr)\exp(jkL-\alpha L)}}\right|,\quad \quad ER=20\log \left|{\frac {{\frac {m+1-jr}{m-1+jr}}\exp(jkL+\alpha L)-{\frac {m-1+jr}{m+1-jr}}\exp(-jkL-\alpha L)}{\exp(jkL+\alpha L)-\exp(-jkL-\alpha L)}}\right|$

(4)

A sketch of the effect of absorption in panel materials on $IL$ and $ER$ is shown in the following figures:

Images IL/ER IL plot showing the effect of increased absorption ER plot showing the effect of increased absorption

For a general formulation of n-layer solid panels with absorption, methods are described in references .

Determination of α(ω) from experimental data

A 2nd order approximation for $\alpha$ is used (Equation (5)) as it is not constant over frequency , as shown for the case of aluminum and nitrile rubber in the figure below.

$\alpha (\omega )\approx a\omega +b\omega ^{2}$

(5)

Images α(ω) Approximate attenuation coefficients α(ω) for 7075 Aluminum Alloy and Nitrile Butadiene Rubber (NBR)

It is possible to experimentally determine $\alpha (\omega )$ from tank acoustic tests. First the magnitude of the absorption coefficient is determined from conservation of energy and measured values of $|{\hat {T}}|$ and $|{\hat {R}}|$ :

$|{\hat {A}}|={\sqrt[{}]{1-|{\hat {T}}|^{2}-|{\hat {R}}|^{2}}}$

(6)

The coefficient $a$ in equation (5) is estimated using the following formula, then $b$ is then fit to data .

$a={\frac {|{\hat {A}}|}{\omega L}}$

(7)

Experimental Investigations

To characterize $|{\hat {T}}|$ and$|{\hat {R}}|$ of panel materials, free field acoustic measurements are performed: In a water-filled tank, a parametric array source $(a)$ produces an highly directional discrete acoustic wave with the far-field directionality function $D(\theta )$ . For demonstration, the far field directionality of an underwater array source is included in the insertion loss sample measurement figure below. The shape of the discrete wave is shown in .

$D(\theta )={\frac {2J_{1}(ka\sin \theta )}{ka\sin \theta }}$

(8)

Insertion Loss

Using a hydrophone $(c)$, one recording is made with the sample $(b)$ in place to record transmitted pressure $P_{t}$ and one measurement without the sample in place to record incident pressure $P_{i}$. The measurement configurations are shown in the following figures.

Images IL Insertion Loss Sample Experiment of Aluminum Plate Insertion Loss Reference Experiment of Aluminum Plate

Echo Reduction

For reflection experiments, the reflected pressure $P_{r}$ off the sample is measured, and for the incident pressure $P_{i}$ measurement a foam reflector is used. A foam reflector has a high acoustic impedance mismatch with the water and reflects sound efficiently.

Images ER Echo Reduction Sample Experiment of Aluminum Plate Echo Reduction Reference Experiment

Pressure Measurements

Shown in the following figures, the measured pressure signals over time are are recorded and processed with a Fourier transform to determine pressure over frequency. The coefficients $|{\hat {R}}|$ and $|{\hat {T}}|$ over frequency are simply the ratio of the resultant pressure spectra.

Images Pressure Representative pressure measurement Representative FFT analysis

Results

Insertion loss and echo reduction plots for, aluminum test samples, such as those measured in , are shown in the following figures. Aluminum samples are conducted as it is a material with well known acoustic properties, and negligibly low absorption over the frequencies studied. The experimental setup described shows good agreement with theory .

Images Aluminum_plate Predicted Insertion Loss of 13 mm Aluminum Plate Predicted Echo Reduction of 1 mm Aluminum Plate

Other Considerations

For applications of anechoic tiling on submarines, the conditions surrounding the submarine change drastically with submerged depth. Varying pressure, salinity, temperature all affect acoustic properties of the rubber, the surrounding water, and the anechoic tile in general. Environmental tank such as the ones described in reference can be used to simulate ocean conditions. The wavelength of the sound produced by the parametric array is limited by the physical size of the tank. Achieving lower frequency measurements necessitates the use of larger tanks for experiments, or semi-anechoic siding on the tank walls .

References

Back to main page

---

By: Geoffrey Chase